智能水滴算法求解TSP问题的研究
2015-06-24丁海军
赵 莉,丁海军
(河海大学常州校区 物联网工程学院,江苏 常州 213022)
智能水滴算法求解TSP问题的研究
赵 莉,丁海军
(河海大学常州校区 物联网工程学院,江苏 常州 213022)
智能水滴算法是一种模拟自然界中河水和河床相互作用的算法,根据智能水滴算法易于收敛于局部最优解,通过设置路径间最大、最小泥土量对算法进行改进,实现了水滴优化算法,并且将其运用到TSP(旅行商问题)的求解中.并对TSP51、TSP76问题进行仿真分析,结果表明改进的水滴群算法比原智能水滴算法具有更好的求最优解的能力,收敛速度更快,效果更好.
智能水滴算法;旅行商问题;最优解
智能水滴算法(IDW)是2007年由Shah-Hosseini[1]首先提出来的,这个算法是由模仿自然界水系统和其周围环境的相互作用而形成河道的过程进行迭代运算,最后得到优化的结果.它提供了一种新的解决方案来解决NP难的问题.目前,智能水滴算法已经被用于机器人路径规划[2],n皇后问题[3],多维背包问题 (MKP)[4]等一系列复杂优化问题中,并取得了较好的实验结果.与已有的智能算法相比,如蚁群算法[6]、蜂群算法[7]、遗传算法[8]等,智能水滴算法在解决复杂优化问题中具有一定的优势,这表明智能水滴算法是一种具有发展前景的算法.
1 智能水滴
在自然界中,流动的水滴和河道之间的关系是通过作用力与反作用力形成的.无数的流动的水滴形成了一个非常大的流动群体,所以就创造了河流流经的河道.流动的水滴一般具有2个基本的属性:水滴前行的速度velocity(IWD),水滴当中携带的泥土含量soil(IWD).当一个水滴点流动到其下方另外一点时,水滴的前行速度会变大,水滴自身携带的泥土含量会变多,在2个节点之间的河床上的泥土含量会变少.
对于每一个水滴来说,2个基本的属性velocity和soil在水滴流动的过程中会发生变化,水滴流动的周围环境就表示需要解决的问题,而智能水滴的作用其实就是为这些需要解决的问题找到一条最短的路径.
2 智能水滴算法的TSP求解
TSP(旅行商问题)的目标是在给定地图上城市间所有可能行程中找到一条总长度最短的行程.假设G=(C,L)是一个有向完全图,TSP的目标是从有向完全图G中找出一条长度最短的路径,即一条对C={c1,c2,…,cn}中n个城市访问且访问一次的最短的封闭曲线.
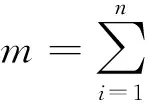
2.1 边缘选择机制
当第k个水滴在节点i时,选择下一个节点j的概率如下:
(1)
其中:ηij=1/dij,dij为城市i和城市j之间的距离,ηij表示路径(i,j)上的泥土量的启发式因子.α是路径中的泥土量在指导水滴群搜索中的相对重要度,其值越大,路径中的泥土量在水滴选择下一个要到的城市中起到的作用越大.β是水滴在流动过程中路径长度信息在指导水滴群搜索中的相对重要性,其值越大,启发式因子在水滴群选择下一个城市时所起到的作用越大.
f是与路径中泥土量相关的函数:

(2)
其中常数εs是一个非常小的正数,通常取值为0.01.用来防止函数f的分母为0,函数g用来确保将位置i与位置j之间的路径泥土量转换为正数,其表达式为:
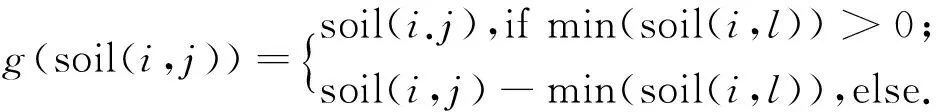
(3)
其中函数min用来得到当前位置与所有可能的下一个位置之间的泥土量的最小值.
2.2 更新当前的动能和泥土含量
第k个水滴在t+1时刻从点i移动到下一点j的动能变换为vk(t+1):

(4)
其中av,bv,cv是用户选定的大于0的静态参数,路径上的泥土量soil(i,j)和第k个水滴中的泥土量都是由Δsoil(i,j)来更新的.
Δsoil(i,j)是指路径中被移除的泥土量或是水滴中携带的泥土量,其中Δsoil(i,j)非线性正比于vIWDK的倒数:
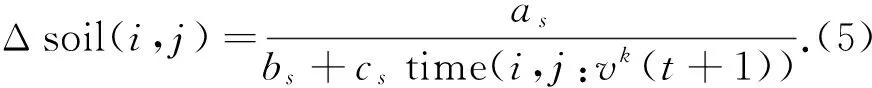
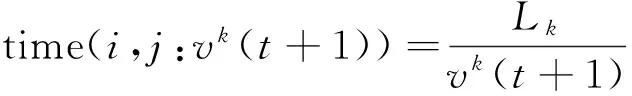
(6)
Lk表示第k个水滴走过的路径长度.
水滴从节点i移动到j路径中的泥土量和水滴中含有的泥土量更新如下:
soil(i,j)=(1-ρn)soil(i,j)-ρnΔsoil(i,j).
(7)
soilIWDk=soilIWDk+Δsoil(i,j).
(8)
其中ρn通常取值0.9.
2.3 全局的泥土量更新
在每一次的IWD算法迭代结束后,对于一条迭代最优的解决方法更新它的全局路径中的泥土量:
soil(i,j)=(1+ρIWD)·soil(i,j)-
ρIWD·1/(NIB-1)·soilIWD.
(9)
其中ρIWD是全局泥土量更新参数,通常取值0.9.NIB是此次迭代中节点的数目.
3 改进的智能水滴算法
由于路径中的泥土含量随着水滴的移动是不断变化的,因此在算法搜索陷入局部最优时,若某段路径弧段的泥土含量的数量比其他的路径上的泥土含量的数量多得多的时候,会导致算法提早进入收敛状况,针对这一不足点,文章通过借助MMAS思想,对各个路径上的泥土量实施了最大和最小量的限制,即:
smin≤sij(t)≤smax.
式中:smin,smax分别表示各边泥土量的最大值,最小值.按照文献[5]中的渐进估计方法,smin和smax取值如下:
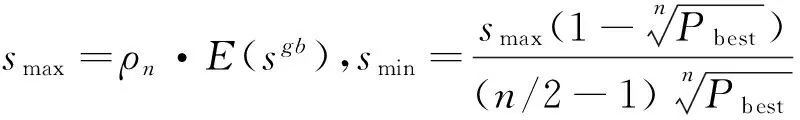
(10)
其中Pbest在本文中取为0.5,n为城市的数目,E(sgb)是目前为止找到的最短解.
在每一次循环后,必须确保泥土量sij(t)遵循这一限制条件,若有sij(t)>smax,则设置sij(t)=smax;若sij(t) 算法具体步骤如下: 1) 初始化算法中的各个参数,开始时,循环次数iterc为0,并设置最大循环次数itercmax,并将m个水滴置于n个城市上; 2) 当iterc≤itercmax时,iterc向上加1,并转到步骤3),否则,跳转到步骤8); 3) 对水滴的禁忌表索引号k=1; 4) 水滴依据状态转移概率公式计算得到概率选择城市j来前进,j∈{C-tabuk}; 5) 修改禁忌表,并将水滴转移到新的城市,把新城市转移到水滴的禁忌表中; 6) 对于每一个从节点i移动到节点j的水滴,更新其动能并计算泥土量.并转到4); 7)当所有城市遍历完,并找到一条迭代最优的路径,更新全局的泥土量,清空禁忌表且转到步骤2); 8) 输出最终结果. 为了验证算法的有效性,算法由Java语言实现,并在Javascript环境下编译,在不同的TSP问题上进行验证,在所有的实验中设置静态参数av,bv,cv和as,bs,cs分别为1,0.1,1.节点i和节点j之间的泥土量初始化sinit=1 000.每一个水滴的动能初始为vinit=200.α=0.4,β=0.8.水滴的数目m和城市的数目相等,最大迭代次数为 1 000,每个程序运行50次. 表1 TSP51问题实验仿真结果 表2 TSP76问题实验仿真结果 由上述的实验结果可知,改进的智能水滴算法在对各个路径上的泥土量进行了最大最小的限制以后,由表1、2的结果在最佳路径长度上较基本的智能水滴算法略优,在运行时间上,也占有一定的优势,这是因为通过对路径上的泥土量设置上下限,能够降低算法的时间复杂度,避免算法出现停滞.由图1、2可知,改进的智能水滴算法比基本的智能水滴算法在收敛速度及寻找最优解方面更加有效,进一步加强了该算法求最优解的能力,防止算法陷入局部最优. 研究结果表明,改进的智能水滴算法在对路径中的泥土含量进行了限制以后,提高了算法的收敛速度,有效地防止算法陷入局部最优解,该改进算法能够在迭代次数较少的情况下,较基本的智能水滴算法更能找到一条最优解.但是智能水滴算法参数较多,设置的值不同可能会导致该算法的效率不同,如何有效设置参数,提升算法的效率与精度,这是今后的研究方向. [1] SHAH-HOSSEINI H.Problem solving by intelligent water drops[C]//Evolutionary Computation,2007.IEEE,2007:3226-3231. [2] DUAN H,LIU S,LEI X.Air robot path planning based on intelligent water drops optimization[C]//Neural Networks,2008.IEEE,2008:1397-1401. [3] 刘娟,欧阳建权,陈良军.用混合遗传算法求解n皇后问题[J].湘潭大学学报:自然科学版,2007,29(2):37-41. [4] SHAH-HOSSEINI H.Optimization with the nature-inspired intelligent water drops algorithm [J].Evolutionary Computation,2009:297-320. [5] EBERHART R C,KENNEDY J.A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science.1995(1):39-43. [6] DORIGO M,GAMBARDELLA L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].Evolutionary Computation,IEEE Transactions on,1997,1(1):53-66. [7] WONG L P,LOW M Y H,CHONG C S.A bee colony optimization algorithm for traveling salesman problem[C]//Proceedings of the 2008 Second Asia International Conference on Modelling & Simulation (AMS).IEEE Computer Society,2008:818-823.[8] GREFENSTETTE J,GOPAL R,ROSMAITA B,et al.Genetic algorithms for the traveling salesman problem[C]//Proceedings of the first International Conference on Genetic Algorithms and their Applications.New Jersey:Lawrence Erlbaum,1985:160-168. (责任编辑 庄红林) Intelligent water drops algorithm for solving TSP ZHAO Li,DING Hai-jun (1.College of Internet of Things Engineering,Hohai University at Changzhou,Changzhou 213022,China) Intelligent water drops algorithm is a meta-heuristic method that imitates some natural phenomena of a swarm of water drops with the soil onto the river-bed.Because it is easy to converge to a local optimal solution, this paper gives an improved algorithm by setting the maximum and minimum amount of soil on the path. The paper applies it to the Traveling Salesman Problem (TSP), and gives a simulation analysis of TSP51 and TSP76 problems. The experimental results show that theis improved water drops algorithm is better than the previous one. intelligent water drops algorithm;TSP;optimal solution 2014-06-03. 赵莉(1990-),女,硕士研究生.主要研究方向:数据挖掘. 丁海军(1963-),男,硕士,副教授,硕士生导师.主要研究方向:数据挖掘. TN929.5 A 1672-8513(2015)01-0062-044 实验结果与分析


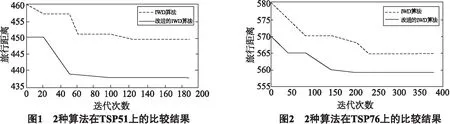
5 结语

