构造法在中学数学解题中的应用点滴体会
2015-06-23湖南省汉寿县第二中学
湖南省汉寿县第二中学 王 飞
构造法是指某些数学问题用通常办法难以解决时,根据题目所给条件和结论的特征、性质,从新的角度,用新的观点观察分析、解释对象,抓住反映问题的条件与结论之间的内在联系,用已知的数学关系为支架构造出满足条件或结论的数学对象,使原问题中隐晦不清的关系和性质在新构造的数学对象中清楚的表现出来,从而借助该数学对象解决数学问题的方法。
一、构造法的解题思路
构造法解题的基本思想方法是转化思想,用构造法解题的巧妙之处在于不是直接解决所给问题,而是把它转化为与原问题有关的辅助新问题,然后通过新问题的解决帮助解决原问题。
二、构造法的解题模式
构造法的内涵十分丰富,解题也没有一个绝对统一的模式。它需要更多的分析、类比、归纳和判断,同时能激发人们的思维。如何借助构造法实现解题过程的转化呢?关键是对题设条件进行逻辑处理,通过一般的特殊化的想象,巧妙地对问题分析与综合,构造出一种思维的创造物或想象物。构造法解题过程的大致模式和步骤如下:一是对题设条件特征的分析;二是通过创新思维进行转化;三是构造方程、数列、函数(或图像)、关系式;四是通过推演实现转化;五是结论。
三、构造法在中学数学解题中的应用举例
1.构造方程法
方程,作为中学数学重要的知识之一,与数、式、函数等诸多知识密切相关。根据问题条件中的数量关系和结构特征,构造出一个新的方程,然后根据方程的理论,往往能使问题在新的关系下得以转化而获解。遇到等量性问题都可以使用方程,对于一些计算问题也可以运用方程思想来解决,倘若不能或难于直接求的就设法导出它满足的方程,这样,问题就归结为求方程的解了。
【例1】已知2 f(x)+f(-x)=3x+2,求函数f(x)的解析式。
分析:将“f(x)”和“f(-x)”看作两个未知数,因此还需要构造一个关于“f(x)”和“f(-x)”的方程,用解方程组的方法来解。
解:将方程组中的“x”用“-x”替换,
则有2f(-x)+f(x)=-3x+2
因此可得方程组
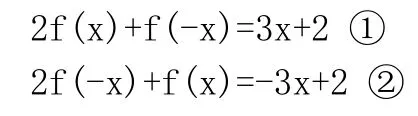
消去“f(-x)”,可得f(x)=3x+
点评:本题考查了用方程思想解函数方程问题,关键在于构造一个同类方程,用消元方法解决。
2.构造数列法
对于数列中一些非等差、非等比问题,特别是数列相邻两项是线性关系的题型,可以灵活的利用题目中的条件,巧妙地构造一个等差或等比数列,使问题转化为我们熟悉的基本问题来解决。
【例2】若求数列{an}的通项公式。
分析:题设条件是一个递推关系,数列{an}既不是等差数列,也不是等比数列,若想通过常规的公式法求通项公式不可能达到目的。经观察分析题设条件,属于an+1=pan+q(p、q是常数)型,用待定系数法求解,即令an+1+A=p(an+A),(A为常数),与原式比较,求得A后,构造等比数列,进而达到求{an}通项公式的目的。
解:设则an+1
令得A=-3.
即变为
∴{an-3}是首项为an-3=-2,公比为的等比数列。
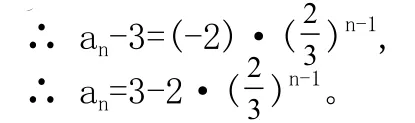
即的通项公式:
点评:本题是求数列通项公式的典型题目,方法是构造等比数列求解,将问题转化后,先利用公式法求出等比数列{an-3}的通项公式,进而求出数列{an}的通项an。
3.构造函数(或图像)法
在直接求解某些数学问题有困难时,我们往往根据问题的条件,构想组合一种新的函数关系,使问题在新的观念下转化,并利用函数的有关性质,借助数形结合方法解决问题,是一种行之有效的解题手段。
【例3】若关于x的方程有负实数根,求实数a的取值范围。
分析:本方程中未知数x处在指数上,如果用代数的方法,则通过有负实数解而要求实数a的取值范围较难入手。如果换一种思维方法,构造指数函数和常数函数,对问题进行转化,用数形结合的方法求解,则问题变得简捷。
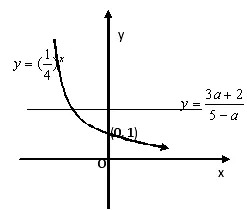
解:令为常数函数。方程有负根,反映在函数图象上就是两函数曲线有交点且交点在y轴左侧(如图),故只须即可,于是由
∴ 实数a的取值范围为:<a<5}
点评:方程与函数是密切联系着的两个数学概念,方程的解是相应函数图象交点的横坐标,因此对一些解起来很困难的方程,用数形结合的方法求解是很重要的方法,本题通过构造指数函数,常数函数,用数形结合的方法,以形助数达到简捷解题的目的。
构造法有利于提高转化化归思想的深刻性,从上述四个例子的解题实践中,我们看到构造法在中学数学解题中所发挥出的化难为易的强大威力,要求教师在长期的教学过程中潜移默化的让学生掌握。
