基于过分割的多目标阈值图像分割算法

赵 凤, 惠房臣, 韩文超

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

基于过分割的多目标阈值图像分割算法

赵 凤, 惠房臣, 韩文超

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

提出一种基于过分割的多目标阈值图像分割算法。使用分水岭算法获得待分割图像的过分割区域和分割边界，将类间方差函数和熵函数作为优化目标函数，采用多目标阈值算法对区域的代表点及分割边界上的像素进行划分，再将区域代表点的划分结果扩展到各区域中，以获得整幅图像的分割结果。在多幅Berkeley图像上进行分割测试，并以分割准确率作为算法性能的评价指标，结果显示，新方法在大多数情况下能够获得高于最大类间方差法和最大熵法的分割准确率，此外，由于图像区域信息的使用，使得图像目标能够较为完整地从背景中分离出来。

多目标优化；阈值分割；类间方差；熵；过分割

在图像分割的诸多方法中，阈值化技术[1-4]是一类简单有效的方法，其中，最大类间方差法[2]和最大熵法[3]是两个最常用的分割算法。

最大类间方差法原理简单，容易实现，对于大多数图像都能得到较好的分割效果。然而，当图像中目标与背景的面积相差很大，或者图像直方图中没有明显的双峰时，最大类间方差法的分割效果不佳。最大熵法在图像的总体轮廓和边界细节保持方面比较好，但当目标和背景的区别不是很明显时，该方法无法获得理想的分割效果。最大类间方差法和最大熵法的上述缺点是因为没有利用图像的区域信息造成的。

不同的阈值准则具有不同的特性，可以在多个阈值准则下寻求均衡，采用多目标优化来解决图像分割问题。多目标优化算法是函数优化领域的一个研究热点[5-8]，它在多个目标间协调权衡，使得所有目标函数尽可能达到最优。

针对阈值分割方法未考虑图像区域信息及准则单一的问题，本文拟给出一种基于过分割的多目标阈值图像分割(Multi-objective thresholding image segmentation based on over-segmentation，MOTIS_OS)算法，即引入分水岭算法[9]，获得图像的过分割区域和分割边界，以保证分割结果中保留图像中的区域信息和边缘信息，并采用多目标优化算法[8]在类间方差和熵两个阈值准则下，对获得的过分割区域代表点和分割边界上的像素进行划分，进而将区域代表点的划分结果扩展到各区域中，获得整幅图像的分割结果。

1 基于过分割的多目标阈值分割

1.1 分水岭过分割

分水岭算法是一种基于数学形态学的分割方法[9-11]。该算法简单、速度快，且对图像的微弱边缘比较敏感。MOTIS_OS算法采用分水岭算法对图像进行过分割，将每个分割区域的灰度均值作为区域代表点，将所有区域的代表点和位于分水岭上的像素灰度作为后续处理的数据集。分水岭过分割的目的是为了保留图像的区域信息和边缘信息。

1.2 多目标阈值分割

为了兼顾类间方差和熵阈值准则的优良特性[2-3]，采用第二代非支配排序遗传算法(Non-dominated sorting genetic algorithm II，NSGA-II)[8]同时优化这两个阈值准则，实现分水岭过分割获得的区域代表点及分割边界上像素的划分。

在多目标优化问题中，很难找到一个解使得所有目标函数同时最优，因此多目标优化最终所得的是一个折衷解的集合，称为Pareto最优解集(或非支配解集)。对于两个解x1和x2，称为x1Pareto支配x2，当且仅当对所有子目标，x1不比x2差，且至少存在一个子目标，使得x1比x2好。一个解x*被称为Pareto最优解(或非支配解)，当且仅当不存在其他解xPareto支配x*。所有Pareto最优解构成的集合称为Pareto最优解集。

多目标阈值分割算法的基本要素包括染色体编码、种群初始化、适应度函数设计、非支配排序与拥挤距离计算、选择、交叉与变异操作、精英策略和最优解的选择。

(1) 染色体编码与种群初始化

染色体表示问题的可能潜在解。MOTIS_OS算法对灰度阈值进行编码，编码方式采用实数制编码，编码范围是0～255。

初始种群中每个染色体按照如下方式产生：随机产生一个0到1之间的随机数d，则该染色体为[255d]。设定种群大小为80，最大代数G=100。

(2) 适应度函数

适应度函数用来描述种群中染色体的性能。MOTIS_OS算法采用类间方差函数和熵函数作为多目标优化的两个适应度函数。

设N表示一幅图像中包含的像素数目，[0,L]表示图像灰度级范围，ni表示灰度级为i的像素个数，则灰度级i的出现概率

假设t表示选取的图像阈值，类间方差函数主要考察该阈值下获得的图像目标和背景这两个类之间的方差，定义为

f1(t)=W0(u0-uT)2+W1(u1-uT)2,

其中

分别表示图像背景和目标出现的概率，而

分别表示图像背景的灰度均值、图像目标的灰度均值和整幅图像的灰度均值。

通常利用类间方差f1(t)的最大化来获取最佳的阈值t*。

假设t表示选取的图像阈值，熵函数主要考察该阈值下获得的图像目标和背景的熵之和，定义为

f2(t)=H0(t)+H1(t),

其中

分别为图像背景的熵和目标的熵。

某一阈值t对应的熵函数f2(t)越大，则认为分割结果保留原图像中的信息越多，则该阈值t越优。

(3) 非支配排序与拥挤距离计算

非支配排序[8]是将种群按支配关系分成若干层，第一层为当代种群中非支配个体的集合，该集合中所有个体的序值均为1；第二层是种群去掉第一层个体后非支配个体的集合，该集合中所有个体的序值均为2，以此类推，将种群中所有个体排序。

拥挤距离[8]用于比较非支配排序后同级中不同个体的性能。某个个体的拥挤距离是通过计算与该个体相邻的两个个体的每个目标函数的距离之和获得的。

(4) 选择、交叉与变异操作

选择就是挑选染色体产生交配池的过程，为交叉和变异操作准备父代染色体。MOTIS_OS算法采用拥挤二进制锦标赛选择方法[8]产生交配池，即采用锦标赛办法，按照个体的非支配排序等级和拥挤距离从初始种群中选择出一半数量的个体作为父代。

交叉操作是按照一定的交叉概率对两个染色体进行交配重组，产生新的染色体。设置交叉概率为0.9，交叉操作采用模拟二进制交叉方法[12]，其中，交叉分布指数设置为20。

变异操作是按照一定的变异概率对染色体的基因位进行修改，可在种群中引入缺失的基因，以实现对可行解空间的全局搜索。设置变异概率为0.1，变异操作采用多项式变异[13]，其中，变异分布指数设置为20。

(5) 精英策略和最优解的选择

采用NSGA-II算法作为多目标框架来解决阈值分割问题。众所周知，NSGA-II算法最具特色的部分就是它的精英操作。通过精英操作，父代和子代中的非支配解会遗传到下一代种群中，因此，迄今为止发现的最优解就会被保留下来。

算法最终获得的是由非支配解构成的一个集合。在理论上，所有非支配解都同等重要，然而，在实际应用中，用户往往只需要一个解。根据多次实验发现，非支配解集中的前两个解对应的视觉分割效果较好，故可从中选择一个作为最终解。

按照最优解(即最优阈值)对区域代表点及分水岭边界上的像素进行划分，并将区域代表点的划分结果扩展到各区域中，从而获得整幅图像的分割结果。

1.3 算法流程

MOTIS_OS算法的具体流程如图1所示。

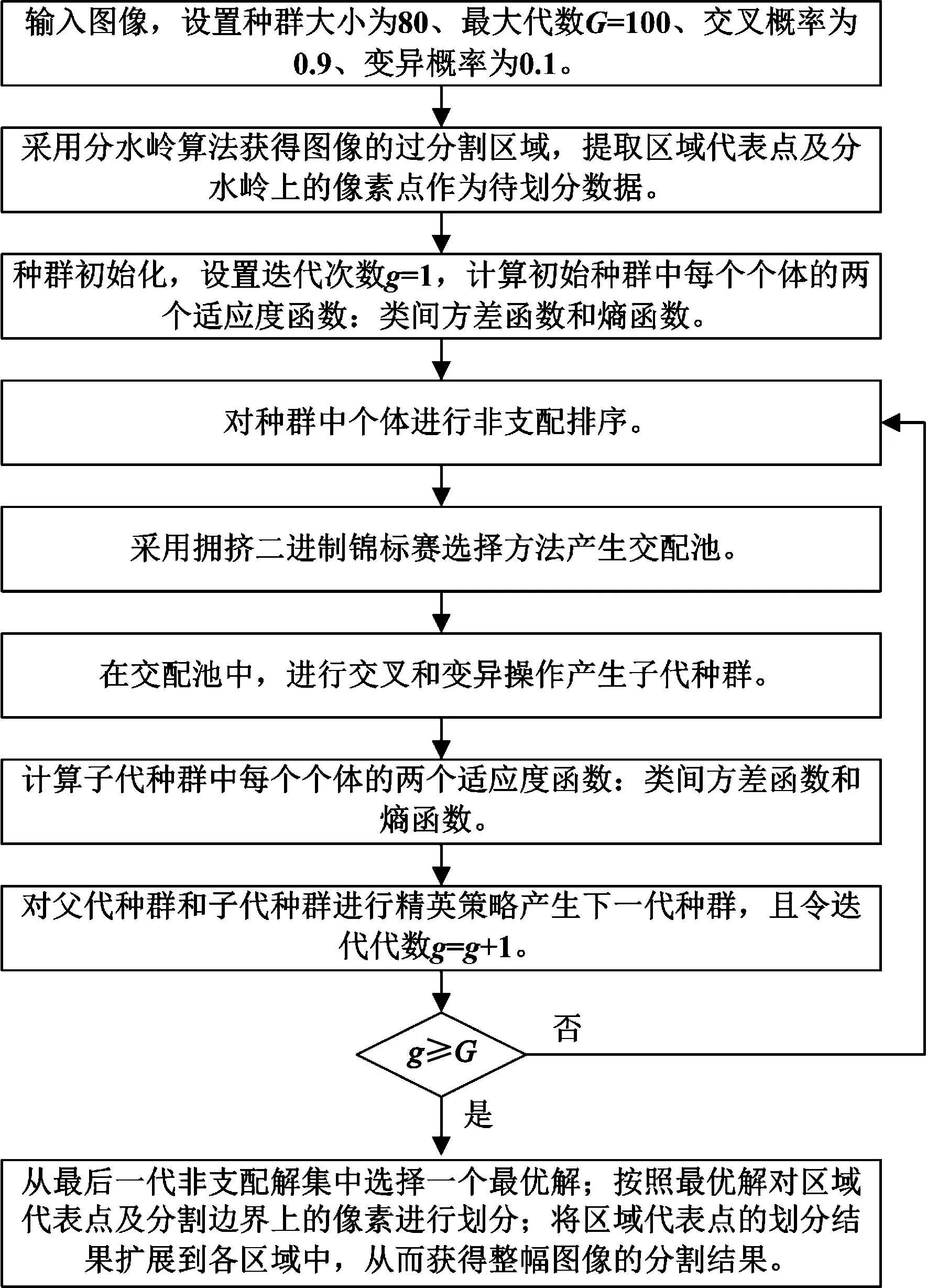
图1 MOTIS_OS算法流程

2 实验结果与分析

实验中采用最大类间方差法和最大熵法作为比较算法。采用5幅Berkeley图像[14]作为实验图像，如图2所示。5幅图像的分割结果分别如图3至图7所示，其中，每幅图像的标准分割结果在(a)图中给出，最大类间方差法的分割结果在(b)图中给出，最大熵法的分割结果在(c)图中给出，MOTIS_OS算法的分割结果在(d)图中给出。

如图3所示，对于图像#3096，虽然三种算法都将部分背景错分成了目标，但MOTIS_OS算法的错分区域最小，而且飞机机身保持的最好，其分割结果最接近标准分割结果。

对于图像#42049，最大类间方差法和最大熵法都存在把位于图像四角处的背景错分为目标的现象，MOTIS_OS算法的分割结果大大改善了这一问题，但在树枝末端存在细节信息丢失的现象，具体结果可参见图4。

(a) 图像#3096(b) 图像#42049(c) 图像#135069 (d) 图像#3063(e) 图像#8068

图2 实验图像

如图5所示，最大熵法将图像#135069的大部分目标错分为背景，只分割出了小部分目标，最大类间方差法和MOTIS_OS算法的分割结果比较理想，MOTIS_OS算法在细节信息保持上要优于最大类间方差法，具体见图5(c)和图5(d)。

如图6所示，最大类间方差法错将图像#3063的背景分为目标飞机，最大熵法和MOTIS_OS算法的分割结果比较令人满意，但最大熵法背景处还存在一些错分点，MOTIS_OS算法在飞机螺旋桨处有少量信息丢失的问题，具体见图6(c)和图6(d)。

从图7可以看出，由于图像#8086中水中倒影的存在，使得三种算法的分割结果均不是很理想，最大熵法受水中倒影的影响最大，最大类间方差法存在部分目标信息丢失的问题，MOTIS_OS算法获得了相对较好的分割结果，具体见图7(d)。

(a) 标准分割 (b) 最大类间方差法

(c) 最大熵法 (d) MOTIS_OS算法

图3 图像#3096分割结果

(a) 标准分割 (b) 最大类间方差法

(c) 最大熵法 (d) MOTIS_OS算法

图4 图像#42049分割结果

(a) 标准分割 (b) 最大类间方差法

(c) 最大熵法 (d) MOTIS_OS算法

图5 图像#135069分割结果

(a) 标准分割 (b) 最大类间方差法

(c) 最大熵法 (d) MOTIS_OS算法

图6 图像#3063分割结果

(a) 标准分割 (b) 最大类间方差法

(c) 最大熵法 (d) MOTIS_OS算法

图7 图像#8068分割结果

综合以上分割结果可以发现，由于MOTIS_OS算法利用了图像的区域信息，使得目标能够较为完整的从背景中提取出来，在大多数情况下获得了优于最大类间方差法和最大熵法的视觉分割效果。

每幅Berkeley图像都有标准分割结果，故可采用分割准确率[15]来定量评价各个算法的性能。各个算法在5幅Berkeley图像上获得的分割准确率如表1所示。

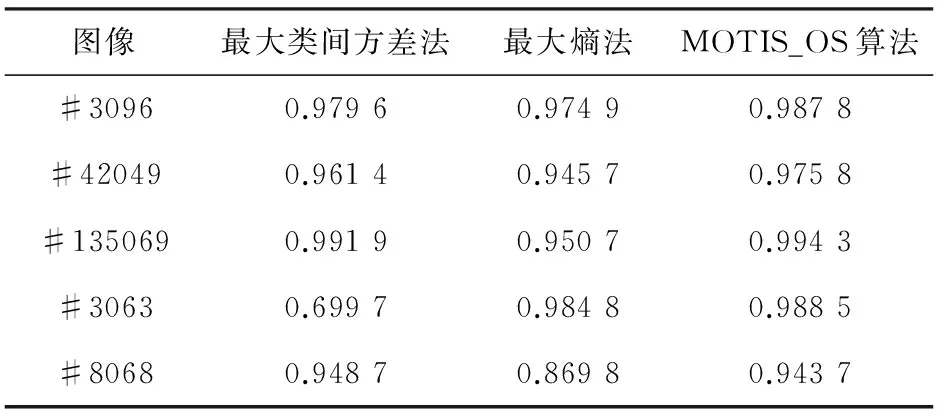
表1 各算法分割准确率对比

由表1可知，MOTIS_OS算法在图像#3096、图像#42049、图像#135069和图像#3063上的分割准确率都是三种算法中最高的；对于图像#8068，MOTIS_OS算法的分割准确率略低于最大类间方差法。表1中数据统计与前面的视觉评价结果基本一致，表明MOTIS_OS算法的分割性能是比较理想的，能够在大多数情况下获得优于最大类间方差法和最大熵法的分割结果。

3 结语

提出了一种基于过分割的多目标阈值图像分割算法，由于图像区域信息的使用，使得图像目标能够较为完整地从背景中分离出来。在多幅Berkeley图像上进行了验证，实验结果表明，该算法在大多数情况下能够获得高于最大类间方差法和最大熵法的分割准确率。

该算法的最优解是从最后一代非支配解集中按照视觉分割效果选择的，因此，最优解的自适应选择仍是一个值得研究的问题。此外，该算法仅适用于单阈值分割，如何将算法扩展到多阈值分割也值进一步研究。

[1] 谢勰, 王辉, 张雪锋. 图像阈值分割技术中的部分和算法综述[J]. 西安邮电学院学报, 2011, 16(3): 1-5.

[2] Otsu N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1979, 9(1): 62-66.

[3] Kapur J N, Sahoo P K, Wong A K C. A new method for gray-level picture thresholding using the entropy of the histogram[J]. Computer Vision, Graphics and Image Processing, 1985, 29(3): 273-285.

[4] 赵凤, 范九伦. 融合灰度和非局部空间灰度特征的二维Otsu法[J]. 西安邮电学院学报,2012,17(3): 10-14.

[5] 郑金华. 多目标进化算法及应用[M]. 北京: 科学出版社, 2010: 21-26.

[6] 公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2): 271-289.

[7] 张蕾蕾. 半局部凸多目标半无限规划的对偶性[J]. 西安邮电学院学报, 2008, 13(5): 145-147.

[8] Deb K, Agrawal S, Pratab A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II[C]//Proceedings of the Parallel Problem Solving from Nature VI Conference. France Paris: Springer, 2000: 849-858.

[9] Vincent L, Soille P. Watersheds in digital space: an efficient algorithm based on immersion simulation[J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 1991, 13(6): 583-598.

[10] 余旺盛, 侯志强, 宋建军. 基于标记分水岭和区域合并的彩色图像分割[J]. 电子学报, 2011, 39(5): 1007-1012.

[11] Yang H G, Ahuja N. Automatic segmentation of granular objects in images: combining local density clustering and gradient-barrier watershed[J]. Pattern Recognition, 2014, 47(6): 2266-2279.

[12] Beyer H G, Deb K. On self-adaptive features in real-parameter evolutionary algorithm[J]. IEEE Transactions on Evolutionary Computation, 2001, 5(3): 250-270.

[13] Raghuwanshi M M, Kakde O G. Survey on multiobjective evolutionary and real coded genetic algorithms[C]//Proceedings of the 8th Asia Pacific Symposium on Intelligent and Evolutionary Systems. Australia Cairns: Springer, 2004: 150-161.

[14] Martin D, Fowlkes C, Tal D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]//Proceedings of Eighth IEEE International Conference on Computer Vision. Canada Vancouver: IEEE, 2001: 416-423.

[15] Wu M, Schölkopf B. A local learning approach for clustering[C]//Advances in Neural Information Processing Systems. American Cambridge: MIT, 2007: 1529-1536.

[责任编辑:瑞金]

Multi-objective thresholding image segmentation algorithm based on over-segmentation

ZHAO Feng, HUI Fangchen, HAN Wenchao

(School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A multi-objective thresholding image segmentation algorithm is presented in this paper based on over-segmentation. The watershed algorithm is firstly used to obtain the over-segmentation regions and boundaries of an image; then the multi-objective thresholding algorithm, which adopts the variance between clusters and the entropy as the objective functions, is used to partition the representative points of the segmentation regions and the pixels on the boundaries; finally the partitioning results of the representative points are extended to their respective segmentation regions to acquire the segmentation result of the whole image. Some Berkeley images are adopted in the segmentation experiment and the segmentation accuracy is used as the evaluation index of algorithm performance. Experimental results show that the new method can obtain higher segmentation accuracy than the maximum variance between clusters method and the maximum entropy method in most cases. Moreover, the object can be more completely partitioned from the background due to utilizing the image region information.

multi-objective optimization, thresholding segmentation, variance between clusters, entropy, over-segmentation

2015-02-05

国家自然科学基金资助项目(61102095, 61202153);陕西省科技计划资助项目(2014KJXX-72); 陕西省自然科学基础研究计划资助项目(2012JQ8045, 2014JQ8336); 中央高校基本科研业务费专项基金资助项目(GK201503063)

赵凤(1980-)，女，博士，副教授，从事模式识别、图像处理和模糊信息处理研究。E-mail: fzhao.xupt@gmail.com 惠房臣(1991-)，男，硕士研究生，研究方向为信号与信息处理。E-mail: 390620477@qq.com

10.13682/j.issn.2095-6533.2015.03.010

TP751

A

2095-6533(2015)03-0060-05