基于核主成分分析的三维模型分类算法

王鹏飞，舒振宇，于欣

(1.太原科技大学电子信息工程学院，太原 030024;

2.浙江大学宁波理工学院信息科学与工程学院，浙江 宁波 315100)

基于核主成分分析的三维模型分类算法

王鹏飞1，舒振宇2，于欣2

(1.太原科技大学电子信息工程学院，太原 030024;

2.浙江大学宁波理工学院信息科学与工程学院，浙江 宁波 315100)

针对三维模型的分类问题，提出了一种基于核主成分分析(Kernel-Principal Components A-nalysis，K-PCA)的三维模型分类算法。该算法首先选择形状直径函数(Shape Diameter Function，SDF)作为特征描述符来提取三维模型的特征向量;然后使用核函数将原始特征向量映射到高维空间中并在该空间上进行PCA得到新的特征向量;最后使用KNN算法并计算未知模型与已知类别的k个模型之间的l2范数以实现模型的分类，确定未知模型的类别。实验结果表明，该算法能够很好的识别三维模型的几何特征，能准确的区分不同类别的三维模型，具有较高的分类准确率。

核主成分分析;三维模型;K近邻;分类;形状直径函数

继数字声音、数字图像和数字视频之后，第四代多媒体数据类型——数字几何模型已经成为数字媒体技术的新发展趋势。而作为数字几何研究主体之一的三维模型正被广泛应用于工业设计、影视动画和分子生物学等领域。三维模型是指对真实物体的表面进行采样、处理而得到的多边形几何数据。随着大量三维模型的出现，对三维模型的相关研究工作也越来越多，其中三维模型分类就是一个重要问题。

三维模型分类(3D Model Classification)指的是如何根据离散曲面的内在几何特征和内在语义特征，来对未知模型与已知类别的模型之间进行相似性度量，从而判断未知模型的类别。三维模型分类算法对于基于内容的模型检索具有重要的意义，目前国际上大部分三维模型数据库在检索方面提供的方法仍然是基于人工文本标签的方式，即通过人工的方式，为模型库中每个模型加上若干个文本标签，用来描述对应的模型。然后再由用户通过搜索这些文本标签来定位到相应的网格模型。该方法需要的人工量巨大，因此，急需某种算法能够自动从曲面本身内在特征的角度来进行模型的检索和分类。三维模型分类的关键在于如何选取特征描述符(Feature Descriptor)，该描述符是模型内在特征的抽象描述，一般要求其与模型的旋转、平移、缩放无关。基于特征描述符，模型之间相似程度的衡量可以转化为对其相应特征描述符的比对。目前，网格模型分类算法［1-7］主要包括基于全局几何特征的方法，基于局部几何特征的方法，以及基于图像特征的方法。如刘斌等［8］将PCA与ICP算法相结合，利用PCA方法将模型进行初始定位，并用ICP进行校准，最后利用差值平方和函数对模型的相似性进行度量。Wang等［9］使用核密度来估计样本特征空间的分布进而对三维模型进行分类。冯立颖等［10］将三维模型轮廓上角点的曲率作为模型特征来提取，并使用Hausdorff距离进行相似性比较。陈俊英等［11］将多个RBF神经网络进行了集成，得到三维模型的特征信息，进而对模型进行分类。高思明等［12］提出了一种基于谱特征和深度信任网络的模型分类方法。首先通过深度信任网络对模型的谱特征进行降维，再使用支持向量机对模型进行分类。付小君等［13］提出一种基于统计特征量和Markov模型的分类算法，首先对三维模型进行切分并将各分块的统计特征量作为Markov模型的伪时间序列，进而对模型进行分类。一些非线性流形学习的方法［14-15］也被应用到了三维网格模型分类问题上，并取得了一定的效果。

本文提出了一种基于核主成分分析(Kernel-Principal Components Analysis，K-PCA)的三维模型分类算法。针对三维模型姿势不同对分类效果的影响，本文将具有姿势不变的形状直径函数(Shape Diameter Function，SDF)作为特征描述符，提取出表现三维模型形状特征的特征向量。在选择特征向量的维数时会出现:若维数选择过低，特征向量所包含的模型特征信息会很少;若维数选择过高，虽然特征向量包含大量特征信息，但由于维数过高在计算时会出现“维数灾难”问题。这都会影响模型分类的效果。为解决以上问题，本文采用核函数将原始特征向量进行非线性高维映射并在高维空间中使用PCA以得到新的特征向量。算法的具体流程如图1所示。

1 选择特征描述符

三维模型是由三维空间中的三角面片通过边和顶点的连接而形成的分片线性曲面，其中每条边最多只能包含在两个三角面片中。对于三维模型，可以用M={V}来表示，其中V={Ωi}(i=1，2，，p)，p为三维模型表面顶点的个数，每个顶点Ωi包含空间坐标值(xi，yi，zi).为将三维模型的形状特征用数值表现出来，就需要选择特征描述符对三维模型进行特征提取。本文使用形状直径函数(SDF)作为三维模型的特征描述符，提取出表现三维模型形状特征的特征向量。

形状直径函数(SDF)最初被应用在模型分割和骨架提取方面，这一概念是由Shapira［16］等提出的。三维模型可以看作是由多个二维网格表面围成具有一定体积的特定空间，SDF就是定义在这些网格表面的标量函数，它将三维模型的体积信息映射到其包围的二维网格表面上，以实现对三维模型形状特征的数值描述。使用SDF提取三维模型特征向量的具体步骤如下:

(1)计算三维模型表面三角面片中心点的SDF值

给定三维模型表面三角面片中心的一点ϑi(i= 1，2，，s)，其中s为三维模型表面三角面片的个数，在该点法线→n的反方向做一圆锥体，圆锥角的角度一般可选为120°.在圆锥体的内部从点ϑi向模型内部做射线段，均匀选择若干条射线(一般情况下可选30条)并计算这些射线段的长度，将这些射线段长度的加权平均值作为该点的SDFi值。

(2)提取三维模型的特征向量

给定任意三维模型Mi，j(i=1，2，，n;j=1，2，，m)，其中n为三维模型的类别数，m为每类模型的个数。计算三维模型表面三角面片中心点ϑi(i= 1，2，，s)处的形状直径函数值SDFi和该三角面片的面积fi(i=1，2，，s)，其中s为三维模型表面三角面片的个数，将所有的SDFi(i=1，2，，s)值进行加权直方图统计，其中权值为fi(i=1，2，，s)，将区间［min(SDFi)，max(SDFi)］平均分成L个子区间，L即为模型特征向量的维数。将位于第j(j= 1，2，，L)个子区间内所有SDF值所对应的权值fi进行加和，得到每个子区间的权重qj(j=1，2，，L)，最后对L个qj做归一化处理即可得到模型的特征向量wi，j∈RL×1(i=1，2，，n;j=1，2，，m).

2 K-PCA算法描述

主成分分析(Principal Component Analysis，PCA)是对数据进行特征提取的重要手段。每一个主成分都是数据在某一个方向上的投影，在不同的方向上这些数据方差的大小由其对应的特征值决定。一般会选取较大的几个特征值所对应的特征向量，这些方向上的信息丰富，包含更多重要特征信息。PCA算法已经应用在二维图像的识别中并取得较好的识别效果，如张秀琴等［17］将DCT和改进的2D2PCA算法相结合，从而克服了二维主成分分析在鲁棒性、识别速率上的不足，并成功应用人脸识别中。但PCA的内部模型是线性的，这就大大限制了PCA的应用范围。对于所研究对象是非线性的情况下，就需要利用核函数对PCA进行非线性推广。K-PCA算法首先利用一个非线性映射函数Φ将数据从输入空间X映射到高维空间F中，然后对映射数据在空间F中实现PCA.K-PCA是一种非线性方法，它能有效的提取非线性特征。

2.1 算法原理

设x，z∈X，X属于R(n)空间，非线性函数Φ实现输入空间X到高维空间F的映射，其中F属于R(m)，n＜＜m.根据核函数技术有:

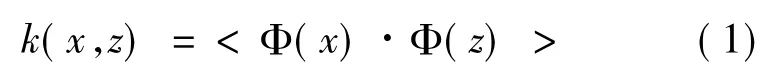
其中:＜·＞为内积，K(x，z)为核函数。由式(1)可知，核函数将m维高维空间的内积运算转化为n维低维输入空间的核函数计算，从而有效地解决了在高维特征空间中确定非线性映射函数的形式和参数、特征空间维数和计算时的“维数灾难”等问题。

PCA的算法原理为:假设有n个样本X=［x1，x2，，xn］∈Rl×n，PCA的目的就是找到一系列的特征向量，使得样本数据在这些特征向量上的投影方差尽量大。计算样本的均值为并对样本数据进行预处理di=xi-u(i=1，2，，n)，使得新样本数据的协方差矩阵为C=Rl×n.求协方差矩阵C的特征值λ和特征向量v，即Cv=λv.选择特征值λ1≥λ2≥≥λn的前q个较大特征值对应的特征向量V=［v1，v2，，vq］作为样本的q个投影方向，得到PCA处理之后的样本数据X'=［x1，x2，，xn］∈Rq×n，其中q≤l.

K-PCA是使用核函数对PCA的非线性推广，将样本数据X=［x1，x2，，xn］∈Rl×n通过非线性函数Φ映射到高维空间F中，即xi→Φ(xi)(i=1，2，，n).首先要对样本数据进行预处理，得到di=xiu(i=1，2，，n)，然后使用非线性函数Φ对数据进行高维映射di→Φ(di)，计算经过核函数映射的样本数据的协方差矩阵其中DΦ=［Φ(d1)，Φ(d2)，，Φ(dn)］T.令K=DΦ(DΦ)T，则有:

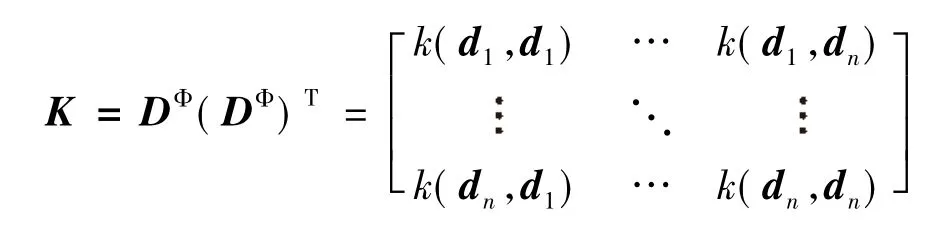
由于非线性函数Φ的参数和形式未知，因而无法直接求取协方差矩阵CΦ的特征值与特征向量。所以需要先求解KuΦK=λΦKuΦK，其中K已知，λΦK和uΦK分别为矩阵K的特征值和特征向量。通过:

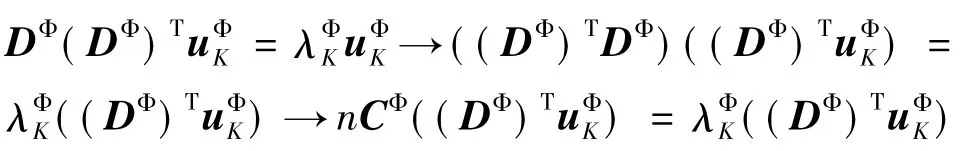
转化即可求CΦvΦ=λΦCvΦ，得到协方差矩阵CΦ的特征值λΦC与特征向量vΦ，在高维空间F中，样本数据［Φ(d1)，Φ(d2)，，Φ(dn)］在特征向量vΦ上的投影为:

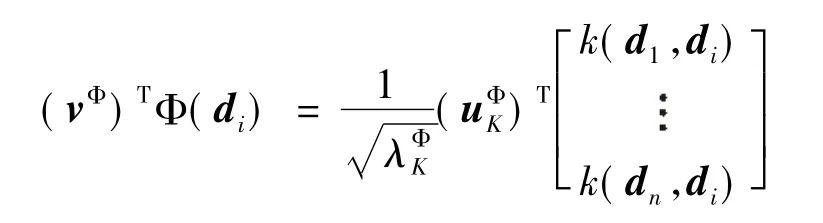
其中(i=1，2，，n)，选择前q个较大特征值对应的特征向量VΦ=［vΦ1，vΦ2，，vΦq］，将样本数据Φ(di)在这q个方向上做投影，得到在高维空间F上的PCA，即XΦ=［xΦ1，xΦ2，，xΦn］∈Rq×n，其中q≤l.

2.2 本文算法

本文首先利用基于姿势不变的形状直径函数(SDF)来对三维模型进行特征提取，提取出表现其形状特征的特征向量，再利用核函数对特征向量进行高维映射，以克服特征向量的非线性特征对模型分类效果的影响。然后使用主成分分析(PCA)在高维空间中进行降维，提取出三维模型的主要特征。最后使用KNN算法对三维模型进行分类识别。

算法的详细步骤如下:

Step 1:计算三维模型表面三角面片中心点ϑi的形状直径函数值SDFi，其中(i=1，2，，s)，并进行加权直方图统计得到模型的特征向量wi，j∈RL×1，其中(i=1，2，，n;j=1，2，，m)，并对特征特征向量处理得到di，j∈RL×1(i=1，2，，n;j=1，2，，m);

Step 2:将所有三维模型的特征向量组成特征向量矩阵W，选择合适的核函数对其进行高维映射di，j→Φ(di，j);

Step 3:对映射后的矩阵求其协方差矩阵CΦ的特征值和特征向量，然后选择协方差矩阵的前q个较大特征值所对应的特征向量VΦ=［vΦ1，vΦ2，，vΦq］作为PCA的q个主方向;

Step 4:将特征向量Φ(di，j)和未知模型的特征向量yΦ在这q个方向上做投影，得到在高维空间F上的PCA，即WΦ=［WΦ1，WΦ2，，WΦn］∈Rq×mn和yΦ∈Rq.

Step 5:使用KNN算法在WΦ中找到距离yΦ∈Rq最近的k个特征向量A=［wΦ1，wΦ2，，wΦk］∈Rq×k，并计算yΦ∈Rq和A之间的l2范数以实现模型之间的分类，得到未知模型的类别。

3 实验结论与讨论

本文算法在SHREC'11三维模型数据库［18］上进行，该数据库中共有600个非刚体三维模型，根据内容分成30类，每类20个模型。该模型数据库中的部分三维模型如表1所示。

表1 SHREC'11 non-rigid shapes三维模型数据库中的部分模型Tab.1 Parts of the 3D models in SHREC'11 non-rigid shapes database

本实验利用SHREC'11数据库中的三维模型在MATLAB中进行仿真实验。实验采用的计算硬件配置为Inter core(TM)i3 2.4 GHZ CPU，4 G内存。为测试本文算法分类的准确率，本文在模型数据库的每类模型中随机选择10个作为测试模型，剩下的模型作为训练模型，因此测试模型和训练模型各有300个。在300个测试模型中任意选择一个模型，在训练模型中进行分类。用测试模型分类的平均准确率作为算法精确度的评判标准。

3.1 仅使用KNN算法进行模型分类

在使用特征描述符SDF对三维模型提取特征向量并进行直方图统计时，需要考虑特征向量的维数问题，即参数L的取值问题。对原始特征向量不做任何处理只使用KNN算法对模型进行分类，来验证参数L对分类效果的影响，其中参数L取值为25、50、100、200、400.参数L不同取值时模型分类的平均准确率如图2所示。

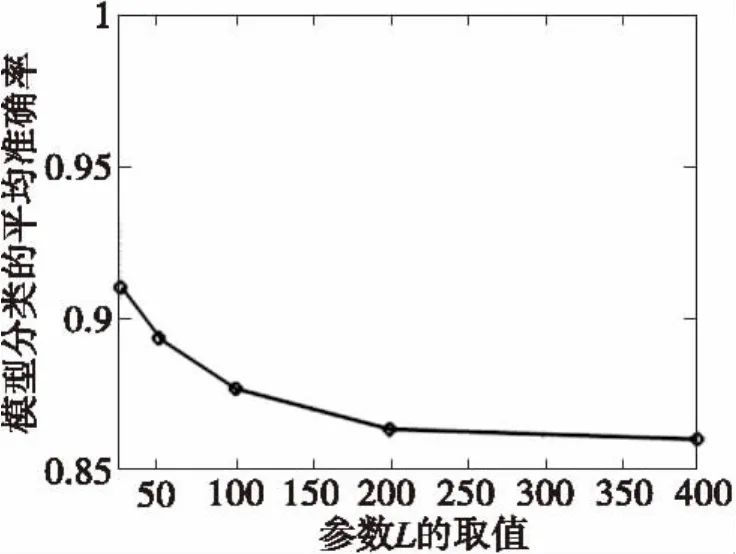
图2 参数L取值不同时的平均准确率(原始特征向量)Fig.2 The average success rates for the different values of the parameter L(the original feature vectors)

由图2可知，随着参数L的增加模型分类的平均准确率总体呈下降的趋势，当L=25时，模型分类的平均准确率为91%，L=400时模型分类的平均准确率下降到86%.显然，参数L选择过大时，虽然特征向量所包含模型的特征信息很多，但是由于“维数灾难”问题，模型的分类效果并不理想。因此需要对原始特征向量进行PCA降维，提取出模型主要的特征信息，以减少由于维数选择对模型分类效果的影响。

3.2 仅使用PCA算法对原始特征向量进行数据降维

对原始特征向量进行主成分分析(PCA)，参数q取5，10，20，30，40，50.即将原始特征向量的维数降为q维，实验结果如图3所示。

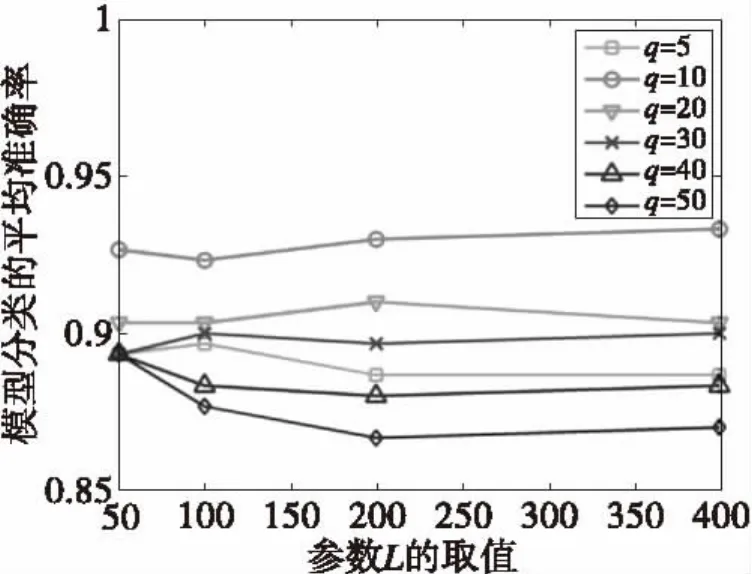
图3 仅使用于PCA算法时不同q值的结果比较图Fig.3 The comparison chart of the result for the different value of q when used in the PCA algorithm

由图3可知，横轴为原始特征向量的维数，纵轴为对原始特征向量经过PCA之后30类模型分类的平均准确率。由图可知，当q=10时，模型的分类效果最好。随着q取值的增加，模型分类的平均准确率逐渐降低。当q=5时，由于经过PCA后的特征向量维数仅为5，新特征向量包含的模型特征信息大量减少，导致模型的分类效果并不理想。因此，在使用PCA算法时，参数q的取值为10，以保证模型的分类效果达到最好。

3.3 使用K-PCA算法对原始特征向量进行处理

本文使用线性核函数k(x，xp)=x*xp、多项式核函数k(x，y)=(a(x·y)+b)d和高斯核函数k (x，y)=exp(-‖x-y‖/2σ2)来对原始数据进行高维映射，并比较不同核函数对模型分类效果的影响，其中K-PCA时的参数q值选为10.实验结果如图4所示。

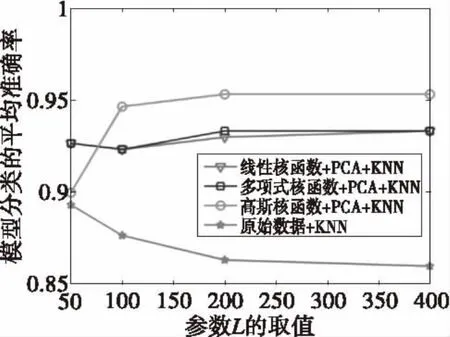
图4 不同核函数比较结果图Fig.4 The comparison results of the different kernel functions

由图4可知，当原始特征向量的维数L=50时，使用K-PCA算法对其进行处理之后，模型分类的准确率比直接使用KNN算法进行分类的效果好。当特征向量维数选择过低造成的特征信息过少时，需要使用核函数对低维数据进行高维映射，再使用PCA算法进行降维，就可以解决由于维数选择过高或过低而对模型分类的影响，从而提高分类的准确度。实验结果表明，由于数据本身是非线性的，单纯使用PCA时的分类效果并不理想。因此使用核函数将原始数据映射到高维空间，在高维空间中对数据进行PCA处理可以得到理想的分类效果。

选定核函数之后，需要比较单纯进行PCA和使用K-PCA这两种情况时的模型分类效果。本文选用高斯核函数，参数q=10.仅使用PCA时，q取值为10.实验结果如图5所示。

由图5可知，如果原始特征向量不经过任何处理就进行模型分类，随着参数L的增加模型分类的准确率逐渐下降。如果原始特征向量只做PCA处理，由于PCA的内部模型是线性的，原始特征向量数据本身是非线性的，因此PCA的效果并不理想。如果将原始数据使用K-PCA进行处理，即使用核函数将原始特征向量映射到高维空间中并在该空间使用PCA提取主要的特征，能够得到好的模型分类效果。如图6所示。

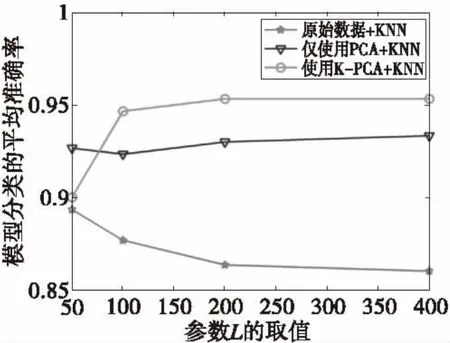
图5 K-PCA与PCA算法的比较结果图Fig.5 The comparison results chart of the PCA and the K-PCA algorithm

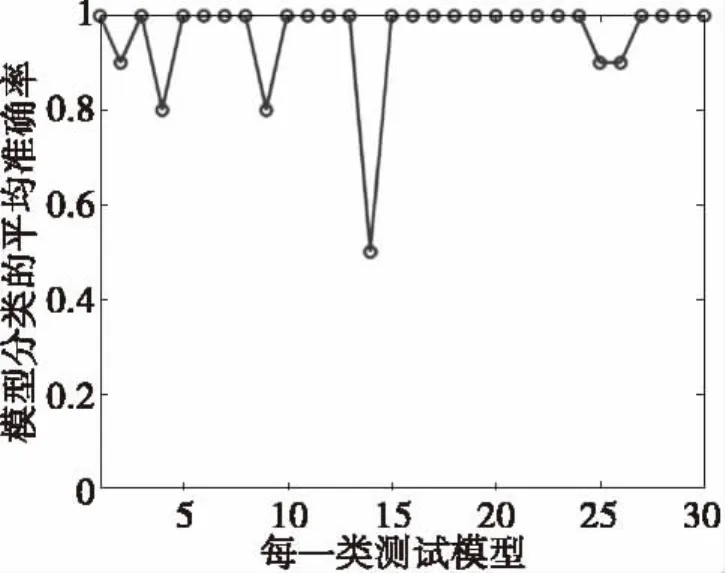
图6 本文算法在各类模型上的平均准确率Fig.6 The average success rates of our algorithm on every kind of model

由图6可知，原始特征向量经过K-PCA算法处理之后，大部分模型分类的准确率都在90%以上，30类模型分类的平均准确率可以达到96%.

本文还对算法在时间和空间的复杂度进行了分析，随着模型种类的增加，算法在时间和空间上的复杂度如图7所示。

由图7可知，当模型数量在100时，耗时为0.174 s，占用的存储空间为0.1 MB.当模型数量增加到600时，耗时增加到0.617 s，占用的存储空间增加到11 MB.

将本文算法与其他多个三维模型识别算法进行比较，如多元支持向量机(multi-support vector machine，MultiSVM)［19］、K近邻以及由Bronstein等［20］提出的SHIKS结合BOF作为特征描述符对三维模型进行分类的新方法等。实验选择SHREC'11数据库中的300个模型作为训练模型，300个模型作为测试模型。表2列出了所用的四种不同算法的分类准确率和所用时间。

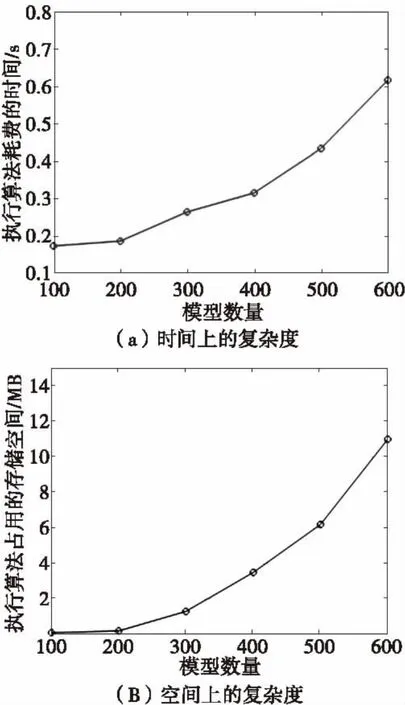
图7 算法在时间和空间上复杂度分析结果图Fig.7 The complexity analysis of the algorithm on the timeand the space

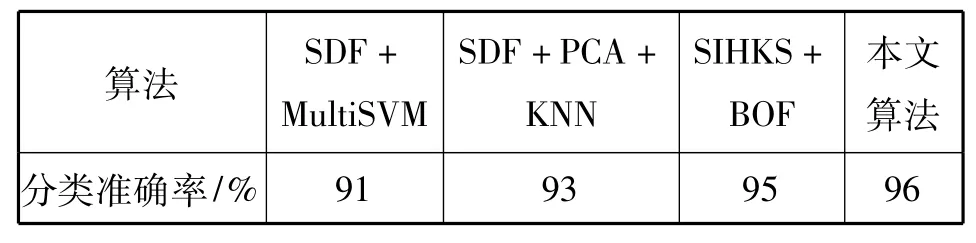
表2 不同算法的分类准确率Tab.2 The average success rates of the different algorithm

实验结果表明，本文算法分类准确率相对较高，所用时间相对较少，更适用于实际应用的三维模型分类识别中。

4 结论

本文提出了一种基于核主成分分析的三维模型分类算法。该算法首先选择形状直径函数(SDF)作为特征描述符提取三维模型的特征向量。在数据本身是非线性的情况下，使用非线性的KPCA算法对三维模型的高维特征向量进行主要特征的提取。最后使用KNN算法对三维模型进行分类。本文算法具有简单、准确率高且易于实现等特点。

［1］ANKERST M，KASTENMüLLER G，KRIEGEL H P，et al.3D shape histograms for similarity search and classification in spatial databases［C］∥Advances in Spatial Databases.Springer Berlin Heidelberg，1999:207-226.

［2］ELAD M，TAL A，AR S.Content based retrieval of VRML objects—an iterative and interactive approach［M］.Springer Vienna，2002，18(3):107-118.

［3］ZHANG C，CHEN T.Efficient feature extraction for 2D/3D objects in mesh representation［C］∥Image Processing，2001.Proceedings of 2001 International Conference on IEEE，2001，3:935-938.

［4］HUBER D，KAPURIA A，DONAMUKKALA R，et al.Parts-based 3d object classification［C］∥Proceedings of the 2004 IEEE Computer Society Conference on IEEE，2004，2:Ⅱ-82-Ⅱ-89.

［5］CHUA C S，JARVIS R.Point signatures:A new representation for 3d object recognition［J］.International Journal of Computer Vision，1997，25(1):63-85.

［6］KAZHDAN M，FUNKHOUSER T，RUSINKIEWICZ S.Rotation invariant spherical harmonic representation of 3 D shape descriptors［C］∥Symposium on geometry processing.2003.

［7］OSADA R，FUNKHOUSER T，CHAZELLE B，et al.Matching 3D models with shape distributions［C］∥Shape Modeling and Applications，SMI 2001 International Conference on IEEE，2001:154-166.

［8］刘斌，上官宁，江开勇.三角网格模型分类分析［J］.华侨大学学报:自然科学版，2009，30(6):606-609.

［9］WANG Y，LU T，GAO R，et al.3D model comparison through kernel density matching［C］∥Pattern Recognition(ICPR)，2010 20th International Conference on IEEE，2010:3159-3162.

［10］冯立颖赵静杨莹.基于轮廓特征点的三维模型相似性分类算法［J］.计算机应用，2010，30(4):914-916.

［11］陈俊英，王羡慧，方亚萍.基于RBF神经网络集成的三维模型分类和检索［J］.图学学报，2013，34(2):26-30.

［12］高恩阳，刘伟军，王天然，等.基于谱特征和深度信任网络的三维模型分类［J］.机械设计与制造，2013(3):250-252.

［13］付小君，郭鹏江，郭竞，等.统计特征和Markov模型在三维模型分类中的应用［J］.Computer Engineering and Applications，2011，47(4):157-159.

［14］ZHU K P，WONG Y S，LU W F，et al.3D CAD model matching from 2D local invariant features［J］.Computers in industry，2010，61(5):432-439.

［15］CHANG J S，SHIH A C C，LIN H Y，et al.3-D mesh representation and retrieval using Isomap manifold［C］∥Multimedia Signal Processing，2008 IEEE 10th Workshop on IEEE，2008:541-546.

［16］SHAPIRA L，SHAMIR A，COHEN-OR D.Consistent mesh partitioning and skeletonisation using the shape diameter function［J］.The Visual Computer，2008，24(4):249-259.

［17］张秀琴，陈立潮，潘理虎，等.基于DCT和分块2D2PCA的人脸识别［J］.太原科技大学学报，2014，35(5):333-338.

［18］Shape Analysis Research Project.SHREC'11 3D Models Dataset［EB/OL］.［2014-10-09］.http:∥www.itl.nist.gov/iad/vug/ sharp/contest/2011/Non.

［19］LIU Y G，YOU Z S，CAO L P.A novel and quick SVM-based multi-class classifier［J］.Pattern Recognition，2006，39(11): 2258-2264.

［20］BRONSTEIN M M，KOKKINOS I.Scale-invariant heat kernel signatures for non-rigid shape recognition［C］∥Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Los Alamitos:IEEE Computer Society Press，2010:1704-1711.

3D Model Classification Algorithm Based on Kernel Principal Component Analysis

WANG Peng-fei1，SHU Zhen-yu2，YU Xin2
(1.College of Electronic and Information Engineering，Taiyuan University of Science and Technology，

Taiyuan 030024，China;2.School of Information Science and Engineering，Ningbo Institute of Technology，Zhejiang University，Zhejiang Ningbo 315100，China)

In order to solve the problem of 3D model classification，a new algorithm，which is based on Kernel Principal Component Analysis(K-PCA)，is proposed.The algorithm firstly selects the Shape Diameter Function(SDF) as the feature descriptor to extract the original feature vectors.Then the original feature vectors are mapped to a high-dimensional space，and the PCA is adopted to reduce the dimension of original data for getting the new feature vectors.Finally，the KNN algorithm is applied to find k models in the known 3D model database，and the l2-norm between the unknown 3D model and the k models is calculated to predict the membership of the unknown model.The experimental results show that the algorithm can identify the geometry features of the 3D models and distinguish the difference of the models precisely.Besides，the algorithm is highly accurate.

Kernel-principal component analysis，3D Models，K-Nearest neighbor，classification，shape diameter function

TP391

A

10.3969/j.issn.1673-2057.2015.02.008

1673-2057(2015)02-0118-08

2014-11-06

国家自然科学基金(11226328，61374096);浙江省自然科学基金(LY13F020018);宁波市自然科学基金(2012A610068)

王鹏飞(1989-)，女，硕士研究生，主要研究方向为计算机图形学;通讯作者:舒振宇，副教授，E-mail:shuzhenyu@ 163.com