基于MIMIC算法的备件优化模型

张金风，夏桂梅，张文林

(太原科技大学应用科学学院，太原 030024)

基于MIMIC算法的备件优化模型

张金风，夏桂梅，张文林

(太原科技大学应用科学学院，太原 030024)

备件是系统能够完成任务的重要保障，是影响系统可靠度的重要条件，结合当前备件优化的工程需求，建立了基于分布估计算法的备件优化模型，利用Minmax思想将备件约束优化问题转化为无约束备件优化问题，并利用双变量相关MIMIC算法求解备件的最优配置。数值实验表明，提出的算法能有效地解决备件优化问题，且与其他算法进行比较，该算法能在满足系统任务可靠度时，得到较少费用的最优配置。

可靠度;备件优化模型;最优配置;MIMIC算法

备件的最优配置是系统能够完成任务的重要保障，根本目的是在有限费用情况下，寻找最优配置，使得系统任务可靠度最高，且能够满足最低要求的可靠度。

近些年，许多学者在备件优化方面做了很多研究。文献［1］对备件优化理论进行研究分析;文献［2］对系统完好率模型进行研究分析;文献［3-4］建立了基于微粒群算法的系统备件优化模型;文献［5-8］建立了基于遗传算法的系统备件优化模型，给出了求解该模型的具体步骤。从现有的文献中可以发现，这些求解备件优化配置问题，需要设置参数交叉率，变异率，惯性权重等，参数较多，而这些参数的选取没有统一的标准。MIMIC算法是一种新型的基于解空间分布模型的进化算法［9］，不需要设置这些参数，对目标函数和备件约束条件没有连续和梯度的要求。文章利用Minmax思想将备件约束优化问题转化为无约束备件优化问题，并利用双变量相关MIMIC算法求解备件的最优配置。

1 备件优化模型

1.1 设备可靠度要求

可靠度［10］指系统在规定的条件下和规定的时间区间内，完成规定功能的概率，记为R(t)，则有:

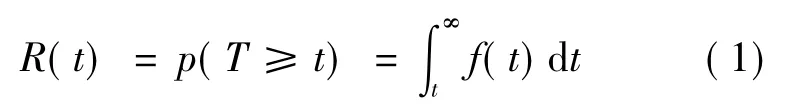
产品丧失规定的功能称为失效。产品从开始工作到失效前的一段时间T是产品能够正常工作的时间段，称为产品寿命。设寿命T的分布函数为F(t)，则:

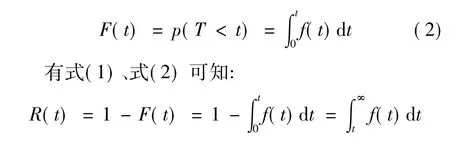
系统备件的可靠度取决于系统每个单元的可靠度，为了模型的建立，文章将整个系统看作是串联的转换开关完全可靠的冷贮备系统，所谓冷贮备系统指贮备单元在贮备时间内不发生失效，转换开关完全可靠指的是开关的可靠度为1的系统。

设系统设备共有m个部件，第i个部件有n个备件，且备件相同，则这种冷贮备系统的第i个部件的可靠度［10］为:

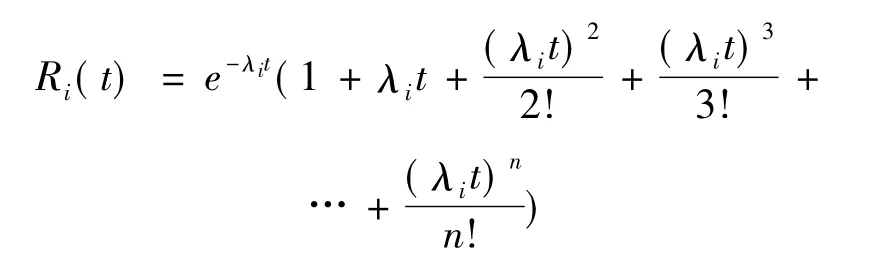
因为串联系统只有所有的部件都正常工作时，系统才正常工作，所以系统的可靠度:

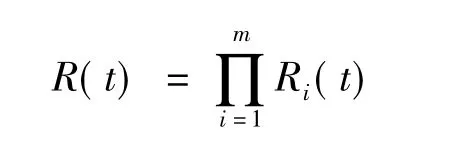
1.2 设备费用要求

系统备件的供应受到资金的影响，所以备件优化问题一定受到费用的约束。

1.3 模型的建立

文章讨论系统部件的备件数目和系统成功完成任务的可靠度的关系，则有下面三类备件优化模型:

模型1:系统任务可靠度为研究目标函数，费用为备件约束条件，既在费用有限情况下，使得系统任务可靠度最大。

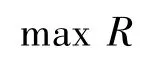
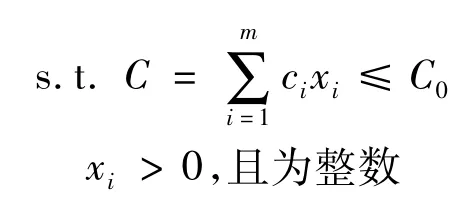
其中，xi为备件的数目，ci为第i种备件的单价，m为部件的种类，C为购买备件的总费用，C0为购买备件的最高花费。

模型2:费用为问题的目标函数，系统任务可靠度为备件约束条件，既在满足系统任务可靠度的约束情况下，使得花费最少，即购买费用最低。

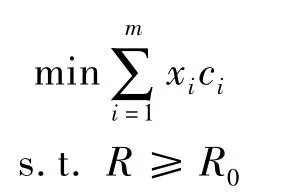
其中，xi，ci同模型1，R0为系统任务可靠度的最低要求。

模型3:以系统任务可靠度和费用的比值为问题的研究目标函数，系统任务可靠度和费用为备件约束条件，既在有限资金条件下，达到最低要求的可靠度。

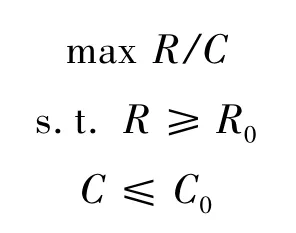
2 基于MIMIC算法的备件优化模型算法(Mx-MIMIC)

2.1 MIMIC算法

MIMIC算法是双变量相关的分布估计算法的一种，是由美国MIT人工智能实验室的De Bonet［11］等人于1997年提出的一种启发式优化算法。在MIMIC模型中，各变量是一种链式关系，解空间的概率模型为:

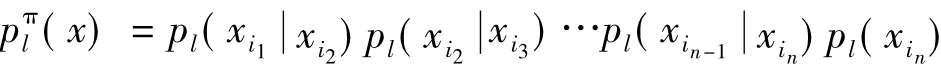
衡量两个概率分布之间的距离，可以用K-L距离，定义如下:

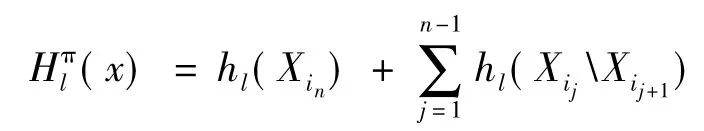
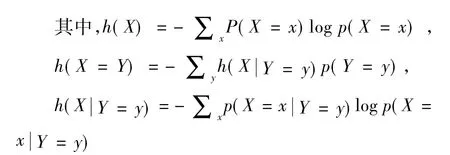
K-L距离是否足够小，只有足够小才能说明优势群体估计出的概率模型与真实的分布是非常一致或是接近，所以寻找最优的排列π*使K-L距离最小化。为了不把所有的n!个可能排列都穷举，本文利用贪心算法［11］来搜索变量的近似最优排列。

在MIMIC算法中，每一次迭代，都要根据选择的优势群体建立概率模型然后由抽样产生新的群体。其基本思想是按照π*的逆序，对第in，in-1，，i1个变量依次采样，构造一个完整的解向量，步骤如下:

(1)j=n，根据第ij个变量的概率分布pl(xij)，随机采样产生第ij个变量;

(2)根据第ij-1个变量的的条件概率分布，随机采样产生第ij-1个变量;

(3)j=j-1，如果j=1，则一个完整的解向量构造完成，否则转(2).

2.2 Minmax法

Minmax［12］定义:

备件约束问题:

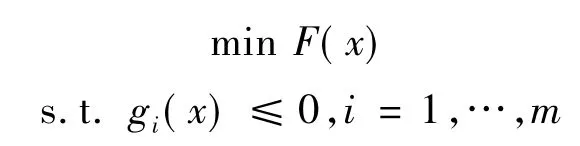
无约束备件问题:

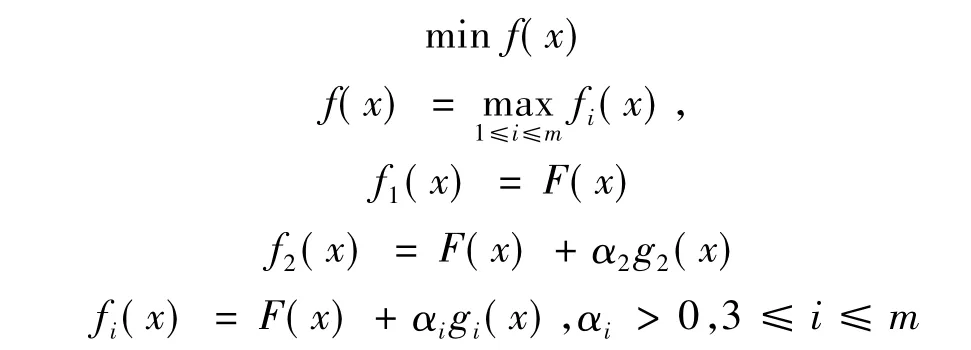
可以证明［12］上述约束问题对充分大的αi等价于无约束问题。该种策略，给予违反备件约束条件的迭代点很大的目标函数值，迫使一系列无约束备件优化问题的极小点无限地靠近最优方案，直至迭代点收敛到原问题的最优方案。同时，Minmax法可以处理多个线性或非线性约束条件。

2.3 Mx-MIMIC算法具体步骤

具体步骤如下:

(1)初始群体，随机产生N个个体pop0，k→0;

(2)利用Minmax算法法将备件约束问题转化为无约束备件问题;

(3)计算群体中每个个体的适应值，如果符合所设置的终止条件，算法结束，否则算法继续进行迭代;

(4)用截断和轮盘赌选择M＜N个个体作为优势群体，并保留最优个体p个;

(5)根据贪婪算法寻找最优排列而建立优势群体的概率模型;

(6)按逆序从概率模型中采样m次，与p个最优个体形成新一代群体popk+1，转3.(m=N-p)

3 Mx-MIMIC算法实例与分析

3.1 算例1

以某型弹药装备系统，该系统有4类型的主要部件［13］，其对应的备件单价和故障率如下表1.

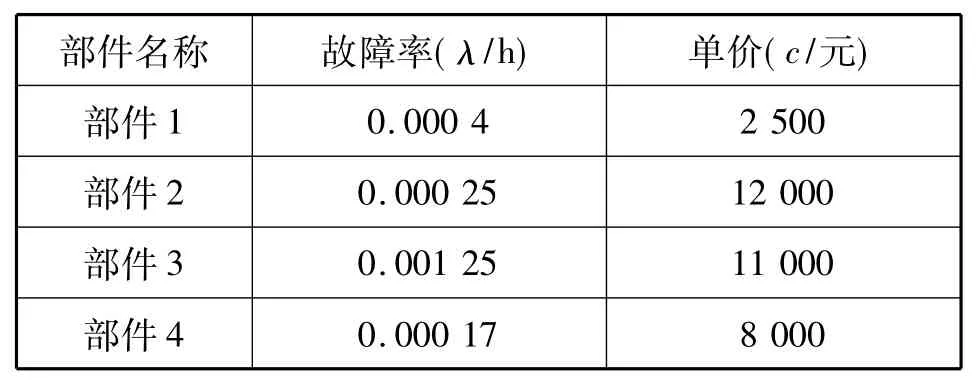
表1 弹药装备备件参数表Tab.1 Parameters of spare parts for missile equipment

其中要求费用最多为100 000元，工作时间为1 500 h，系统可靠度最低要求0.9.

该算例1选取备件优化模型3，备件优化模型:

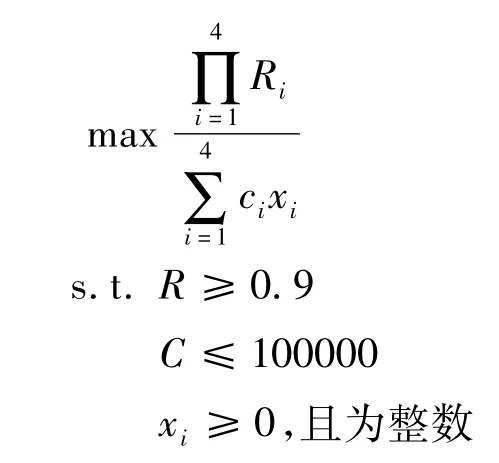
3.1.1 试验结果

参数设置:群体规模2 000，精度为10-6，进行10次仿真试验，α1=1 000，α2=100，贪焚算法迭代次数200，优势群体个数1 000.数值测试结果和进化代数进行统计，并分析结果，如表2.

从表2中可以发现Mx-MIMIC算法和遗传算法都可以找到最优配置，满足系统可靠度最低要求，但是Mx-MIMIC算法找到的最优配置比遗传算法的最优配置的费用低了4 000元。同时，Mx-MIMIC算法的进化代数为25，而遗传算法进化代数为64，说明Mx-MIMIC算法进化速度快，提高了仿真试验效率。

表2 Mx-MIMIC算法和遗传算法性能比较Tab.2 Comparison results for the Mx-MIMIC algorithm and GA algorithm

表3 可靠度约束条件对结果的影响Tab.3 The effect of reliability constraints on resuits

表4 装备备件参数表Tab.4 Parameters of spare parts

3.1.2 可靠度约束条件对结果的影响

在仿真实验中，发现随着备件约束条件可靠度R0的增大，可以最大限度地利用费用，提高费用利用率。令系统约束可靠度R0从0.9开始，按0.01递增，直到0.99，共10组参数。结果发现，随着系统可靠度增大，可以最大限度提高费用利用率，但可靠度不能无限增大，系统可靠度达到0.956 1已经最大，结果如表3.

3.2 算例2

某系统中影响系统可靠度的最重要部件有10种［14］，对应的备件单价和故障率如下表4，要求费用为100万元限制下，求备件的最优配置使得系统可以工作600 h的可靠度最大。

该算例2选取备件优化模型1，备件优化模型:

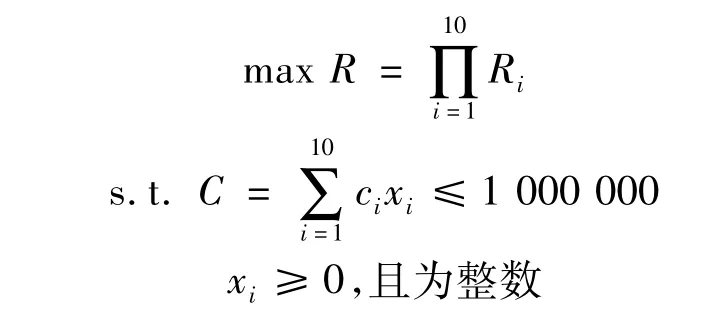
3.2.1 试验结果

参数设置:群体规模5 000，精度为10-6，进行5次仿真试验，α1=1 000，贪焚算法迭代次数为200.对数值测试结果进行统计，并分析结果，结果如表5.

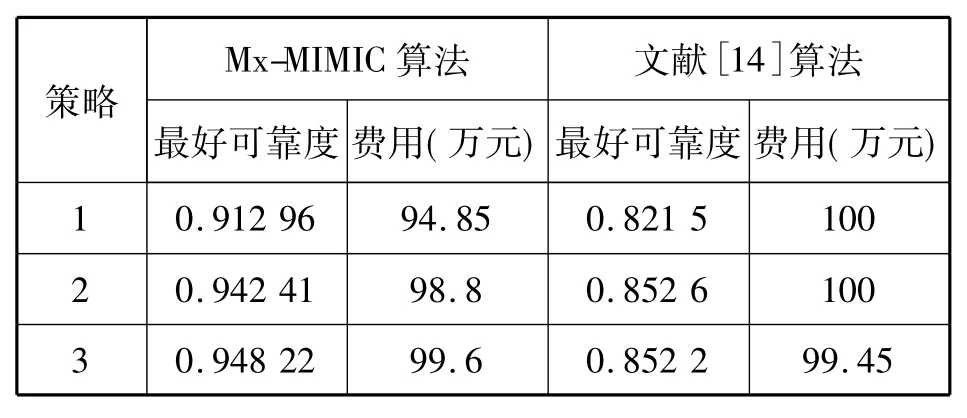
表5 Mx-MIMIC算法和文献［14］算法性能比较Tab.5 Comparison results for the Mx-MIMIC algorithm and reference algorithm

其中，策略1为每25组个体选择1组作为母本，策略2为每50组个体选择1组作为母本，策略3为每100组个体选择1组作为母本。

Mx-MIMIC算法在三种策略中得到最优配置方案为(2，4，5，1，3，4，3，4，2，4)，装备系统最好可靠度为0.948 22.算法在不同策略下所找到的最优配置使得系统可靠度都比文献14的系统可靠度高，同时满足费用约束条件。说明本文所求得的最优配置方案既使得系统可靠度较高，也满足了资金100万元的约束条件，有一定的优势。

3.2.2 费用约束条件对可靠度的影响

固定群体规模，令备件约束条件费用从250 000元开始，按50 000元递增，直到1 000 000元，共16组参数。结果发现，在费用低的情况下，费用约束条件对试验结果有影响且差异大，在250 000到600 000之间，所得配置方案的可靠度太低，且没有满足费用约束条件，在费用较高情况下，特别费用从650 000到10 000 000之间，系统可靠度是随着费用增加而上升的趋势，同时，满足费用的约束条件，使得费用得到合理利用，结果如表6.

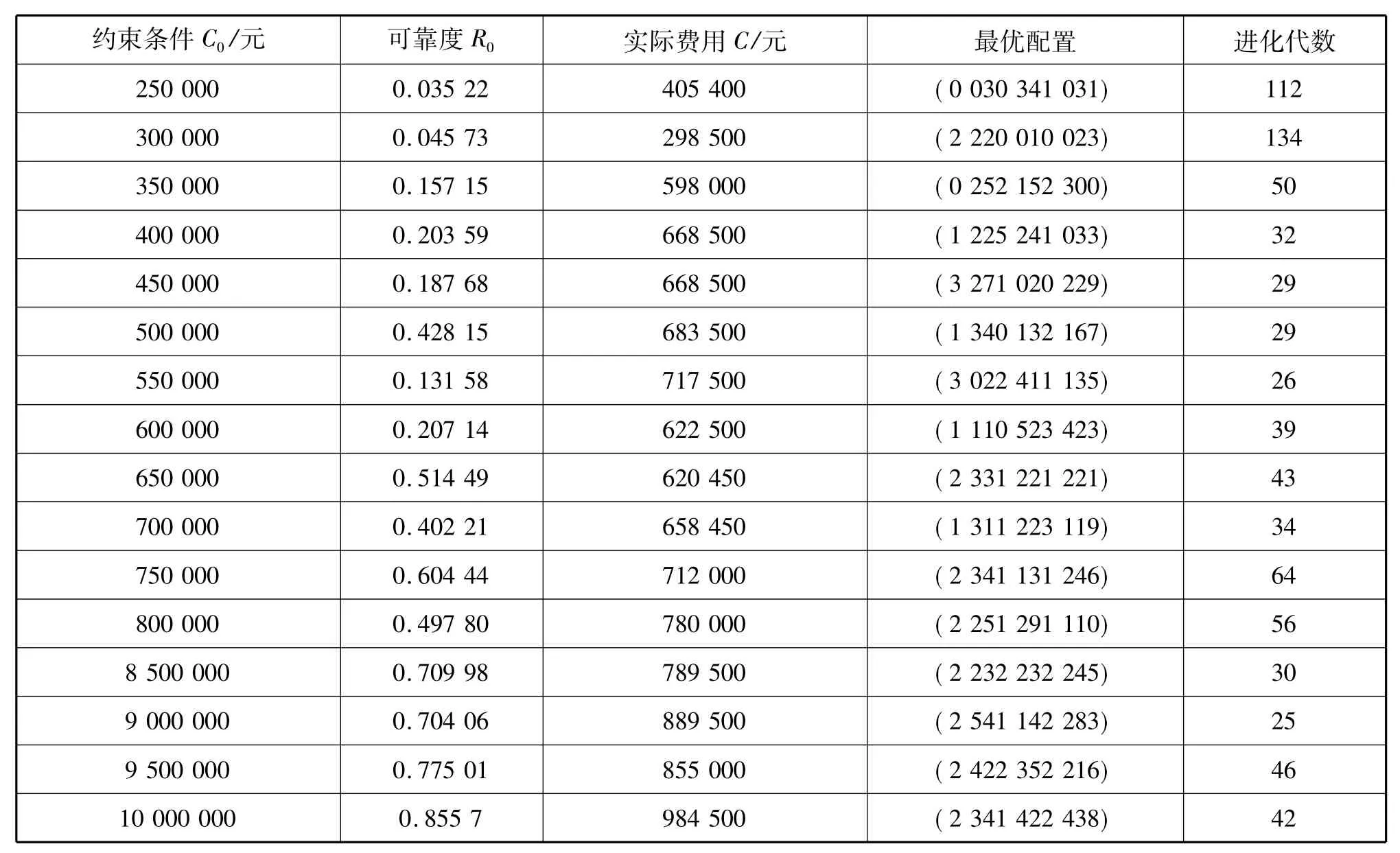
表6 费用约束条件对结果的影响Tab.6 The effect of cost constraints on resuits

4 结束语

(1)文章改进的Mx-MIMIC算法可以对装备备件优化配置问题求解，且结果良好。

(2)备件模型的约束条件对求解系统可靠度有很大影响，算例1说明了备件约束条件可靠度的增加可以提高费用利用率，算例2说明了在费用较高情况下系统可靠度是随着费用增加而上升的趋势，满足费用的约束条件，使得费用得到合理利用。

［1］张蕊，袁立峰，汪凯蔚.备件优化理论分析与应用研究［J］.装备环境工程，2012，9(5):52-54.

［2］李建伟，郭基联，王卓健.概率分布模型的飞机战备完好率评估与预测［J］.活力与指挥控制，2011，36(10):74-76.

［3］刘勤明，吕文元.PSO算法在设备备件优化配置模型研究中应用［J］.矿山机械，2009，37(2):33-34.

［4］郑小丽，黎放，狄鹏.整数规划PSO算法在备件优化配置中的应用研究［J］.舰船电子工程，2009，29(3):133-135.

［5］苑立伟，赵英俊，陈永革.防空导弹武器装备备件优化模型［J］.现代防御技术，2002，35(5):13-16.

［6］李世英，陈乐，于永乐，等.基于GA的维修设备备件优化配置模型研究［J］.科学技术与工程，2006，6(24):3928-3930.

［7］熊强强，方强，吴军.基于遗传算法的备件配置优化方法［J］.四川兵工学报，2014，35(5):54-57.

［8］王永川，蔡金燕，曹宏炳.基于遗传算法的雷达功能板备件优化模型［J］.现代雷达，2002，24(4):1-3.

［9］周树德，孙增圻.分布估计算法综述［J］.自动化学报，2007，33(2):115-118.

［10］孙新利，陆长捷.工程可靠性教程［M］.北京:国防工业出版社，2005.

［11］DE BONET J S，ISBELL C L，VIOLA P.Finding optima by estimating probability densities［J］.Advances in Neural Information Processing Systems，1997(9):424-430.

［12］PARSOPOULOS K E，VRAHATIS M N.Recent Approaches to Global Optimization Problems through Particle Swarm Optimiza-tion［J］.Natural computing，2002，1(2):275-282.

［13］潘广泽，高军，黄道平，等.基于遗传算法的弹药装备备件优化模型研究［J］.可靠性与环境适应性理论研究，2014，32 (8):12-15.

［14］刘新亮，张涛.基于分布估计算法的备件优化配置［J］.系统工程理论与实践，2009，29(2):147-148.

Model of Spare Parts Optimization Based On MIMIC Algorithm

ZHANG Jin-feng，XIA Gui-mei，ZHANG Wen-lin
(School of Applied Science，Taiyuan University of Science and Technology，Taiyuan 030024，China)

Spare parts play an important role for the system to complete task，and have much influence on system reliability.In this paper，the model of spare parts optimization based on estimation of distribution algorithms is proposed for the need of current project，the constrained optimization problems of spare parts are transformed into unconstrained optimization problems of spare parts through Minmax algorithm，then the MIMIC algorithm is applied to solve the optimization configuration of spare parts.The simulation results show that the proposed algorithm can solve the spare parts optimization problem，and the optimization configuration of spare parts of the algorithm can satisfy the system reliability with less cost when comparing with other algorithms.

reliability，model of spare parts optimization，optimization configuration，MIMIC algorithm

0221

A

10.3969/j.issn.1673-2057.2015.02.015

1673-2057(2015)02-0154-06

2014-11-24

山西省自然科学基金项目(2014011006-2)

张金风(1986-)，女，硕士研究生，主要研究方向为最优化理论及其应用。