复杂生物膜动力系统的显式有限差分方法研究
2015-06-23孙高峰牛瑞萍
孙高峰,牛瑞萍,李 明
(太原理工大学 数学学院,太原 030024)
复杂生物膜动力系统的显式有限差分方法研究
孙高峰,牛瑞萍,李 明
(太原理工大学 数学学院,太原 030024)
针对刻画生物膜成长的动力系统设计了一个非负、有界的显式差分格式,系统是由四个变系数的非线性抛物型偏微分方程组成,描述了营养基质上多种微生物成分间的交互过程;所设计的有限差分格式巧妙地将非线性项转化成线性形式,确保得到的数值解是非负、有界的。最后通过两个数值算例检验了方法的性能,并给出了宏观意义下的数值解的误差。
复杂生物膜系统;非线性反应扩散方程组;显式有限差分法;非负、有界
在科学计算中经常要用数值求解各类微分方程[1],有限元[2-3]、有限差分法[6-8]和有限体积法[4-5]是最重要的常用方法。本文使用有限差分法求解生物膜系统的数值解.生物膜系统本身物理属性要求数值解是非负、有界的,因此,设计非负、有界的有限差分技术已成为计算数学的重要研究领域[6-8]。
Eberl et al建立的抛物型偏微分方程组来描述复杂的生物系统与周围营养基的相互作并证明了该问题在合理的解析约束下,非负、有界解的存在唯一性[9-11]。受Eberl所做工作的启发,目前的工作主要是制定一种新的显式有限差分法来有效地求解非线性抛物型偏微分方程组。由于生物膜系统是具有实际意义的体系,其未知变量表示各种微生物及营养成分的密度,是非负、有界的变量。如何设计一个有效的差分格式确保数值解的非负、有界性尤为重要。通常的生物系统的扩散系数是给定非负常数,这样的系统设计数值计算相对容易,文献中[6-11]已有许多成功的方法,但Eberl et al的生物系统的扩散系数是未知变量的函数,使得控制方程组是一个非线性的变系数偏微分方程组,这增加了设计数值计算方法的难度;本文的主要内容是在初边值条件下对复杂生物膜系统显式有限差分方法进行研究。
1 生物背景及数学模型
复杂生物膜系统由下面四个非线性偏微分方程确定:
(1)
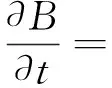
(2)
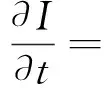
(3)
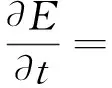
(4)
M(X,t)=B(X,t)+I(X,t)+E(X,t) .
(5)
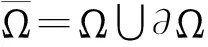
本文,假定μ,kL,kE,kI,kS,YE为非负常数,YH正常数,这些所有的常数均是通过实验获得的。和·分别表示空间梯度算子和散度算子。S表示关于最大值标准化后营养浓度;函数M(X,t)表示问题域上的系统生物质量密度。复杂生物膜系统中包含种类型的微生物:B表示活的微生物密度;I表示惰性或死的微生物密度;E表示胞外聚合物密度,这三个变量是关于最大量标准化的得到的量。显然,对于和M∈[0,1)。从生物学角度看,偏微分方程组(1)-(5)刻画的是不同生物之间以及生物和营养基之间的相互交互转化过程。函数D(u)描述生物演化动力学(生长、衰减、繁衍)规律的非线性扩散系数,通常是微生物的函数,因此它是非线性的“根源”,本章使用下列形式的扩散系数:
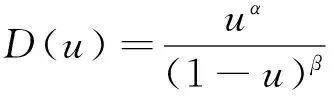
式中,α≥1,β≥1.
方程(1)刻画的是生物膜上的营养的消耗和转化,值得注意的是活的微生物和胞外聚合物是营养的潜在“源”(可以转化成营养),右端的第三和第四项刻画的是转化机制。这里,正常数kL表示活生物转化为营养物的效率;正常数kE表示胞外聚合物转化成营养物的效率;右端第一项营养物的扩散项;右端第二项是标准的Monod-type函数,描述的是活生物如何消耗营养物.参数μ表示活生物的最大增长率;参数1/YH表示活生物消耗营养率。
方程(2)刻画了生物膜上活生物的增长和转。右端第一项控制活生物的扩散;第二项是标准的Monod-type函数,描述的是营养物如何促进活生物的增长;第三和第四项描述了活生物如何转化成营养物和惰性生物;正常数kI表示活生物转化成惰性生物的效率。
方程(3)右端的第一项控制惰性生物的扩散,第二项表示活生物如何促进惰性生物的增长。
方程(4)描述的是胞外聚合物的消耗和转化。方程右端的第一项控制胞外聚合物的扩散;第二项描述的活生物如何促进胞外聚合物的增长;常数YE表示胞外聚合物消耗活生物的效率。
2 有限差分方法
下面我们给出由方程式(1)-(5)所控制复杂生物膜系统的显式非负、有界差分逼近形式。设问题域为正规的时-空区域:
(x,y,t)∈[0,X]×[0,Y]×[0,T] .
控制方程(1)-(4)的扩散项可统一表示成下列方程:
·(D(M)f)=D(M)xfx+
D(M)yfy+D(M)(fxx+fyy) ,
式中:函数f依次可代表S,B,I,E。
下面我们使用以下有限差分形式对系统进行近似:
δxxf=
δyyf=
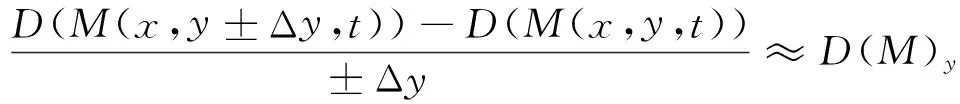
为简化记号,我们令

下面给出控制方程(1)-(4)式中扩散项的逼近形式为:
·(D(M)f)≈
其中,函数f依次可代表S,B,I,E。为进一步简化记号,令
因此,复杂的生物膜系统(1)-(4)可由下面有限差分近似:
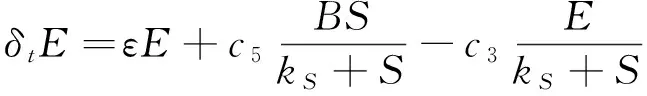
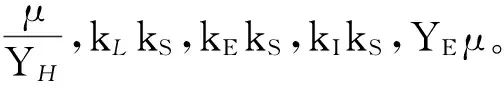
3 离散有限差分格式
为了表述的方便,下面给出一维模型的有限差分格式。
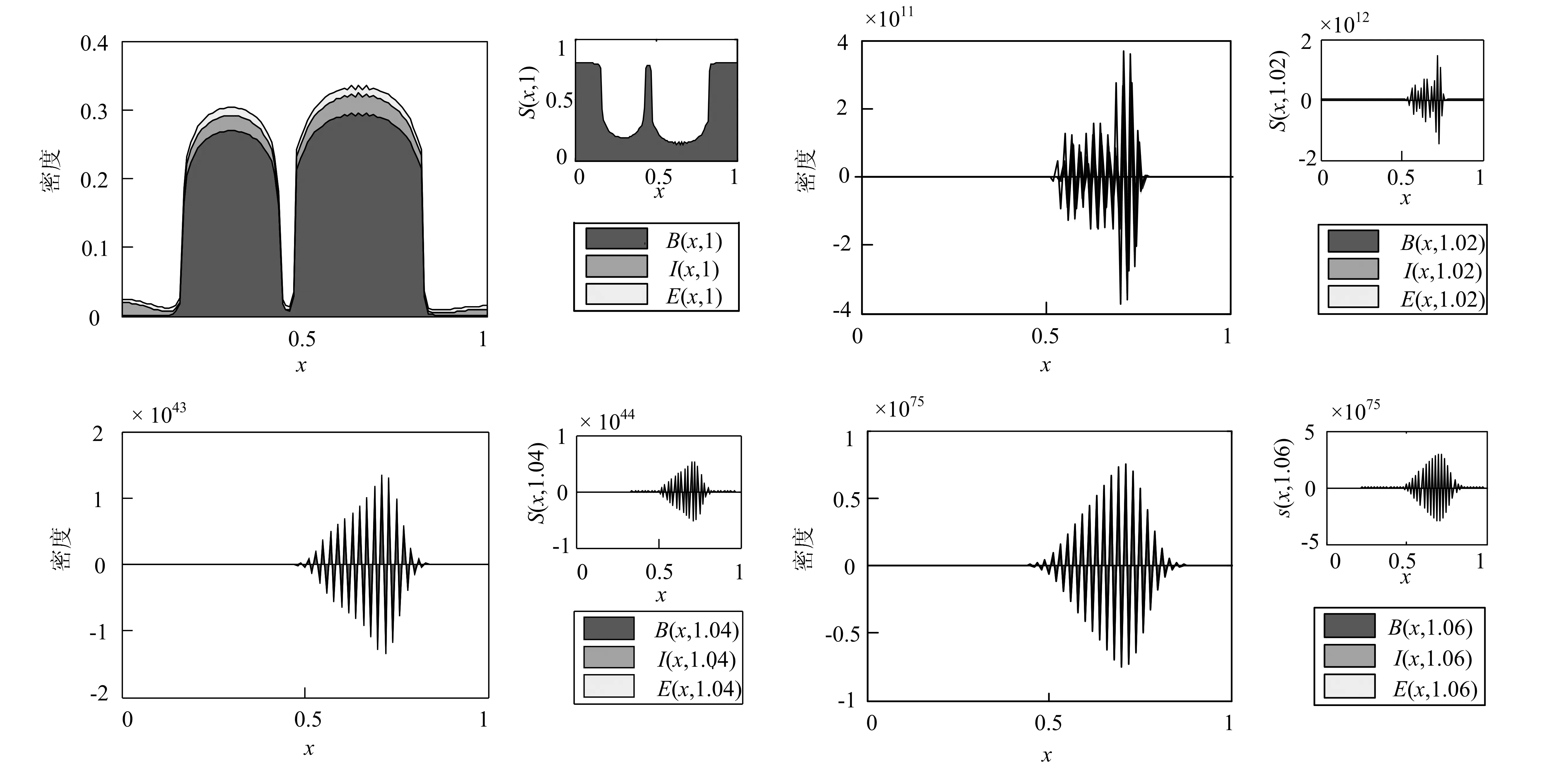
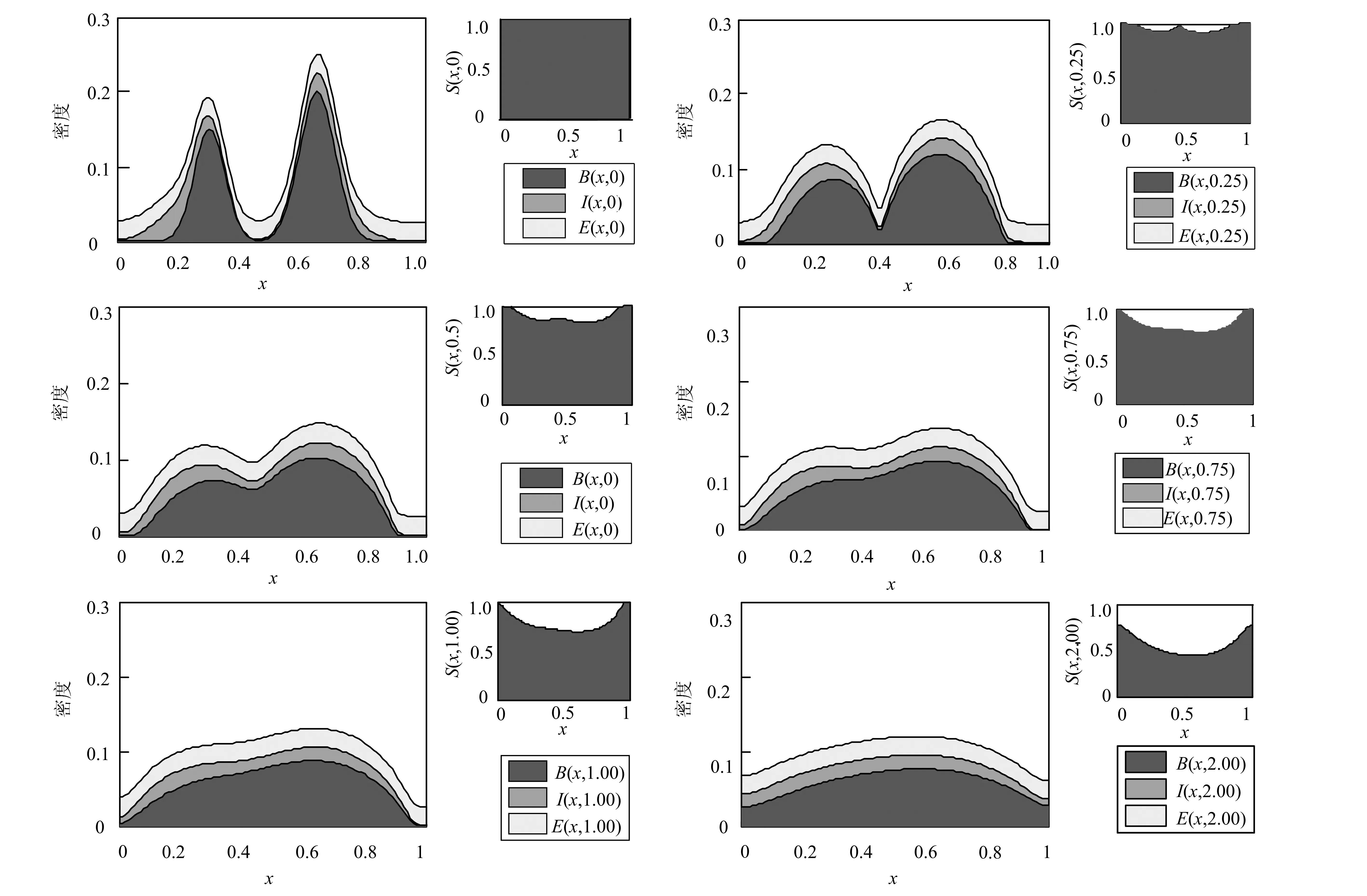
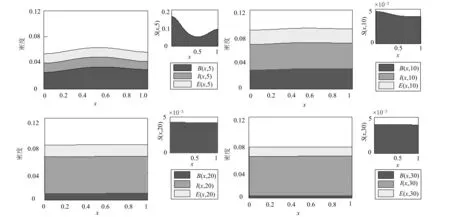
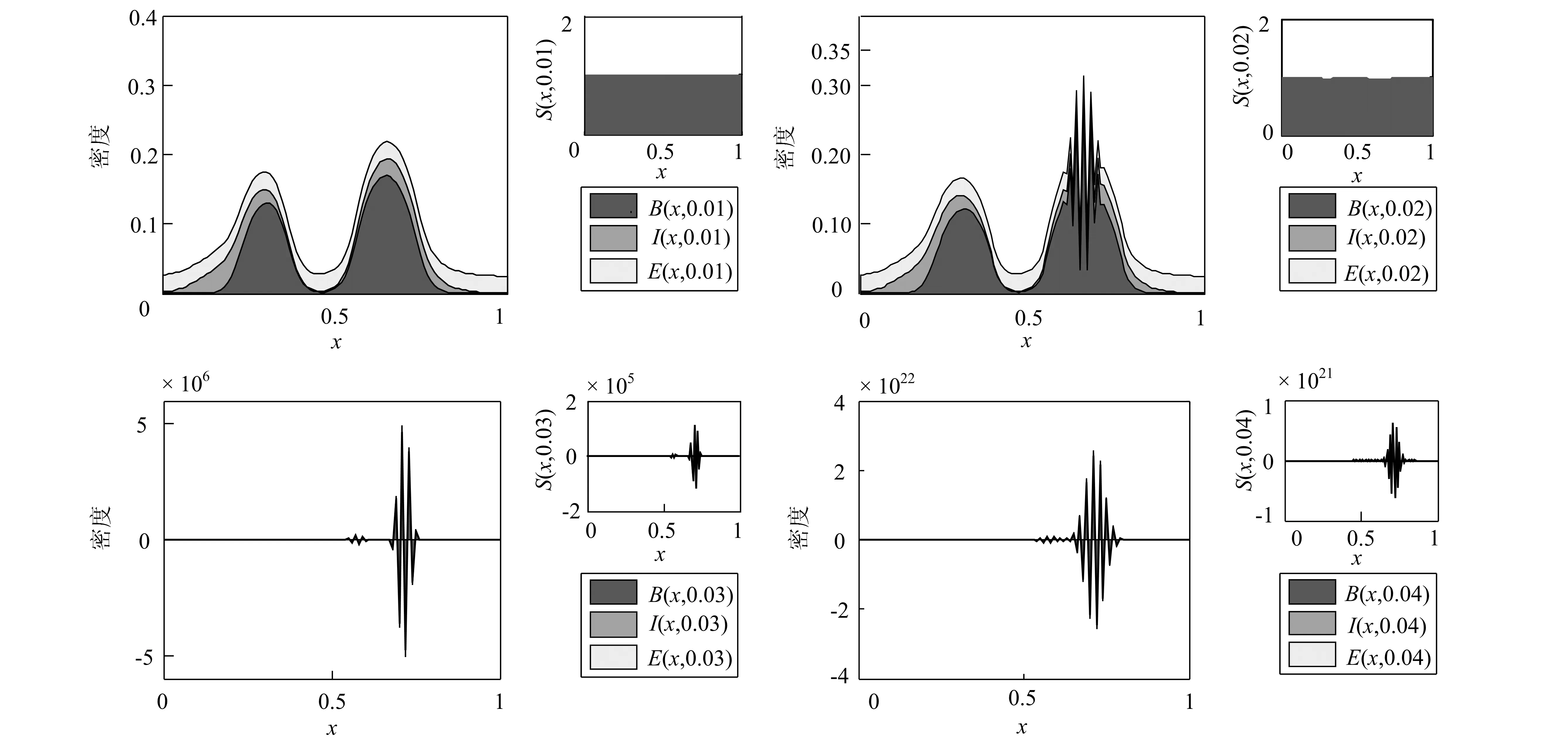
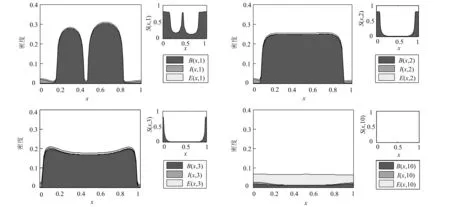
设a,b为实数,且a xi=(i-1)Δx. i=1,2,3,…,M+1,且Δx=(b-a)/M.tk=(k-1)Δt.k=1,2,3,…,P+1,且Δt=T/P. (6) (7) (8) (9) (10) 为了说明所提出的有限差分格式的优越性,下面给出另外一种标准中心有限差分格式: (11) (12) (13) (14) 这里 下面根据系统定义边界为Neumann边界条件的系统宏观误差。 联立系统方程(1)-(5),有: (15) 将上式方程在域(x,y,t)∈[0,X]×[0,Y]×[0,t]上积分,得到下列积分方程形式: 式中:b1=μc2,b2=(c1-c5)c2,b3=(c1-c5)(c2+c4)-μc2,b4=μc4. 进一步简化记号,令 这样方程(15)可以改写成下列形式: b1(St-S0)+b2(Bt-B0)+ b3(It-I0)+b4(Et-E0)=0 . 因此,宏观误差Em可定义为下列形式: Em=|b1(SNt-S0)+b2(BNt-B0)+ b3(INt-I0)+b4(ENt-E0)| . (16) 这里, SN(x,y,t),BN(x,y,t),IN(x,y,t)及EN(x,y,t)依次表示营养物浓度、活生物密度、死生物密度及胞外聚合物密度在点(x,y,t)处的数值解。 算例1 计算使用的参数μ=0.02,YH=0.003,YE=KE=0.03,KS=0.2,KI=0.04,KL=0.04;α=β=2,问题域为Ω=(0,1),控制方程为(1)-(5),初始条件为: S0(x)=1 , B0(x)=0.15e-200(x-0.3)2+0.2e-150(x-0.65)2, I0(x)=0.04e-80(x-0.2)2+0.03e-60(x-0.7)2, E0(x)=0.025 . 在边界网格点上施加均匀的Neumann边界条件,使用的网格为Δt=0.001 and Δx=0.01,数值结果如图 1所示。 图1 使用有限差分格式(6)-(9)得到的数值解 由式(16)计算出的5个时刻t=0.25,0.5,0.75,1,2的宏观误差依次为: 1.589 9×10-4,1.368 3×10-4, 1.131 9×10-4,8.583 0×10-5,3.162 4×10-4. 图2给出的是4个不同时刻t=5,10,20,30的数值解。相应的宏观误差依次为:2.685 6×10-5,2.180 2×10-6,9.097 0×10-5,1.178 6×10-4.在这种长期情况下,营养基质函数是趋于零的,而活微生物扩散到整个空间区域。对于长时间的行为,进一步的实验证实活的微生物密度最终趋于零,这也是我们所期望的。 综合图 1和图2,我们发现,起初随着营养基质密度的减小,总的微生物量有所增加,随着时间的增加,活性微生物转化成惰性微生物。 从图3可以观察到,使用有限差分格式(11)-(14)得到的数值解具有奇异性和震荡现象,说明该格式不稳定,不能确保数值解是非负、有界的。而本文提出的有限差分格式是稳定的,得到的数值解是非负、有界的。 算例2 计算使用的参数μ=2,YH=0.35,YE=KE=0.03,KS=0.2,KI=0.4,KL=0.001;α=β=4,问题域为Ω=(0,1),控制方程为(1)-(5),初始条件为: S0(x)=0.8, B0(x)=0.15e-200(x-0.3)2+0.2e-150(x-0.65)2, I0(x)=0.02e-80x2+0.01e-60(x-1)2, E0(x)=0.005 . 在边界网格点上施加均匀的Neumann边界条件,使用的网格为Δt=0.001 and Δx=0.01,数值结果见图4。 图4给出了4个不同时刻t=1,2,3,10的数值解.相应的宏观误差依次为:1.765 1×10-6,6.717 4×10-6,3.037 0×10-6,可以观察到,在起初阶段,随着营养基质函数的减小,活微生物密度总量增加;当营养基质趋于零时,活微生物密度总减小,逐渐趋于零;而对惰性生物密度总量始终是增加的。这些结果符合系统的特征。 图2 使用有限差分格式(6)-(9)得到的数值解 图3 使用有限差分格式(11)-(14)得到的数值解。使用的控制方程、初始条件、边界条件、计算参数以及计算网格和图 1和图2相同 图4 使用有限差分格式(6)-(9)得到的数值解 从图5可以观察到,对数值算例2使用有限差分格式(11)-(14)得到的数值解也具有奇异性和震荡现象,说明该格式不稳定,不能确保数值解是非负、有界的.而本章提出的有限差分格式是稳定的,得到的数值解是非负、有界的。 本文用新的显式有限差分法来逼近复杂生物膜系统的正的、有界解,其控制方程是由四个抛物线型偏微分方程构成,偏微分方程中同样也包含一个与密度相关的非线性扩散反应项.理论上,模型的非负、有界解的存在性和唯一性文献中已有证明,而获得该模型的精确解确实是很困难的,因此,我们不得不采用数值模拟的方法来得到近似解。本文的理论和数值研究总结如下: 1) 建立了复杂生物膜系统的显式有限差分格式; 2) 给出了2个数值算例,结果表明数值结果和实际是相吻合的,能够反应微生物成长规律; 3) 和标准中心差分方法相比较,本文所提出的方法具有较好的稳定性,不会出现奇异的数值解和震荡现象; 4) 不足之处,相关收敛性、稳定性等理论体系还没建立起来。 图5 使用有限差分格式(11)-(14)得到的数值解。使用的控制方程、初始条件、边界条件、计算参数以及计算网格和图4相同 [1] 李治平.偏微分方程数值解讲义[M].北京:北京大学出版社,2010. [2] Liu WK,Liu YL,Farrell D.Immersed finite element method and its applications to biological systems[J].Computer Methods In Applied Mechanics And Engineering,2006,195(13-16):1722-1749. [3] Liu G R,Quek S S.Finite Element Method:a practical course[M].Burlington MA:BH,2003. [4] Wang Shuai,Yuan Guangwei,Li Yonghai.A monotone finite volume scheme for advection-diffusion equations on distorted meshes[J].International Journal for Numerical Methods in Fluids,2012,69(7):1283-1298. [5] Hermeline F.A finite volume method for the approximation of convection-diffusion equations on general meshes[J].International Journal For Numerical Methods In Engineering,2012,91(12):1331-1357. [6] Macías-Díaz J E.A bounded finite-difference discretization of a two-dimensional diffusion equation with logistic nonlinear reaction[J].Int J Mod Phys C,2011,22:953-966. [7] Macías-Díaz J E,Jerez-Galiano S,Puri A.Positivity-preserving methods for a linearized Fisher-KPP equation with consistency properties in the energy domain[J].J Differ Equ Appl,2010,16:389-405. [8] Macías-Díaz J E,Puri A.A boundedness-preserving finite-difference scheme for a dampednonlinear wave equation[J].Appl Numer Math,2010,60:934-948. [9] Eberl H J,Parker D,van Loosdrecht M C M.A new deterministic spatio-temporal continuum model for biofilm development[J].J Theor Med,2001,3:161-176. [10] Efendiev M A,Eberl H J,Zelik S V.Existence and longtime behavior ofsolutions of a nonlinear reaction-diffusion system arising in the modeling of biofilms[J].RIMS Kokyuroko,2002,1258:49-71. [11] Eberl H J.A deterministic continuum model for the formation of EPS in heterogeneous boilarchitectures[J].Proc Biofilms,2004,237-242. (编辑:朱 倩) Explicit Finite-difference Method for a ComplexBio-film Dynamics System SUN Gaofeng,NIU Ruiping,LI Ming (CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China) Numerical methods with non-negative and bounded solutions have great significance because of the requirement from many mathematical models with practical background.In this paper,a non-negative and bounded explicit finite-difference scheme is presented for bio-film growth dynamics system.The scheme describes mutual process among different microorganism compositions on nutritional substance and is expressed by four nonlinear parabolic partial differential equations with variable coefficients.The explicit finite-difference scheme neatly transforms the nonlinear form into linear form,which ensures the non-negative and bounded property of solutions.Numerical examples are presented to illustrate the performance of the methods.Error in macro significance is also given. complex biofilm dynamics system;explicit finite-difference method;nonlinear reaction-diffusion equations;Nonnegative bounded 1007-9432(2015)06-0790-07 2015-04-09 国家自然科学基金资助项目:可商业化光滑有限元分析软件的研发(11472184) 孙高峰(1976-), 男,山西临猗人,博士,主要从事计算数学的研究,(Tel)13453157694 李明(1982-),男,教授,主要从事无网络计算方法,偏微方程中的反问题等的研究,(E-mail)liming01@tyut.edu.cn O241 A 10.16355/j.cnki.issn1007-9432tyut.2015.06.028
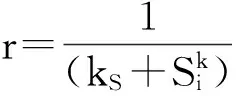
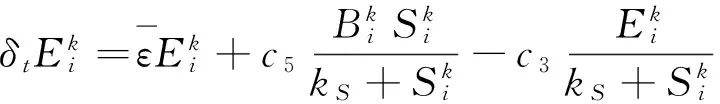

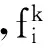
4 数值算例
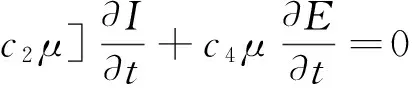
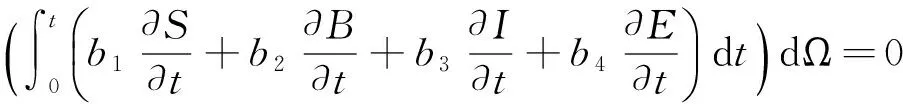
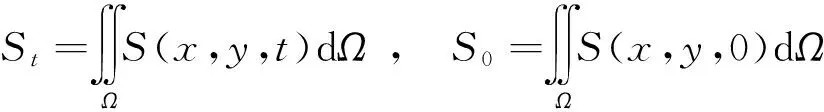
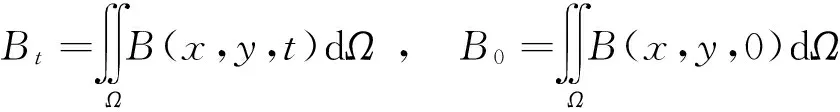
5 结论