基于相关性的OFDM盲识别与参数估计方法

张孟伯，杨晓静，张欣冉，樊斌斌

（1.电子工程学院，合肥 230037；2.安徽大学，合肥 230039）

基于相关性的OFDM盲识别与参数估计方法

张孟伯1，杨晓静1，张欣冉2，樊斌斌1

（1.电子工程学院，合肥 230037；2.安徽大学，合肥 230039）

针对非协作通信领域OFDM信号识别难的问题，提出一种基于信号循环前缀相关性的盲识别和时域参数估计算法。通过对OFDM信号循环自相关函数进行分析，在时域上求出延时自相关运算函数的波形，利用循环前缀的相关波峰的特性，以区别OFDM信号和单载波信号，实现对OFDM信号的盲识别。在此基础上，通过采用多个OFDM信号构造循环前缀相关性的累加函数所形成的波峰完成对符号和循环前缀长度等参数的估计。

OFDM，循环前缀，相关函数，盲识别，参数估计

0 引言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是一种高频谱利用率的多载波调制技术，具有很强的抗多径干扰、抗衰落能力，被相继应用到非对称的用户环路（ADSL）、ETSL标准的数字音频广播（DAB）、数字视频广播（DVB）、高清晰度电视（HDTV）和基于IEEE802.11标准的无线局域网（WLAN）中，成为了第四代移动通信中的核心技术［1］，在未来信息化战场中有着至关重要的作用。

对OFDM信号的盲识别和参数估计是非协作通信领域中的一项重要课题，如何在低信噪比和多径信道的战场环境下有效识别出OFDM信号，并对其相关参数进行估计，是对OFDM信号进行通信对抗研究所亟需解决的问题。文献［2］利用OFDM信号的渐进高斯性，采用高阶累积量作为识别特征参量完成了盲识别，但其计算复杂度高，且要求的信噪比较高，所以实用性不强；文献［3］在此基础上提出利用四阶累积量构造识别参数来区分OFDM信号与单载波信号，但需要预先知道载波的频率，并且需要在每个信噪比点的条件下设置相应的门限值，算法复杂；文献［4］结合非周期的齐次马尔可夫链模型，推导了OFDM信号的循环谱公式，从而为利用循环谱对0FDM信号进行盲处理奠定了理论基础，但只在理论层面进行分析，并未作出具体的识别和检测；文献［5］利用接收信号循环前缀的相关性，提出一种基于循环前缀的0FDM信号盲检测及参数估计算法，但需要预先对有效长度和循环前缀进行估计，在低信噪比时效果较差，并且没有考虑多径效应的影响；文献［6］算法不需要信号和噪声的先验条件，直接对中频信号进行处理，具有较强的实用性，但因加入了极大值提取的延时估计，增加了运算的复杂性，并未有效地提高了整体的识别率。

本文在现有文献研究的基础上，利用循环前缀的相关性，提出一种改进的可变偏移长度相关方法进行OFDM信号盲识别和参数估计，有效克服噪声和多径衰落对信号处理的影响，算法简单、识别准确率高，并且不受设计参数的限制，不需对有效长度和循环前缀做预估计，具有较高的实用价值。

1 OFDM信号特点的描述

正交频分复用（OFDM）的基本原理就是把高速的数据流通过串并变换，分配到传输速率相对较低的若干个子信道中进行传输，主要有以下特点［7］：

①子载波信道频谱相互正交，提高了频谱的利用率；

②子信道中的符号周期会增加，减轻由无线信道的多径时延扩展所产生的时间弥散性对系统造成的影响；

③在OFDM符号之间插入保护间隔，令保护间隔大于无线信道的最大时延扩展，最大限度地消除由于多径信道带来的符号间干扰（Inter Symbol Interference，ISI）。

目前，工程上一般采用循环前缀（Cyclic Prefix，CP）作为保护间隔，实现OFDM符号的循环扩展，具体做法是将OFDM符号后部的采样复制到其前面，以消除符号间干扰，结构如图1所示。

图1 OFDM信号结构图

由图1知，在OFDM信号中符号周期T=Tu+Tcp， Tu=Δfk-1表示有效符号的周期长度，Tcp表示循环前缀的长度，T的倒数表示信号的符号率。由于循环前缀是有效数据尾部的复制，所以OFDM信号在结构上就具有自相关性，本文主要根据循环前缀的所具有的相关性作为突破点，完成对OFDM信号的盲识别以及有效周期长度Tu、符号周期长度T等时域参数的估计。

2 OFDM信号的盲识别和参数估计方法

发送信号s（t）在噪声环境下经过多径信道后可表示为［8］：

其中hx表示不同路径的增益，x表示不同路径的时延，w（n）表示加性高斯白噪声，s（n）表示本文即将展开研究的信号模型。这里主要分析单载波信号ssc（ldn）和OFDM信号sofd（mn）的特点［9］。

其中a是未知的幅度，θ是初始的相位，Δfc是载波频率，T是符号周期，0≤ε≤1是定时误差，g（n）是均方根升余弦成形脉冲，K是OFDM信号的子载波数，Δfk是OFDM信号中相邻两个子载波的频率间隔，sl是单载波调制信号发射端在第l个时刻的传输符号，sk，l是OFDM调制发射端在第l个时刻第k个子载波上的传输符号，信号序列{sl}和{sk，l}均对应星座图上的点，服从独立分布。

2.1 OFDM信号的盲识别

由于循环前缀是对末尾有效数据的复制，因此，循环前缀和有效数据的末尾部分数据具有相关性，定义一个自相关函数为：

式（4）表示数据r（n）与数据r（n+k）相关值的和，由于存在偏移的最大值为K，所以N个数据只有N-K个数据参与运算，把式（1）～式（3）带入式（4），由于噪声和数据信号相互统计独立，之间不具相关性。实际应用中，为了有效降低多径时延扩展所产生的频率选择性衰落对系统造成的影响，OFDM信号的循环前缀Tcp一般大于路径时延x，因此，在本文的以下的自相关函数推导中假设各路径的hx以及x近似不变。

当循环前缀和它的复制源进行相关运算时，将得到峰值公式［10］：

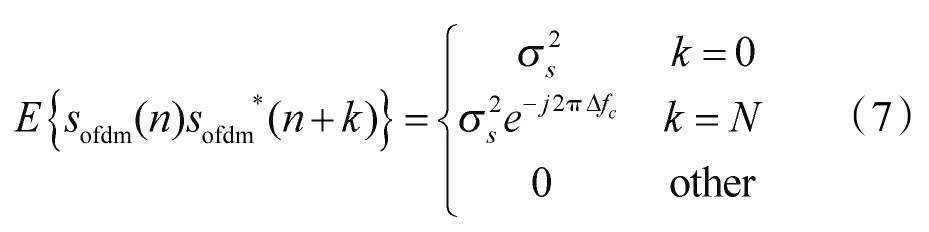
通过式（8）可知在k=Tu时，Rofdm（k）会出现第二个峰值。分析其原因是由于OFDM信号时域结构（如图1）特点所致。OFDM信号在结构上就具有自相关性，随着偏移长度k的变化，相关性结构也会发生变化，如图2所示。

图2 OFDM信号相关性结构图

两个信号相差Tu时，由于相关性公式，OFDM信号的循环前缀S1，S2，S3…会与本身相乘，从而出现了峰值，其所在点为Tu，而单载波信号由于没有相关性，所以不会存在波峰值。相比于文献［5］需要主观判定出现有规律的峰值来实现信号的盲检测，本算法实现更简单，且不需对循环前缀做预估计。

图3是OFDM信号和单载波信号的经过归一化处理的相关函数波形，可见OFDM信号在时延Tu处明显出现波峰，利用此分析结果不仅可以完成OFDM信号的有效盲识别，而且还可以估计出OFDM信号的有效长度T^'u。

图3 相关函数R（k）的波形

2.2 时域相关参数估计

在第2节中利用循环前缀的相关性，把相关函数|Rofdm（k）|的峰值中提取出的T^'u作为OFDM信号的有效长度，在此基础上完成对其它时域参数的估计。文献［5］提出对一个移动窗口内固定的相差T^'u个位置的接收数据求相关，采用OFDM信号的一次相关，且在估计值的基础上进行二次估计，增加了参数估计的误差，本文采用一个基于循环前缀相关的累加函数，对OFDM信号进行多次相关，弥补了二次估计误差大的不足，其定义为：

式（9）中表示采用A个OFDM信号的数据块，其中包括若干个OFDM信号的符号数。采用数据块的好处，是使得每隔Tx段数据有前I与I+'u之间相关性的累积和，I的取值最好应包括循环前缀的长度，即使比循环前缀长度短时，仍然可以利用循环前缀的前I个数据完成累积和识别，在仿真实验3，本文对I的取值进行仿真分析，Tx的取值应至少包含一个符号周期，由于此时并不知循环长度的值，根据已有的OFDM系统对保护间隔的要求，保护间隔不得低于符号总长度的1/16，在此取I='u/2，'u＜Tx＜2'u。A的取值要根据OFDM信号的实际长度，理论上I和A的值越大，OFDM信号累加的次数和长度越大，结果也就越准确，当然相应的运算量也会越复杂。因此，在实际应用中一般根据所需的精度取值。通过对图2的分析，可以发现只有当Tx=T时，即Tx的取值为OFDM信号的周期时，才能保证此时循环前缀中的I个值r（i=a+Tx）和r（i+aTx+'u）具有相关性，在的函数图中才会出现较大的峰值，如图4所示。

图4 时域参数的估计

2.3 算法步骤

在非协作通信领域，信号的调制方式及相关参数均是未知的，一般只能对接收到的一组数据进行处理，完成对OFDM信号的识别相关时域参数的检测。文献［5］需要预先设定循环前缀的长度TCP为符号长度T的1/4，使其适用性普遍性较差，并且符号长度T也要在几个常用的系统空间进行搜索，具有很大的局限性。文献［11］通过构造代价函数，从而引入了表示所选循环频率个数的参量Nb，增加了算法的复杂度，而且是在已知OFDM信号的基础上完成对时域参数的估计。本文依据OFDM信号的循环前缀的具有相关性，其相关值在相差Tu的距离会出现峰值，而单载波则不具备相关性，以此实现OFDM信号的盲识别并估计出OFDM信号的有效长度'u，然后在此基础上由定义的式（9），通过利用多个循环前缀的累积和找到最大值所在点估计出OFDM信号的的实际长度'，而循环前缀的长度'CP='-'u，最终完成对OFDM信号时域参数的估计，具体步骤如下：

3 实验仿真结果

利用计算机在MATLAB软件平台上完成对算法性能有效性的评估，仿真中OFDM系统的仿真参数：调制方式为16QAM，子载波数为128，单个OFDM信号的周期长度包括有用符号数Tu为512和循环前缀Tcp为128，4倍的过采样率，升余弦脉冲成型，采用多径信道（本仿真中采用3径信道）。单载波系统的仿真参数：调制方式为16QAM。

实验1：对OFDM信号和单载波信号的盲检测。

图5 信号检测率

用本文的算法步骤进行100次蒙特卡洛仿真，信噪比在-10 dB～5 dB的范围内，完成图5的信号检测图，通过图5可以看出在信噪比大于-5 dB时已经达到95%的识别率，表明本文算法在低信噪比情况下能够有效的区分OFDM信号和单载波信号，具有较好的识别效果。

实验2：对仿真中的OFDM的系统进行时域参数估计。

在相同条件下本文算法与文献［10］中的算法作对比，信噪比在-7 dB～5 dB的范围内，I的取值为256，以所求的OFDM信号周期长度与实际长度640的平均误差点数为纵坐标，取步长为1 dB的每个信噪比点做蒙特卡洛仿真求平均，如图6所示，在低信噪比条件下，本文的平均误差点数小于文献［10］的估计算法，并且受噪声影响较小，具有较高的识别效果。

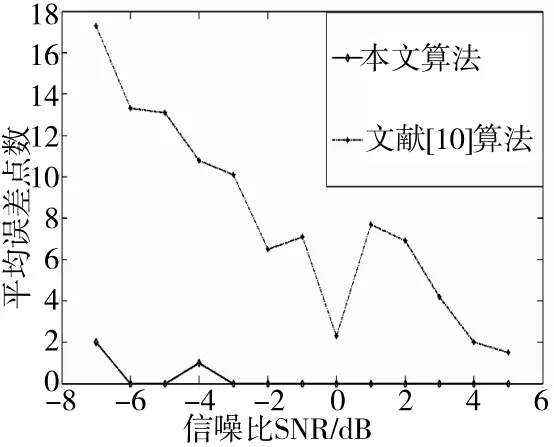
图6 OFDM信号周期长度的平均误差点数与信噪比的关系

实验3：对式（7）中不同的取值进行仿真分析。

在此把I的值分别取512，256，128，64，在不同的信噪比下进行蒙特卡洛仿真，针对性能评价，文献［11］定义估计误差小于精确值的1%，算法就能识别各系统，对于实际符号长度为640的OFDM信号的平均估计偏差点数在6个数据点内，图5中基本满足正确估计的要求，并且随I值的增大效果越来越好，但同时相应的运算量也在增大，所以在进行时域参数估计时可根据所需要的精度，对I的值进行实时选择。本实验有效地证明不需要对循环前缀的长度进行预估计来实现OFDM信号时域参数的识别，克服了文献［5］中必须预先假设循环前缀长度的局限性，具有更高的普遍实用性。

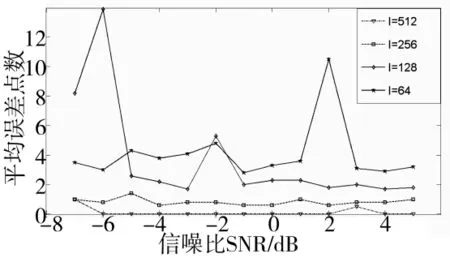
图7 不同I长度下的平均误差点数

4 结论

本文对OFDM信号的特点进行分析，根据对其循环前缀与其末尾数据的相关性原理，通过自相关函数在偏移有效长度时产生的极大值，完成对OFDM信号的盲识别，并在极大值处估计出OFDM信号的有效长度，再根据多个循环前缀相关性累加和的极大值找到OFDM信号的符号长度，从而完成对OFDM信号时域参数的估计。算法步骤简单，并且不需要进行载波估计、波形估计和循环前缀估计等预处理，以及信号调制样式，信道噪声等先验知识，具有较好的盲识别和参数估计效果。仿真实验表明，该方法在信噪比较低的情况下具有较高的实用价值和现实意义。

［1］佟学俭，罗涛.OFDM移动通信技术原理与应用［M］，北京：人民邮电出版社，2003.

［2］Akmouche W．Detection of Multicarrier Modulations Using 4th-order Cumulants［C］//IEEE Military Communications Conference，Atlantic，USA，1999.

［3］吕挺岑，李兵兵，董刚.一种多径信道下的OFDM信号盲识别算法［J］.现代电子技术，2007（11）：13-16.

［4］黄奇珊，彭启琮，路友荣，等.OFDM信号循环谱结构分析［J］.电子与信息学报，2008，30（1）：134-138.

［5］曹鹏，彭华，董延坤，等.一种基于循环前缀的OFDM盲检测及参数估计算法［J］.信息工程大学学报，2010，11（2）：196-200.

［6］张路平，王建新，马宁.多径信道下OFDM信号和单载波信号的盲识别［J］.宇航学报，2012，33（9）：1289-1294.

［7］Yong S C，Jaekwon K著，孙锴，黄威译．MIMO-OFDM无线通信技术及MATLAB实现［M］.北京：电子工业出版社，2013.

［8］张天骐，王玉娥，包锐，等.多径衰落信道下OFDM信号盲识别［J］.北京邮电大学学报，2012，35（6）：74-78.

［9］Dobre O A，Punchihewa A，Rajan S，eta1．On the Cyclostatianafity of OFDM and Single Carrier Linearly Digitally Modulated Signals in Time Dispersive Channels with Applications to Modulation Recognition［C］//IEEE Wireless Communications and Networking Conference，Las Vegas，USA，3，2008.

［10］王雪.OFDM信号检测与调制识别［D］.合肥：中国科学技术大学，2009.

［11］蒋清平，杨士中，张天骐，等.时变衰落信道下OFDM信号参数融合估计［J］.系统工程与电子技术，2011，33（7）：1627-1632.

Blind Recognition and Parameter Estimation for OFDM Signals Based on Correlation

ZHANG Meng-bo1，YANG Xiao-jing1，ZHANG Xin-ran2，FAN Bin-bin1
（1.Electronic Engineering Institute of PLA，Hefei 230037，China；
2.Anhui University，Hefei 230039，China）

An algorithm for blind recognition and parameter estimation based on cyclic prefix correlation is proposed to solve the problem of recognition of OFDM signal in non-cooperative communication.Through analysising the cyclic autocorrelation function of OFDM signal and calculating delay autocorrelation function of the waveform in the time domain，blind recognition of OFDM signals and single carrier signal is realized.On this basis，the accumulation function based on cyclic prefix correlation is formed by using a plurality of OFDM signals.Then，through the utilization of the peak of waveform constructed by the accumulation function，the parameter estimation of symbol and the length of cyclic prefix is realized.

OFDM，cyclic prefix，correlation function，blind recognition，parameter estimation

TN911

A

1002-0640（2015）05-0099-05

2014-03-05

2014-05-22

张孟伯（1990- ），男，安徽宿州人，硕士研究生。研究方向：通信信号处理。