导弹舵机MIT-Lyapunov复合控制研究*

何素娟，张云燕，曹立学

（1.陕西理工学院电气学院，陕西 汉中 723000；2.西北工业大学航天学院，西安 710072）

导弹舵机MIT-Lyapunov复合控制研究*

何素娟1，张云燕2，曹立学1

（1.陕西理工学院电气学院，陕西 汉中 723000；2.西北工业大学航天学院，西安 710072）

建立了导弹舵机系统的数学模型，提出了模糊自适应控制分配与复合控制器设计方案，使采用MIT-Lyapunov复合控制方法设计的控制器能够克服导弹舵机系统在导弹飞行范围发生大的变化时，舵机参数剧烈变化带来的影响。最后利用Matlab/Simulink对舵机系统进行了仿真分析。仿真结果表明：该控制器能够解决舵机在参数发生变化后控制效果变差的问题，使舵机系统具有较好的稳定性和快速响应性。

导弹舵机，自适应控制，复合控制

0 引言

文献［1］提出的基于PID和自适应控制相结合的复合控制方法，及文献［2］提出的基于波波夫超稳定理论的自适应控制方法，解决了控制对象的参数发生变化后控制效果变差的问题，但都没有涉及跟踪误差的收敛速度和稳定性之间的矛盾。本文提出了一种基于MIT-Lyapunov的复合控制方法，充分利用MIT算法的收敛速率与误差大小成正比的特点，采用模糊自适应分配方法，在误差较大时使用MIT算法，使误差快速收敛；当误差较小时，使用Lyapunov方法，使系统快速稳定。仿真结果表明，采用这种方法设计的控制器有效地提高了系统的稳态精度和动态品质，具有很强的鲁棒性。

1 舵机系统的数学模型

典型导弹舵机系统的组成结构如图l所示。

图1 舵机组成结构图

电动舵机的运动方程可以用下面的几个方程来描述［1-2，5-6］：

电枢回路电压平衡方程：

电磁转矩方程：

电动机轴上的转矩平衡方程：

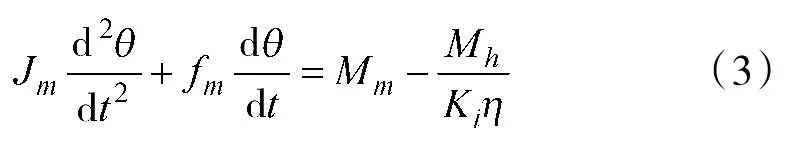
设δ为舵轴转角，它与电机转角θ的关系为：

式中：ia为电枢中的电流；Ra为电枢电阻；La为电枢电感；Jm为电动机和负载折合到电机轴上的转动惯量；Mm为电机在电流作用下产生的电磁转矩，Mh为舵机的铰链力矩；Ce为反电动势系数；Cm为转矩系数；Ki为传动比；η为传动效率。由式（1）～式（3）可得：

由于电枢电路电感La较小，通常忽略不计。根据直流伺服电机运动方程，由式（1）～式（5）可得出控制电压ua到舵偏角δ的传递函数为：

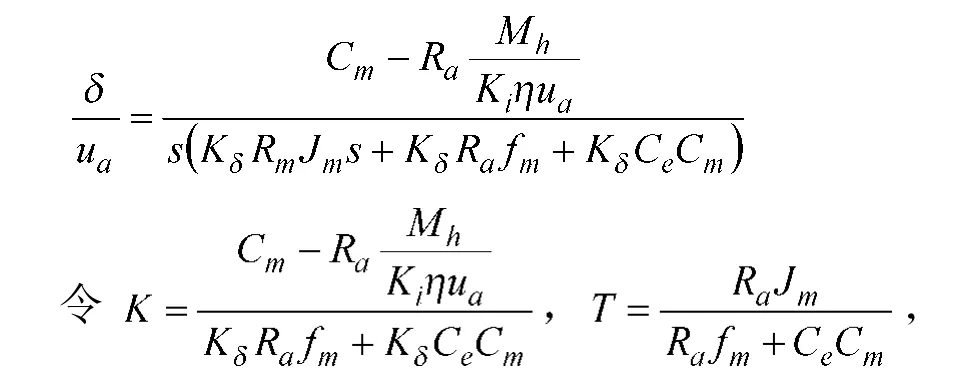
则上式可以写成

由式（6）可以看出，典型的电动舵机系统可以简化为一个二阶时变系统，参数K的大小与电动舵机的铰链力矩Mh和伺服电机的控制电压ua有关。由文献［8］可知：

式中，mh为铰链力矩系数，随导弹飞行速度和飞行高度的变化而变化；qt为流经操纵面的动压；St为舵面面积；bt为舵面弦长。此外，伺服电机的输入电压ua由要求的舵偏角和实际舵偏角的偏差来确定，也是时变的。因此，由式（6）所定义的电动舵机系统传递函数是时变的，且变化范围很大。这就给舵机控制器的设计提出了更高的要求。

2 控制器设计

由式（6）可以看出，电动舵机系统的传递函数不满足正实性条件，不能直接设计MIT自适应控制器。因此，可以在舵机系统后串联一个微分补偿器，使系统变为最小相位系统。为了保证舵机系统模型的不变性，可以在系统后再串联一个积分补偿器［1］。假设变成最小相位系统后的被控对象模型为：

参考模型的传递函数为：

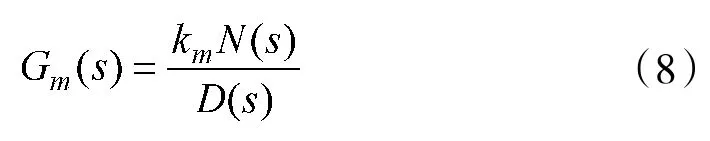
系统的方框图如图2所示。图中的自适应机构根据ε的大小来调整kc，使得ε（t）→0，控制对象的输出yp趋近于参考模型的输出ym。

图2 自适应系统方框图

被控对象的传递函数与参考模型的传递函数基本部分是相同的，参考模型的增益km是常值，被控对象的增益kp随着外界环境或其他干扰的变化而变化。利用自适应机构来调整kc的值，使得kckp与参考模型增益km一致。

根据文献［9］可以得到可调增益的调节规律，即系统的自适应规律

式中，μ=λkp/km为一常数。

3 模糊自适应控制分配方法

模型参考设计的目的就是使舵系统的输出δ能够快速、稳定地跟踪输入指令δc。采用模型参考自适应控制的分配方法，如图2所示，MIT算法根据跟踪误差ε（t）的大小来调整kc，使得ε（t）→0，控制对象的输出yp趋近于参考模型的输出ym。

由于MIT算法的收敛速率与跟踪误差ε（t）大小成正比，当ε（t）比较大时，MIT方法能够使误差快速收敛，但是当ε（t）较小时，收敛性能较差。因此，当ε（t）较小时，采用Lyapunov方法来改进MIT算法的收敛性。Lyapunov算法规则如下［3-4］：

对式（11）求导得：

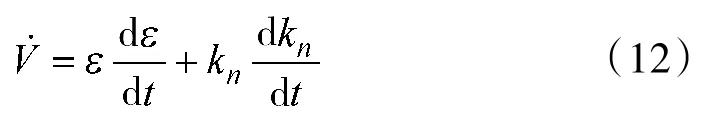
由于MIT算法在误差ε（t）较大时收敛较快，但不能保证稳定性，而Lyapunov算法则正好相反，因此，可以通过MIT和Lyapunov两种算法的结合来保证跟踪误差快速、稳定的趋近于零。由模糊推理系统自动选择两种算法输出的权重，分配策略如图3所示。

图3 模糊自适应分配算法结构图

将误差ε（t）分为3个模糊集合：大（L）、零（Z）、小（S），将两种自适应算法的权重q1，q2分为3个模糊集合：小（S）、零（Z）、大（L），模糊规则如表1所示［3，10］。

表1 模糊控制规则表

4 仿真与分析

为了验证控制算法的有效性，本文以文献［1-2］中的某型导弹舵机为例，对本文设计的MIT-Lyapunov复合控制器进行仿真。舵机的具体参数为：

选取参考模型为空载时的舵机模型。经计算，参考模型的传递函数为：

被控对象的传递函数为：

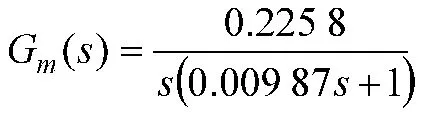
根据舵机系统性能指标要求，采用单位阶跃信号，使用MIT-Lyapunov复合控制方法，并利用Matlab/Simulink进行仿真。仿真结果如下：

图4 输出响应曲线

图5 拉偏10%后的输出响应曲线

图4 为采用PID控制和采用复合控制的舵机输出响应曲线；图5为舵机参数拉偏10%后采用PID控制和采用复合控制的舵机输出响应曲线。

PID控制器与复合控制器控制效果比较结果，如表2所示。

表2 PID控制器与复合控制器控制效果比较

从表2的数据对比可以看出，当舵机参数发生剧烈变化时，传统的PID控制方法不能满足系统的快速性要求，而采用模糊自适应分配的复合控制方法能够有效地克服参数变化的影响，控制效果能够满足系统的要求［14］。

5 结论

基于电动舵机的数学模型，本文采用模糊推理分配策略和MIT-Lyapunov复合控制方法设计了自适应控制器，利用Matlab/Simulink对导弹的舵机系统的仿真结果表明：在导弹的飞行状态发生剧烈变化时，用该方法设计的控制器能够保证舵机响应的快速性和稳定性，具有较强的鲁棒性。

［1］高原，谷良贤.导弹舵机PID-MRAC复合控制仿真研究［J］.计算机仿真，2008，28（1）：66-69.

［2］朱宇光，曹彪，汪浩.基于超稳定理论的导弹电动舵机自适应控制方法研究［J］.机电工程，2012，29（6）：693-695.［3］周锐，王军.导弹气动力/直接力自适应控制分配及优化设计［J］.航空学报，2007，28（1）：187-190.

［4］刘皓，沈毅.敏捷导弹复合控制策略［J］.系统工程与电子技术，2011，33（1）：874-878.

［5］Yang B Q，Bi Y T，Yao Y，et al.Blended Control with Lateral Thrust and Aerodynamic Force Based on Predictive Control［J］.Chinese Control Conference，2010:6161-6166.

［6］Yong S C，Choi C L，Jae W C.Autopilot Design for Agile Missile with Aerodynamic Fin and Side Thruster［C］//SICE AnnualConference.Japan，Fukui:IEEC Press，2003: 1476-1481.

［7］Menon P K，Iragavarapu V R.Adaptive Techniques for Multiple Actuator Blending［R］.AIAA 98-4494，1998.

［8］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2006.

［9］李言俊，张科.自适应控制理论及应用［M］.西安：西北工业大学出版社，2005.

［10］席爱民.模糊控制技术［M］.西安：西安电子科技大学出版社，2008.

［11］彭书华，李华德，苏中，等.不确定参数电动舵机滑模变结构控制［J］.电机与控制学报，2009，13（1）：128-132.

［12］杨栓虎.高精度宽频带电动比例舵机技术研究［D］.北京：北京理工大学，2000.

［13］杨海容.基于变结构控制的电动舵机设计［D］.上海：上海交通大学，2012.

［14］吕飞.舵机反操纵对于自动驾驶仪稳定性的影响［J］.四川兵工学报，2013（9）：8-10.

Research on MIT-Lyapunov Blended Control of Missile Electric Servo Actuator

HE Su-juan1，ZHANG Yun-yan2，CAO Li-xue1
（1.School of Electrical Engineering，Shaanxi University of Technology，Hanzhong 723000，China；
2.College of Astronautics，Northwestern Polytechnical University，Xi’an 710072，China）

The model of the actuator system is established.The design scheme fuzzy adaptive control allocation with blended controller is proposed.To overcome the effect caused by the parameter change of the actuator system while the missile flight range is large，the controller is designed based on the compound method of MIT-Lyapunov.At last，analysis and simulation of actuator system was completed using Matlab/Simulink.The results indicate that the adaptive controller can solve the problem of bad effect caused by the actuator’s parameter fierce change，and can make the actuator system response the command stably and quickly.

missile actuator，adaptive control，blended control

TP273

A

1002-0640（2015）05-0005-03

2014-02-23

2014-04-17

陕西省教育厅基金项目（11JK0934）；博士启动基金资助项目（SLGQD13（2）-6）

何素娟（1979- ），女，河北新乐人，讲师，博士。研究方向：飞行器制导与控制，先进控制理论及其应用。