整车物流配送优化模型及算法实现

胡文耀

（南京财经大学，江苏 南京 210023）

工程科技

整车物流配送优化模型及算法实现

胡文耀

（南京财经大学，江苏 南京 210023）

整车物流指的是按照客户订单对整车快速配送的全过程。随着我国汽车工业的高速发展，整车物流量，特别是乘用车的整车物流量迅速增长。在确保完成运输任务的前提下，物流公司追求降低运输成本。文章针对整车物流，在控制运输成本最小化的前提下，结合实际的案例，分别讨论了无路径和含路径问题，进行分析并建立相应的模型，最后得出优化的运输方案。

整车物流;优化模型;装载方案

一、引言

整车物流是基于时间竞争的敏捷汽车供应链环境中，以整车作为物流服务标的物，按照客户订单对交货期、交货地点、品质保证等的要求进行快速响应和准时配送。整车物流从简单的商品车运输变化为以运输为主体，仓储、配送、末端增值服务为辅的新型物流。中国整车物流行业起始于20世纪90年代，是伴随着中国汽车产业逐步发展而发展的，并密切跟随中国汽车产业的发展经历了从无到有、从粗浅到专业、从被动仿效到主动创新的逐步发展提升。

“十二五”是我国加快转变经济发展方式的关键时期，汽车产业是我国的支柱产业，将成为转变发展方式的领跑者。工信部统计数据显示，2014年中国汽车产销分别为2372万辆和2349万辆，同比增长7.3%和6.9%，汽车产销量双双突破2300万辆。自2009年起，连续六年排名全球第一。汽车物流作为汽车产业发展的重要支撑条件之一，不仅做好产业的基础保障，也将成为汽车产业转变经济发展方式的重要引擎。汽车物流行业将通过组织创新、市场创新、技术创新、服务创新，提高物流服务的附加值，继续向汽车产业供应链全过程渗透和融合，为优化汽车产业结构、节约汽车产业成本、提高产业运行效率和效益，发挥重要的促进和带动作用。

二、问题的分析

整车物流指的是按照客户订单对整车快速配送的全过程。随着我国汽车工业的高速发展，整车物流量，特别是乘用车的整车物流量迅速增长。图1、2、3就是乘用车整车物流实施过程中的画面。

图3 2-2型轿运车

乘用车生产厂家根据全国客户的购车订单，向物流公司下达运输乘用车到全国各地的任务，物流公司则根据下达的任务制定运输计划并配送这批乘用车。为此，物流公司首先要从他们当时可以调用的“轿运车”中选择出若干辆轿运车，进而给出其中每一辆轿运车上乘用车的装载方案和目的地，以保证运输任务的完成。“轿运车”是通过公路来运输乘用车整车的专用运输车，根据型号的不同有单层和双层两种类型，由于单层轿运车实际中很少使用,本文仅考虑双层轿运车。双层轿运车又分为三种子型：上下层各装载1列乘用车，故记为1-1型（图1）；下、上层分别装载1、2列，记为1-2型（图2）；上、下层各装载2列，记为2-2型（图3）。

在确保完成运输任务的前提下，物流公司追求降低运输成本。但由于轿运车、乘用车有多种规格等原因，当前很多物流公司在制定运输计划时主要依赖调度人员的经验，在面对复杂的运输任务时，往往效率低下，而且运输成本不尽理想。

三、假设及符号说明

本文对装载具体假设如下：每种轿运车上、下层装载区域均可等价看成长方形，各列乘用车均纵向摆放，相邻乘用车之间纵向及横向的安全车距均至少为0.1米，下层力争装满，上层两列力求对称，以保证轿运车行驶平稳。受层高限制，高度超过1.7米的乘用车只能装在1-1型、1-2型下层。其中，轿运车、乘用车规格如下：

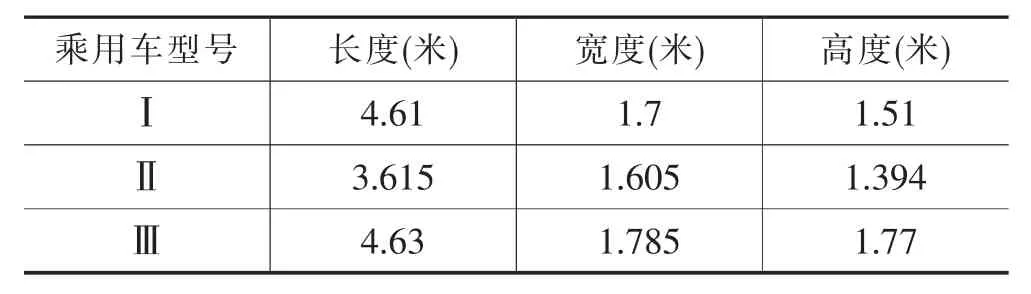
表1 乘用车规格

表2 轿运车规格

整车物流的运输成本计算较为繁杂,这里简化为：影响成本高低的首先是轿运车使用数量；其次，在轿运车使用数量相同情况下，1-1型轿运车的使用成本较低，2-2型较高，1-2型略低于前两者的平均值，故本文在下述模型中不再考虑2-2型轿运车，且物流公司1-2型轿运车拥有量小，为方便后续任务安排，每次1-2型轿运车使用量不超过1-1型轿运车使用量的20%；再次，在轿运车使用数量及型号均相同情况下，行驶里程短的成本低，注意因为该物流公司是全国性公司，在各地均会有整车物流业务，所以轿运车到达目的地后原地待命，无须放空返回。最后每次卸车成本几乎可以忽略。

i=1，2，3L，m；m表示安排1-1型轿运车的方案数；

j=1，2，3L，n；n表示安排1-2型轿运车的方案数；

aij:第i种方案中每辆1-1型轿运车承载的j型乘运车的数量；

bij:第i种方案中每辆1-2型轿运车承载的j型乘运车的数量；

xi:第i种方案中所使用的1-1型轿运车的数目；

yi:第j种方案中所使用的1-2型轿运车的数目；

p1p2:使用每辆第1-1型，1-2型轿运车的成本；

四、无路径问题

针对无路径情况，我们研究的问题是：假设物流公司要运输Ⅰ车型的乘用车156辆、Ⅱ车型的乘用车102辆及Ⅲ车型的乘用车39辆。

对于此问题，我们分两步解决。第一步先求得每类轿运车的运输方案，然后第二步，根据成本最小化，建立模型，求得最优运输方案。

第一步：根据整数规划中的分支与界限法，结合表1与表2中的数据，运用Matlab软件实现，求得1-1型和1-2型车上（下）层的可行装载方案。具体方案如表3，表4所示，其中An，Bn，Cn，Dn分别表示1-1型和1-2型轿运车上（下）层的装载方案。

表3.1 1-1型车上层装载方案

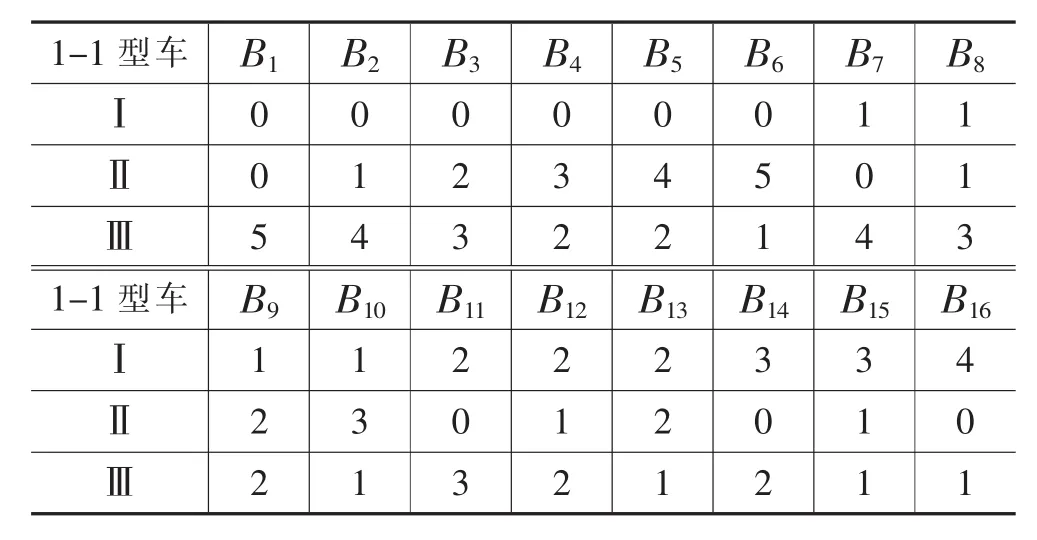
表3.2 1-1型下层装载方案

表4.1 1-2型上层装载方案

表4.2 1-2型下层装载方案

根据上表可得各类轿运车每层的装载方案，又上下层的方案相互独立。所以根据排列组合可知：对1-1型轿运车，装载Ⅰ、Ⅱ、Ⅲ型乘用车的可行方案共有5*16=80种；对1-2型轿运车，装载Ⅰ、Ⅱ、Ⅲ型乘用车的可行方案共有6*24=144种。其中，1-1型车和1-2型车的全车运输方案由于篇幅所限，不再列出。

第二步：建立模型

目标函数：

约束条件：

其中，目标函数表示运输成本的最小化，p1，p2分别表示租用每辆1-1型和1-2型轿运车的成本。在这里，为求得最优运输方案，我们不妨设p2=1.5p1，令p1=1。即每辆1-2型轿运车的成本是1-1型轿运车的1.5倍。

在约束条件中，第一个不等式表示1-2型轿运车使用量不超过1-1型轿运车使用量的20%；后面三个不等式分别表示运输Ⅰ、Ⅱ、Ⅲ车型的乘用车不少于上述问题中提出的156辆、102和39辆。

该模型运用lingo软件，进行编程、运行，最后得到最优解。整理结果，得到最优装载方案（见表5）。

表5 问题三的具体装配方案

五、含路径问题

针对含路径情况，我们研究的问题是：物流公司要运输166辆Ⅰ车型的乘用车（其中目的地A、B、C、D分别为42、50、33、41辆）和78辆Ⅱ车型的乘用车（其中目的地A、C分别为31、47辆）。具体路线见图4，各段长度：OD=160，DC=76，DA=200，DB=120，BE= 104，AE=60。

图4 路线示意图

对含有路径问题的物流方案，除考虑轿运车的型号及数量，还要考虑运输距离对成本的影响。我们采用逐点运输的思想。首先从O地到D地我们按各地总需求量进行装车，找出一个最优方案；到达D地后将D处所需的乘用车卸载，然后按C、B两地所需求的乘用车数量再次运输，找出一个从D到C的最优方案；再依次从D地到B地，再到A地，分别找出最优方案。最后把各地方案进行整合得到整体最优方案。

第一步：根据整数规划中的分支与界限法，结合表1与表2中的数据，运用Matlab软件实现，求得1-1型和1-2型车上（下）层的可行装载方案。具体方案如表6，表7所示，其中En，Fn，Gn分别表示1-1型和1-2型轿运车上（下）层的装载方案。

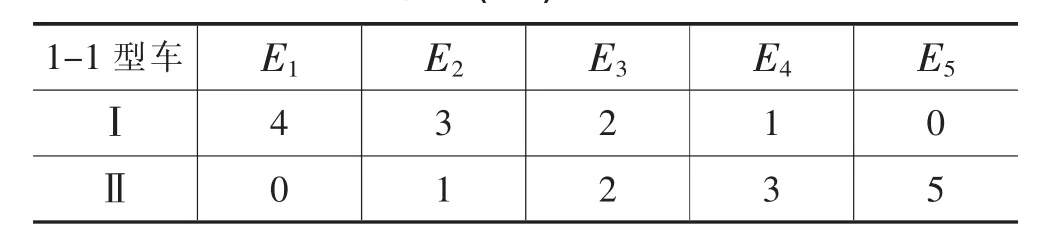
表6 1-1型车上（下）层的运输分配方案

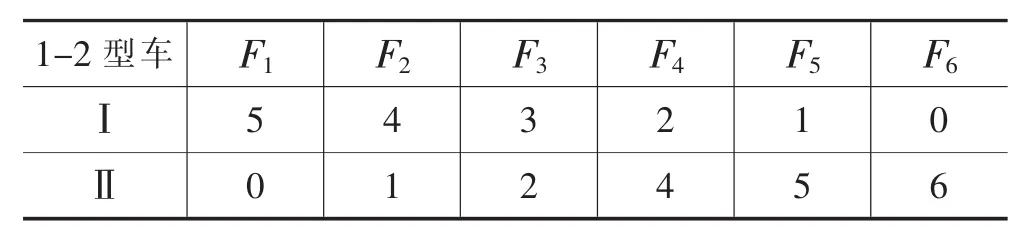
表7.1 1-2型车下层的运输分配方案

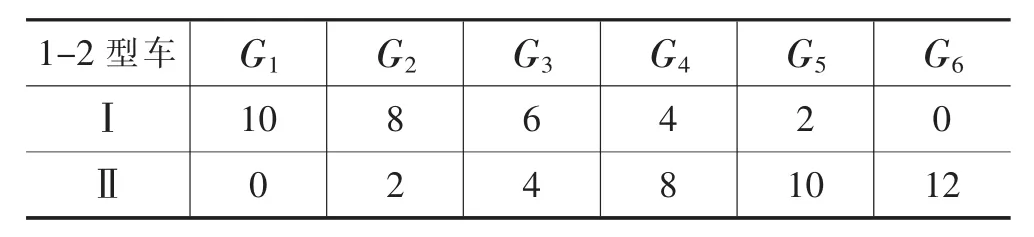
表7.2 1-2型车上层的运输分配方案

根据上表可得各类轿运车每层的装载方案，又上下层的方案相互独立。所以根据排列组合可知：对1-1型轿运车，装载Ⅰ、Ⅱ、Ⅲ型乘用车的可行方案共有5*5=25种；对1-2型轿运车，装载Ⅰ、Ⅱ、Ⅲ型乘用车的可行方案共有6*6=36种。其中，1-1型车和1-2型车的全车运输方案由于篇幅所限，不再列出。

第二步：建立模型

在问题二中，增添了路径这一限制条件，问题中假设所有的乘运车都从O地出发，分别送达各个目的地，在此过程中所有的路程均是有向路径。其中ct为到达第t段的距离。其中t=1表示O→D,t=2表示D→C，t=3表示D→B，t=4表示B→A。所以，c1=100；c2=76；c3=120；c4=80。xit表示第i种方案中运往t地所使用的1-1型轿运车的数目，yjt表示第i种方案中运往t地所使用的1-2型轿运车的数目，其中t=1,2,3,4。

以下是对约束条件的分析：

(1)使用1-2型轿运车的总量小于1-1型轿运车总量的20%

(2)首先把所有需要的Ⅰ、Ⅱ型乘用车166辆和78辆都先送到D点，为

得到最优装载方案为：

表11 问题二的D地装配方案

(3)由D地运送到C目的地的乘用车模型为：

得到最优装载方案为：

表12 问题二的C地装配方案

(4)由D地运送到B地的乘用车模型为：

得到最优装载方案为：

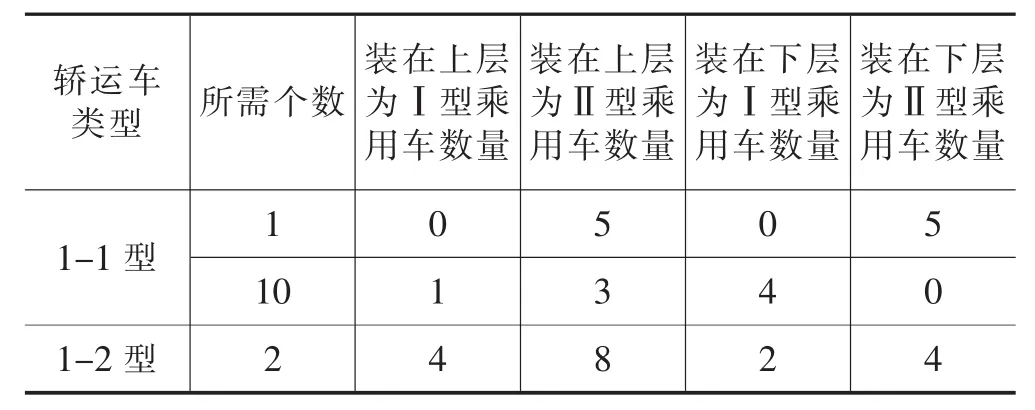
表13 问题二的B地装配方案

(6)由B地到达目的地A所需要的所有Ⅱ型车和Ⅰ型车的数量：

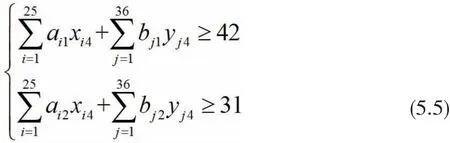
得到最优装载方案为：

表14 问题二的A地装配方案

目标函数：

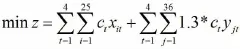
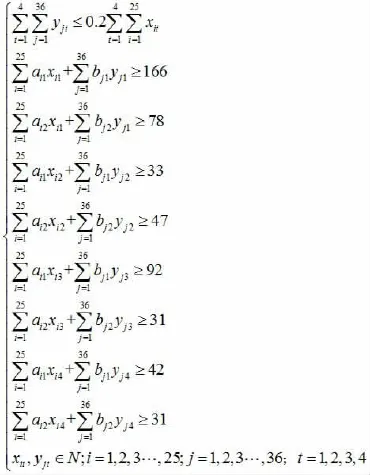
约束条件：最后得到总的运输方案为：

表15 问题二的总装配方案

六、总结

本文针对整车物流的装载与运输问题，分为无路径和含路径情况。在控制成本最小化的前提下，根据具体的案例，分别建立配送模型，应用MATLAB和Lingo软件进行编程及求解，得出优化的运输方案。方案的优化节省了里程,降低了运输成本,提高了整车物流的运送效率。算法与模型的结合，对解决物流问题有着决定性的作用。

[1]杨浩.模型与算法[M].北京：北方交通大学出版社，2002.

[2]陈光亭，裘哲勇.数学建模[M].北京:高等教育出版社，2010.

[3]越民义.组合优化导论[M].杭州:浙江科学技术出版社,2000.

[4]田元新，陈超，邹小勇，邱建丁.整车物流网络规划集成优化模型研究[J].计算机集成制造系统 ，2006，（63）：365.376.

[5]张立昂.计算机和难解性-NP完全性理论导论[M].北京:科学出版社,1990.

The Vehicle Logistics Distribution Optimization Model and Algorithm Implementation

Hu Wen－yao
（Nanjing University of Finance and Economics，Nanjing Jiangsu 210046,China）

Vehicle logistics refers to the process of according to customer orders for the fast delivery of the whole vehicle.With the rapid development of automobile industry of China,the number of vehicle logistics grows rapidly，especially the passenger car.In the premise to ensure the completion of transport task,the logistics companies pursuit the reduction the cost of transportation.Combined with actual case,the paper focus on vehicle logistics,under the premise of controlling the minimization the transportation cost,respectively discusses the situation of no path and containing the path.According to analysis,establish the corresponding model.At last,we obtained the terminal transportation of optimization scheme.

vehicle logistics;optimization model;loading plan

TP393；F252.2

A

1672-0547（2015）03-0103-05

2015-04-11

胡文耀（1989-），男，山东临沂人，南京财经大学应用数学学院硕士研究生，研究方向：数理统计。