基于Newton-Raphson法的孤岛微网三相潮流计算

王晓虎，裴昌盛，汤向洋

(中国能源建设集团江苏省电力设计院有限公司，南京市211102)

基于Newton-Raphson法的孤岛微网三相潮流计算

王晓虎，裴昌盛，汤向洋

(中国能源建设集团江苏省电力设计院有限公司，南京市211102)

对于孤岛运行的微网而言，正确分析系统状态和分布式电源的工作方式非常关键，所以高效精确的潮流计算显得尤为重要。提出在分布式电源工作于下垂控制模式的情况下，基于Newton-Raphson法的孤岛微网三相潮流计算方法，并简化了潮流方程，提高了计算效率。在此基础上，还考虑了分布式电源无功越限问题。最后在25节点三相不平衡的微网算例中验证了本文方法的正确性，将其结果与牛顿信赖域法进行比较。最后指出，本文的潮流计算方法具有较高的精度和效率，可作为进一步研究的基础。

微网；分布式电源；下垂控制；孤岛运行；潮流计算；三相不平衡

0 引 言

随着近年来分布式电源(distributed generation，DG)的快速发展，如何将难以控制的DG接入电网一直是一个备受关注的问题。微电网作为一个将DG、储能装置、能量转换装置、相关负荷和监控、保护装置等汇集而成的小型发配电系统，完全具备依靠自身的控制及管理供能实现功率平衡控制、系统运行优化、故障检测与保护、电能质量治理等方面的能力，成为解决DG接入电网的一个有效方案[1-3]。不仅如此，微电网也是主动配电网的一种实现方式，是传统电网向智能电网过渡的一个体现。

微电网又称微网，是一个能够实现自我控制、保护和管理的自治系统。与传统配电网不同，微网既可以与外部电网并网运行，也可以孤立运行。当微网孤立于外部电网运行时，微网中的DG起到了重要的作用，此时微网中所有的负荷都由DG来承担，DG之间如何协调运行十分重要。文献[4-6]深入研究了孤岛模式下含DG的微网，但文献[4]和[5]都将孤岛微网当成传统的电网来处理，即选择一个大容量的DG作为松弛节点，其他DG作为PV或PQ节点来计算，但DG的容量普遍不大，作为松弛节点并不合理。

作为分析微网的有力工具，潮流计算显得尤为重要，其结果是许多深入研究的基础，有着无可替代的作用，而微网一般是三相不平衡的，三相潮流计算的结果更有价值。文献[6]和文献[7]的孤立微网潮流计算考虑了DG的下垂特性，但在三相不平衡时其DG下垂特性与实际情况不符，关于这点文献[8]进行了详细探讨。文献[9]考虑了文献[8]中DG的下垂特性，并用牛顿信赖域法(Newton trust region，NTR)求解三相潮流，结果令人满意。但是由于NTR法本身的缺陷，无法在计算的同时考虑DG的无功越限问题，需计算完成后比较，并再次计算直到所有DG都满足上限约束为止，效率并不高。

本文采用Newton-Raphson(以下记作NR)法来求解孤岛微网的三相潮流，做了一定的数学处理简化了计算过程，并考虑了DG的无功越限问题，很大程度地提高了计算效率。计算结果和NTR法的结果进行了比较。

1 孤岛微网的系统模型

1.1 线路模型

不平衡三相系统的线路阻抗模型可表示为

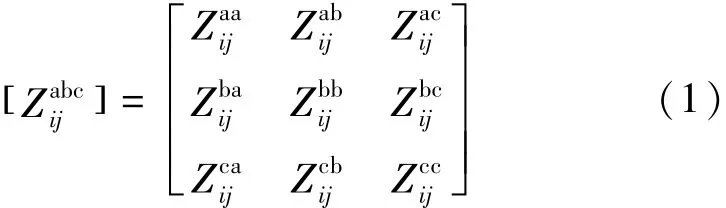
在运行于孤岛模式的微网中，系统频率不再是常量，而是一个变量，在计算系统的电抗时必须考虑系统频率的影响。即计算阻抗矩阵时不再是一个常数，其具体数值和系统频率有关。本文中为了使计算更简便高效，不失精度地忽略了频率对阻抗的影响。

1.2 负荷模型

在孤岛微网中，系统电压和频率对节点负荷的影响较大，使用常数不再适宜，为此采用静态负荷模型来计算负荷实际大小，从而考虑了电压和频率的影响。

幂函数型静态负荷模型的计算表达式如下:

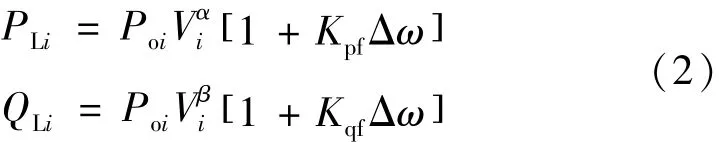
式中:PLi、QLi表示节点i的实际有功负荷和无功负荷；Poi、Qoi表示节点i的基准有功负荷和无功负荷；Vi表示节点i的电压；α和β分别为有功负荷和无功负荷的电压特性系数；Kpf、Kqf分别为有功负荷和无功负荷的频率特性系数；Δω＝ω-ω0为系统频率与基准频率的偏差。式(2)适用于各相负荷计算。

对于不同的负荷类型，频率特性系数和电压特性系数也不同，具体可参考文献[10]。

1.3 分布式电源DG模型

当微网和输电网互联时，DG的出力负荷较小，一般控制为PV或PQ节点进行处理。当微网运行于孤岛模式时，DG可以运行在3种模式:PV、PQ和下垂控制(droop control)模式。由于孤岛微网中不存在实际的松弛节点，DG不可能全部运行于PV和PQ这两种模式。

当DG运行于下垂控制模式时，其有功出力通过微网的系统频率来分配[8-9]:

式中:ω∗为基准功率设定值；mp为有功静态下垂增益系数；PG为DG的有功出力。值得注意的是，式(3)中PG为DG三相有功出力的总和，即DG的各相有功出力并不需要相等。

当DG运行于下垂控制模式时，其无功出力则通过DG的电压来控制:

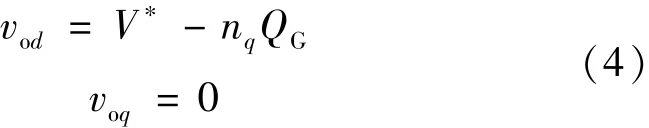
式中:vod和voq分别为DG电压的d轴和q轴分量；V∗为基准电压功率设定值；nq为无功静态下垂增益系数；QG为DG的三相无功出力总和。经Park变化后，式(4)可化为:

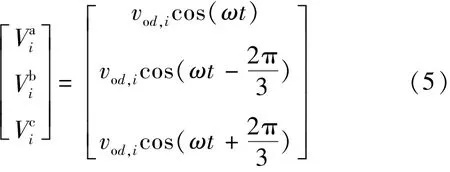
由式(5)可知，此时DG的三相电压的幅值是相等的。

DG的增益系数计算可参考文献[8-9]。

2 孤岛微网的三相潮流计算

2.1 潮流计算未知量

系统中每个PQ节点的未知量有6个，分别为三相电压Va、Vb、Vc和三相相角θa、θb、θc。系统中每个PV节点的未知量有3个，为三相相角θa、θb、θc。

系统中每个运行于下垂模式的DG节点的未知量有12个，为三相电压Va、Vb、Vc，三相相角θa、θb、θc，三相有功出力和三相无功出力

最后，还应包括系统的频率ω。

2.2 节点功率方程

节点i各相的注入有功和无功可表示为:

式中:m＝a，b，c；p＝a，b，c。

对于系统中每个处于下垂控制模式的DG节点，对应共有12个方程:

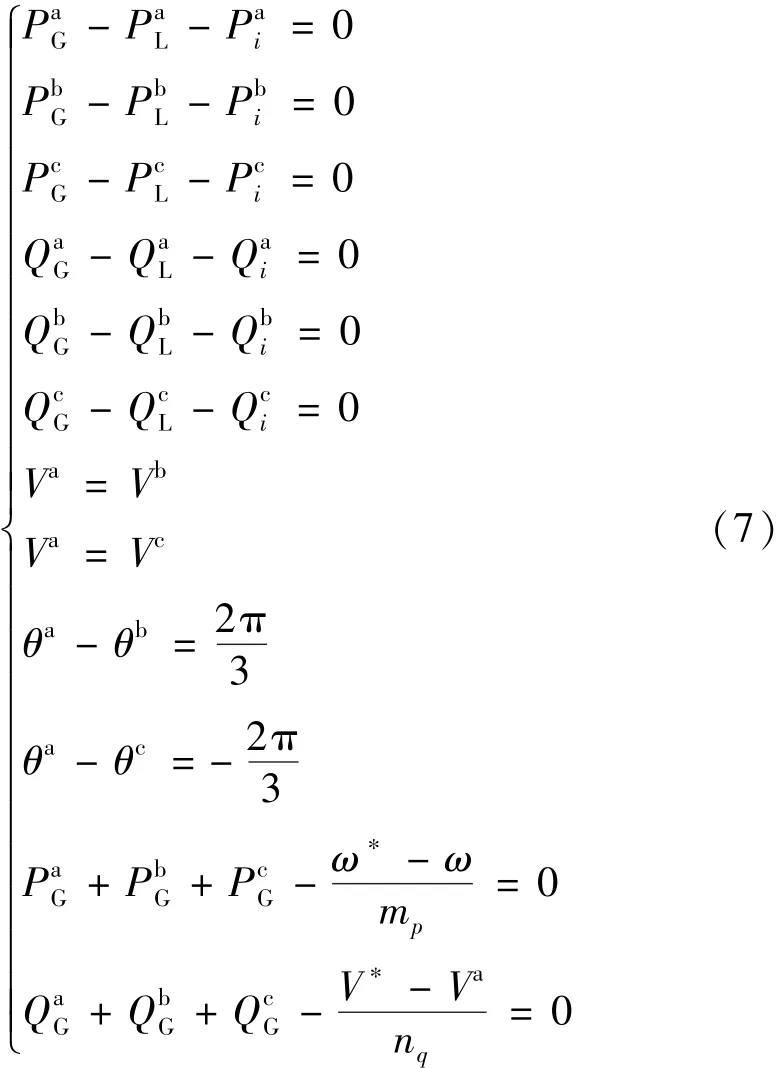
对于系统中每个PQ节点，对应共有6个方程:

对于系统中每个PV节点，对应共有3个方程:

最后还需要提供一个参考相角，令

由此可知，潮流计算的方程数与未知数相等，理论上可以使用Newton-Raphson法求解出结果。

2.3 改进后的节点功率方程

由2.1和2.2节给出的公式，不难发现下垂控制的DG节点所列方程非常多，是PQ节点方程数的2倍，在进行潮流计算时处理非常繁琐。

根据1.3中的结论可知，下垂控制的DG三相电压相等，相角对称，而三相总的出力有功和无功也和频率有关，因此可以根据这些特性对下垂控制的DG方程进行简化，简化后DG对应的变量为电压V，A相相角θ，A、B相有功出力和A、B相无功出力，简化后的方程如下:

式中所有的电压和相角都用A相电压V和A相相角θ来表示。这样，每个DG点的方程数便被缩减为6个。

2.4 NR法潮流计算

根据2.2、2.3中的节点功率方程，可列出修正方程为

式中:ΔW＝[ΔP1，ΔQ1，…，ΔPn，ΔQn]T为功率的偏差量；ΔX为状态量的修正量，其表达式为

式中，当节点i为非下垂控制DG点时:

当节点i为下垂控制的DG点时，

式(12)中J为雅科比矩阵，可根据ΔW和ΔX元素的求取，这里不再赘述。

2.5 DG节点控制模式的转化

DG一般都装有限流器以限制其无功不会无限地增大，本文亦考虑到这点，其转换模式如下:

(1)当下垂控制模式的DG出力无功达到其上限时(此时电压亦降至相应数值)，则将其无功出力限制于上限值，而电压则可在低于边界电压值的情况下变动；

(2)当处于无功上限模式的DG的电压值增大至边界电压时，DG再次进入下垂控制模式，此时电压应在高于边界电压值的情况下变动。

3 算例分析

本文使用的算例为25节点的三相不平衡测试系统[9]，并假设所有DG点运行于下垂控制模式。负荷的所有特性参数参考文献[10]，本算例中所有负荷的参数都设为夏季的民用负荷。本算例程序使用C语言编写，收敛精度为10-5。

算例中所有DG的参数如表1所示，表2和表3为计算结果，系统的最终频率为0.998 108。

从表2和表3可以看出，此时1号DG的无功出力均已达到上限；DG按比例分配系统的无功负荷；DG三相的出力有功功率和出力无功功率是不同的，但三相电压始终相同，三相相角也是始终对称的。

表1 DG参数Table 1 Parameters of DG

为了验证计算结果的正确性，将计算结果和NTR法的结果进行比较，其最大误差不超过10-3。造成误差的主要原因在于本文1.1节中线路模型所做的近似，频率变化一般不会超过1%，对线路模型不会造成太大影响，NR法足以保证计算精度。表4比较了2种方法之间的优劣。

从表4中可以看出，NTR法需要计算2次才能得到最终结果，其原因是NTR法无法在计算的同时考虑DG无功越限的问题，需要在得到计算结果并与设定参数比较后，修改程序再次计算才可得到最终结果。如果有多个DG达到无功出力上限，则需计算多次，其计算效率明显不如NR法。

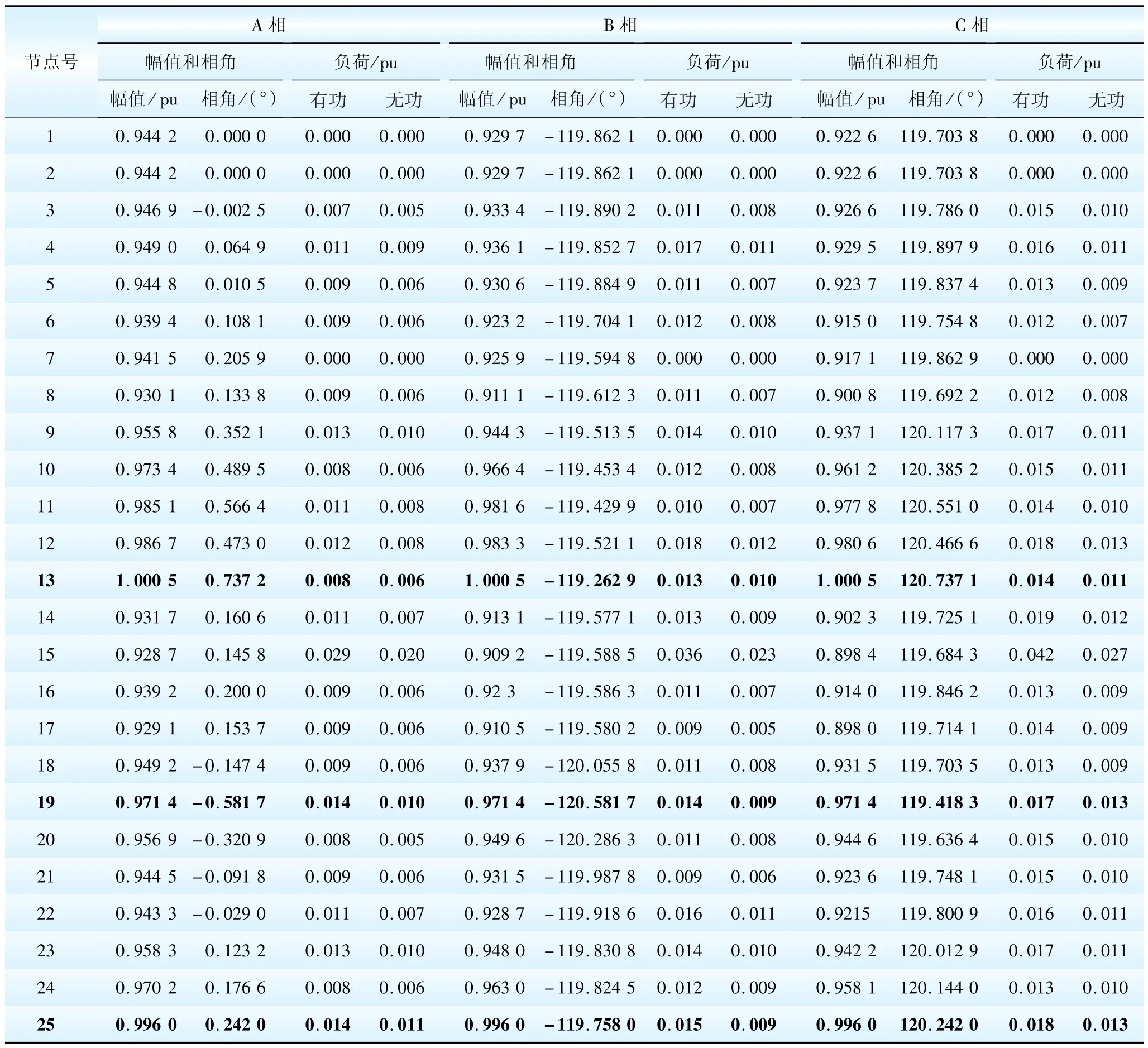
表2 NR法潮流计算结果Table 2 Power flow calculation results in NR Method

表3 DG的有功和无功出力Table 3 Active and reactive power output of DG

表4 NTR法和NR法的比较Table 4 Comparison between NTR method and NR method

4 结 论

本文采用NR法计算了孤立微网的三相不平衡潮流，并考虑了DG的下垂特性和DG的无功越限问题，计算结果精度令人满意，具有十分重要的研究价值。

但本文中考虑的DG下垂特性并不是唯一，其接口阻抗的性质不同也将导致下垂特性的不同，潮流的方程也得做出相应的改变，是否可以如此简化还亟待探讨，也值得进一步研究。

[1]李鹏，窦鹏冲，李雨薇，等.微电网技术在主动配电网中的应用[J].电力自动化设备，2015，35(4):8-16.

Li Peng，Dou Pengchong，Li Yuwei，et al.Application of microgird technology in active distribution network[J].Electric Power Automation Equipment，2015，35(4):8-16.

[2]鲁宗相，王彩霞，闵勇，等.微电网研究综述[J].电力系统自动化，2007，31(19):100-107.

Lu Zongxiang，Wang Caixia，Min Yong，et al.Overview on microgird research[J].Automation of Electric Power Systems，2007，31(19):100-107.

[3]郑漳华，艾芊.微电网的研究现状及在我国的应用前景[J].电网技术，2008，32(16):27-31.

Zheng Zhanghua，AiQian.Presentsituationofresearchon microgrid and its application prospects in China[J].Power System Technology，2008，32(16):27-31.

[4]Nikkhajoei H，Iravani R.Steady-state model and power flow analysis of electronically-coupled distribution resource units[J].IEEE Transactions on Power Delivery，2007，22(1):721-728.

[5]Kamh M Z，Iravani R.Unbalanced model and power-flow analysis of microgrids and active distribution systems[J].IEEE Transactions on Power Delivery，2010，25(4):2851-2858.

[6]刘杨华，吴政球.孤岛运行的微电网潮流计算方法研究[J].电力系统保护与控制，2010，38(23):16-20.

Liu Yanghua，Wu Zhengqiu.Study on power flow calculation method for islanding micro girds[J].Power S，stem Protection and Control，2010，38(23):16-20.

[7]刘杨华，吴政球，林舜江.孤岛运行的微电网三相不平衡潮流计算方法研究[J].湖南大学学报(自然科学版)，2009，36(7): 36-40.

LiuYanghua，WuZhengqiu，LinShunjiang.Researchon unbalanced three-phase power flow calculation method in Islanding micro grid.Journal of Hunan University(Natural Sciences)，2009，36(7):36-40.

[8]Yao W，Chen M，Guerrero J M，et al.Design and analysis of the droop control method for parallel inverters considering the impact of the compleximpedanceonthepowersharing[J].IEEE Transactions on Industrial Electronics，2011，58(2):576-588.

[9]Abdelaziz M M A，Farag H E，El-Saadany E F，et al.A novel and generalized three-phase power flow algorithm for islanded microgrids using a Newton trust region method[J].IEEE Transactions on Power Systems，2013，28(1):190-201.

[10]IEEETaskForceonLoadRepresentationforDynamic Performance.Bibliography on load models for power flow and dynamic performance simulation[J].IEEE Transactions on Power Systems，1995，10(1):523-538.

(编辑：刘文莹)

Three-Phase Power Flow Calculation for Isolated Island Microgrid Based on Newton-Raphson Method

WANG Xiaohu，PEI Changsheng，TANG Xiangyang
(Jiangsu Power Design Institute Co.，Ltd.of China Energy Engineering Group，Nanjing 211102，China)

The correct analysis of system state and the working mode of distributed generation are very important to the microgrid in isolated island operation，so a fast power flow calculation with high efficiency is very significant.Based on Newton-Raphson method，a three-phase power flow algorithm was proposed for isolated island microgrid with distributed generation operating in droop control mode，whose power flow equation was simplified and computational efficiency was improved.On this basis，the limit problem of reactive power of distributed generation was also considered.Finally，the correctness of proposed method was verified in a mircogrid test system with 25-bus three-phase unbalance，whose results were compared with Newton trust region method.The results indicate that the proposed power flow algorithm has high accuracy and efficiency，which can be used as the basis for further research.

microgrid；distributed generation；droop control；isolated island operation；power flow calculation；threephase unbalance

TM 74

A

1000-7229(2015)11-0130-05

10.3969/j.issn.1000-7229.2015.11.020

2015-05-29

2015-10-14

王晓虎(1980)，男，高级工程师，主要研究方向为电力系统自动化；

裴昌盛(1990)，男，助理工程师，主要研究方向为配电网规划；

汤向洋(1977)，男，助理工程师，主要研究方向为电力系统继电保护。