基于随机机会约束规划的有源配电网多目标规划
2015-06-21屈高强李荣董晓晶康健党东升刘洪
屈高强,李荣,董晓晶,康健,党东升,刘洪
(1.国网宁夏电力公司经济技术研究院,银川市750011;2.天津大学电气与自动化工程学院,天津市300072;3.国网宁夏电力公司,银川市750010)
基于随机机会约束规划的有源配电网多目标规划
屈高强1,李荣2,董晓晶1,康健3,党东升1,刘洪2
(1.国网宁夏电力公司经济技术研究院,银川市750011;2.天津大学电气与自动化工程学院,天津市300072;3.国网宁夏电力公司,银川市750010)
含分布式新能源配电网规划均采用被动、保守接入分布式新能源的规划方法,固然保证了配电网安全,但并没有反映分布式新能源的出力特征,因而造成不必要的配电网建设投资。为了解决这一问题,采用基于随机机会约束规划的有源配电网规划方法,将有源配电网规划中必须满足的硬性约束条件转变为较高置信度的软约束形式,同时,在模型中引入反映经济效益的投资成本、网络损耗以及反映配电网供电安全性的电压偏移度这3个目标函数作为优化对象,形成了有源配电网规划的多目标随机机会约束规划模型。采用结合量子法改进的非支配排序多目标优化遗传算法(non-dominated sorting genetic algorithm2,NSGA-2)求解获得非劣解帕累托前沿,在此基础上,运用逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS)对非劣解排序得到最优方案。最后,以57节点的配电网网络为算例,验证了方法的可行性、有效性。
随机机会约束;分布式电源;时序特性;有源配电网规划;改进NSGA-2
0 引 言
可再生能源的分布式发电(distributed generation,DG)能够对能源进行就地消纳,与集中式发电相比,在有效减少网络损耗、电网灾变时支撑局部供电等方面具有突出优点。然而,由于DG的接入,配电网的短路电流、节点电压、线路潮流等运行指标都会受到较大的影响,在含分布式新能源配电网规划中充分考虑分布式新能源出力的不确定性,降低分布式新能源对配电网节点电压、线路潮流等方面的负面影响,提升配电网运行的经济性对分布式新能源的发展具有十分重要的意义。
目前,在含分布式新能源的配电网规划研究中,根据规划对象的不同划分为仅对配电网中分布式新能源的规划和分布式新能源与配电网网络规划的综合协调规划。仅对配电网中分布式新能源的规划是以配电系统网络为已知的边界条件,对分布式新能源在配网中的位置和容量大小进行优化[1-3];综合协调规划是同时对配电网网络布局与分布式新能源的位置容量进行综合规划,属于配网全局优化[4-6]。然而,目前在含分布式新能源配电网的规划中,分布式新能源均以一种较为保守的方式接入配电网,虽然能够有效保证配电网运行中各项指标在安全的范围之内,但没有体现出可再生能源出力的随机概率特征,必然导致投资的浪费,不利于可再生能源的积极发展。为此,本文提出基于随机机会约束规划的有源配电网网络规划方法,基于分布式新能源发电出力的概率特性,将配电网规划中的硬性约束条件转化为软性约束条件并综合考虑经济性和安全风险两者的关系,使分布式新能源安全经济地接入到配电网中。另外,本文构建的是综合考虑投资成本、网络损耗以及电压偏移度的多目标有源配电网规划模型,将全局寻优能力较强的量子变换与典型多目标求解算法非支配排序多目标优化遗传算法(non-dominated sorting genetic algorithm 2,NSGA-2)相结合,增强NSGA-2的全局寻优能力,得到规划模型分布较为均匀的Pareto解集,进而由逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS)综合评价法选定规划模型最优解。
1 机会约束规划
机会约束规划要求约束条件以一定的置信度成立,能够更准确地表示规划问题中的不确定因素,由于规划问题中的一些不满足约束条件的极端情况出现的概率很低,为避免配电网规划方案偏于保守,机会约束规划方法将约束条件中的硬性约束转化为软性约束[7-9],使约束条件以一定的置信度水平成立。机会约束规划的一般形式为
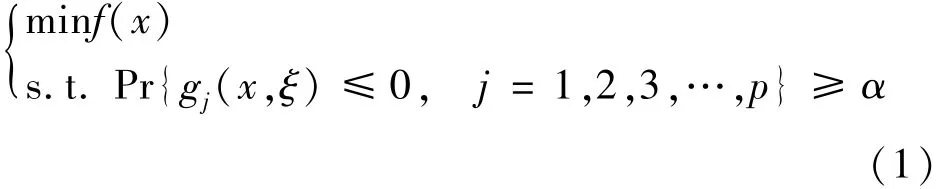
式中:f(χ)是目标函数;gj(χ,ξ)是约束函数,ξ为已知其概率分布的随机向量;Pr{gj(χ,ξ)≤0,j=1,2,3,…,p}≥α为软性约束条件,Pr{·}表示{·}中事件成立的概率,α为给定的约束条件置信水平。
式(1)表示的是联合机会约束,即各约束条件的置信水平一致,更为一般的是下面的混合机会约束,各约束条件具有不同的置信水平,即

2 考虑时序特性的概率潮流计算
2.1 DG不确定模型
风机、光伏阵列的出力时序特性与规划地区的风速、光照强度变化有直接关系。地理学研究表明,不同季节风速、光照强度日变化差异明显[10]。根据气象资料可得到不同季节的风速时序特性曲线如图1,光照强度特性曲线如图2,由此可计算出风机、光伏阵列的出力。负荷时序模型采用式(3)[11]进行计算,据此可做出负荷时序特性曲线如图3。

式中:Lp为负荷点年负荷峰值;Lpw为周负荷曲线与年负荷峰值的比值;Lpd为日负荷曲线与周负荷峰值的比值;Lph为日负荷曲线与日负荷峰值的比值。

图2 光照强度时序特性曲线Fig.2 Timing characteristics curve of illumination intensity

图3 负荷时序特性曲线Fig.3 Timing characteristics curve of load
显然风速和光照强度时序上具有互补特性,如冬季风速较大,而光照强度较弱;夏季风速较小,而光照强度较强。又如10:00~15:00风速较小,光照强度较强;00:00~5:00光照强度为0,而风速较大。负荷与DG出力具有耦合性,且峰值负荷与DG最大出力不具有同时性,峰值负荷出现在19:00左右,而风速在03:00左右最大,光照强度在12:00时最大。因而确定性DG出力模型、负荷模型或仅考虑随机性的DG出力模型、负荷模型难以真实地反映配电网实际指标。
本文依照风速、光照强度及负荷的时序特性曲线将1年依季节划分为春夏秋冬4个场景,每天划分为3个时段,01:00~06:00和23:00~24:00为第一时段,07:00~09:00和18:00~22:00为第二时段,10: 00~17:00为第三时段。则1年划分为12个典型场景。
2.2 DG出力与负荷的随机模型
利用威布尔分布[11]描述各场景中的风速随机性,将风速的概率密度曲线和风速与出力之间的关系函数相结合即可得到风机出力的随机分布。威布尔分布的概率密度函数可表示为
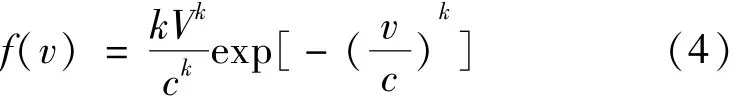
式中:v为风速;k和c为威布尔分布函数的形状因子和尺度因子,可由不同场景中风速的均值和方差求得。
风力输电功率Pwind与风速v之间的关系为
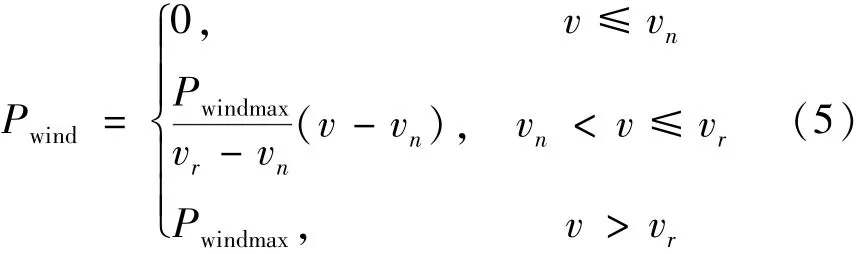
式中:Pwindmax为风机的额定功率;vr为风机的切入风速;vn为风机的额定风速。
在不同场景的一些时间段内,光照强度[10]可近似看成Beta分布,其概率密度函数可表示为
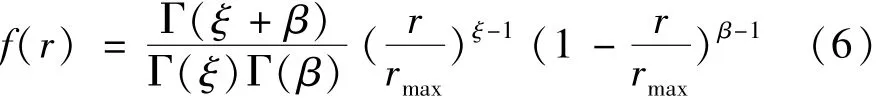
式中:r和rmax分别表示这一时间段内的实际光照强度和最大光照强度;ξ和β均为Beta分布的形状参数,可由不同场景下的光照均值和方差求得。
太阳能发电功率Ppv和光照强度r之间的函数为
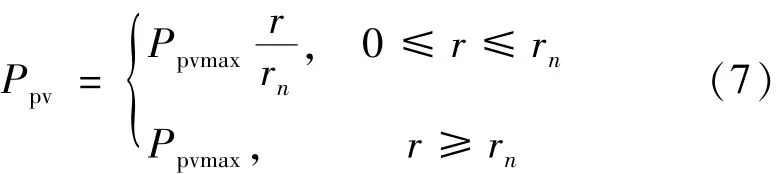
式中:Ppvmax为光伏阵列的额定功率;rn为额定光照强度。
负荷的概率分布采用正态分布,即

式中ϑi(t)、(t)分别为第t个场景中第i个节点负荷的期望值、方差值。
2.3 考虑时序特性基于半不变量的随机潮流计算
依历史数据可以分别得到12个场景负荷和风机光伏出力的概率分布情况,进而得到其各阶半不变量。采用半不变量与牛顿-拉夫逊潮流计算相结合的概率潮流方法进行潮流计算[12-13]。
电力系统的潮流计算方程为

式中:W表示节点注入量;X表示节点状态变量。将第t0个场景潮流方程在基准运行点线性化
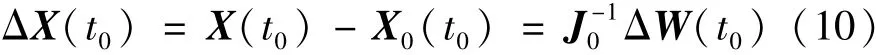
式中:X(t0)为第t0个场景的状态变量在基准运行状态的期望;J0为雅各比矩阵。
依上式可知采用半不变量法即可由ΔW(t0)的各阶半不变量得到ΔX(t0)的各阶半不变量,再利用Gram-Charlier级数展开即可求得第t0个场景的随机变量的分布函数。
3 含DG配电网随机机会约束规划模型
分布式新能源出力具有随机概率特性[14],在配电网规划的约束条件中含有分布式新能源出力的随机变量,因此,本文以规划方案的投资最小为目标,将规划模型中的硬性约束条件转化为软性约束,建立配电网随机机会约束规划模型。
3.1 配电网投资建设成本最小
配电网投资建设成本的最小值为

式中:n是主干线路回数;n′是分支线路回数;Lmain,i是第i回主干线路的长度;C0,i是第i回主干线路类型的单位长度投资;Lbranch,j是第j回分支线路的长度;C′0,i是第j回分支线路类型的单位长度投资;Cd为位于线路起始点断路器的费用;Cf是线路环网开关(负荷开关或环网柜)的投资;Ch是组网环网柜的投资(针对“N-1”单环网的接线方式,每个“N-1”单环网都有1个组网环网柜)。
3.2 配电网网络损耗最小
不同的配电线路网络布线会导致配电网络潮流分布的不同,随之将引起配电系统网络损耗发生变化。以网络损耗最小建立目标函数。配电系统网损最小目标为

式中:Ploss表示配电系统网络损耗;χi表示待选线路i是否被选中投入建设,若是则为1,否则为0;PL、QL分别为各负荷节点的有功负荷,无功负荷;PDG、QDG分别为接入的分布式新能源有功容量和无功容量。
3.3 负荷节点电压偏移量最小
负荷节点电压偏移量为

式中:ΔU为负荷节点偏移量;Ul为节点l实际电压;UlE为期望电压值;ΔUmaxl为最大允许电压偏差,节点l原始负荷,Plode为配电系统总负荷。
3.4 约束条件
(1)节点电压约束。

(2)支路传输功率约束。

(3)系统潮流等式约束。

式中:Pi、Qi为节点i处有功、无功注入;Ui、Uj为节点i、j电压幅值;Gij、Bij为支路ij的电导、电纳;θij为节点i、j间电压相角差。
(4)DG出力约束。
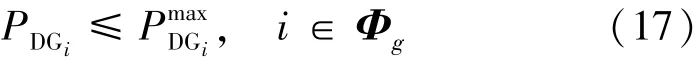
式中:PDGi为在节点i处DG提供的有功功率;为在节点i处允许DG提供的最大容量。
4 融合量子进化的改进NSGA-2求解方法
本文基于量子计算原理和多目标进化理论,改进了对NSGA-2算法,采用量子位编码,充分利用量子位的概率特性、量子态干涉特性进行概率交叉和混沌变异,提高寻优效率和收敛速度;在基于非支配排序、精英保留和分层聚类等多目标优化策略保持种群多样性的同时,保证进化向Pareto全最优解集方向进行。
另外,在初始化网络及遗传的交叉变异过程中会产生大量不连通方案,不利于初始种群在可行域的均匀分布,本文采用一种吸收孤立节点的保证连通性初始化方法[15]。现状网络考虑为由一个连通的大系统和若干孤立节点以及小孤岛所组成,吸收孤立节点初始化方法的主要的流程为:
(1)将系统节点分为连通大系统集合C={Ni}和孤立节点集合DC={Nj}。
(2)判断是否存在大系统外的小孤岛,若不存在,则转步骤(4)。
(3)删除小孤岛所包含的已有线路,将小孤岛节点转化为孤立节点。
(4)顺序取Nj∈DC,搜索Nj与任何Ni∈C之间的可架线走廊,若无可架线走廊,j=j+1,转(4)。
(5)随机选取1条Nj与Ni的可选走廊,在可增回数限制内随机对架线回数赋值。
(6)将节点Nj由集合DC转至集合C。
(7)判断集合DC是否为空,若不为空,转步骤(4)。
(8)以步骤(3)中删除的孤岛线路替代对应走廊的随机线路,结束。
4.1 量子位染色体实数编码
采用实数量子位来表示变量,量子位实数编码的染色体结构表示为

式中qi为种群的1个染色体,j=1,2…n为空间维数。每个染色体具有2个信息,包括实数位置和相角。
4.2 染色体更新
对染色体的更新通过量子旋转门实现,其工作原理为

式中:(αi,βi)为染色体中第i个量子比特;θi=s(αi,βi)Δθi,s(αi,βi)和Δθi的值根据某一策略事先确定,以表格的形式查询。
4.3 最优方案的确定
本文利用TOPSIS[16]对帕累托前沿中的个体进行排序,得到问题的最优解。定义“虚拟最优解”为各个子目标函数均取可行域内最优值的虚拟解。“虚拟最劣解”为各个子目标函数均取可行域内最劣值的虚拟解。此处将可行域视为帕累托前沿中所有个体所构成的集合。由于各子目标之间的互斥性,虚拟解一般不存在于可行域内。基于TOPSIS的决策过程如下。
(1)原始矩阵归一化处理:
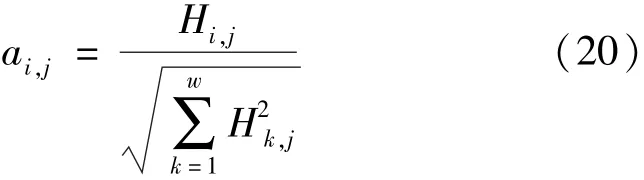
式中:Hi,j为第i个解的第j个子目标函数值;w为帕累托前沿中的个数总数;ai,j为Hi,j归一化后的值。
(2)得到“虚拟最优解”和“虚拟最劣解”归一化后的解向量,“虚拟最优解”为A+=[a1+,a2+,…,an+],“虚拟最劣解”为A-=[a1-,a2-,…,an-]。
(3)计算非劣解与A+及A-之间的距离和
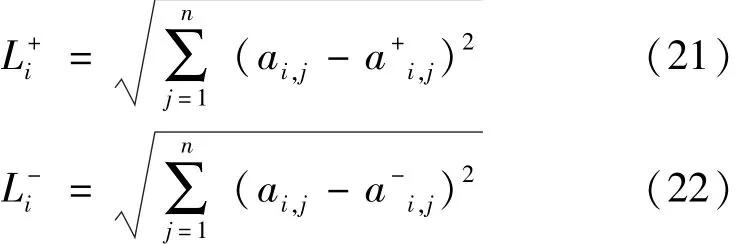
(4)计算各个解与虚拟最优方案的接近程度Mi:
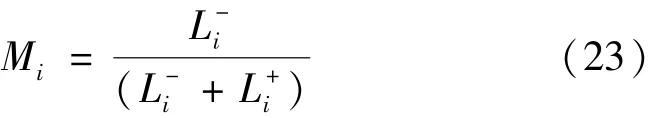
由式(23)可知Mi是小于1的正数,根据Mi大小进行排列,Mi的大小表示解的优劣程度。
5 算例分析
5.1 算例概况
采用上述配网规划模型和方法,对待规划的配电网进行了以DG为边界条件的配电网络扩展规划。图4中,实线表示已建成线路,规划中将不进行改造;虚线表示规划中的待选线路。节点1到节点3为配电站节点,节点33到节点57为新增加的负荷节点。

图4 待规划配电网络Fig.4 Distribution network to be planned
本算例主要解决的问题为在分布式新能源位置与容量确定的情况下采用机会约束规划对配电网络进行扩展规划。分布式电源指定的位置和容量如表1所示。

表1 规划后分布式电源位置和容量信息Table 1 Position and capacity information of distributed generation after planning
单个分布式电源的容量为100 kVA,分布式电源功率因数取0.9,算例中采取的风机参数如下:切入风速为3 m/s;额定风速为14 m/s;光伏组件选取PILKINGTON SFM144Hx250wp型,每个组件面积为2.16 m2;光电转换效率为13.44%;1个光伏阵列的组件个数为400个。为简单起见,节点电压与支路潮流约束的置信水平一致,取0.8与1这2种情况。
5.2 结果分析
对图4所示配电系统设定约束条件的置信度为0.8时,利用改进的NSGA-2对模型求解,得到最优的30个方案,其帕累托前沿的分布如图5所示。

图5 多目标优化的Pareto前沿Fig.5 Pareto frontier of multiple-object optimization
图5所示的Pareto前沿是在处理器为Intel(R) Core(TM)E7500、内存为2G的台式机上经826.73 s运行所得。对各个目标单独优化得到其最优解分别为0.0388 MW,144.163万,0.378 9,则“虚拟最优解”的目标函数向量为A+=[0.388,144.163,0.378 9]。
同样,在单独优化中根据记录数据可知其最劣解分别为0.829 MW,226.609万,0.991 2,则“虚拟最劣解”的目标函数向量为A-=[0.829,226.609,0.991 2]。
利用TOPSIS筛选出最优的3个方案,见表2。

表2 方案比较Table 2 Network optimization results of scheme 3
由表2对比可知,在配电网规划中,可根据规划者的经验和规划区域不同的要求进行方案的选择。若目标网络更注重减小损耗,提高配电网络运行的经济性,则可选择方案1作为最终规划方案;若规划者更希望电压偏移量较小,使配电网运行更加安全可靠,则可以选择方案3。本文优先考虑电压偏移量与网络损耗,选择投资费用比方案2多12万元的方案3为最终规划结果,如图6示。
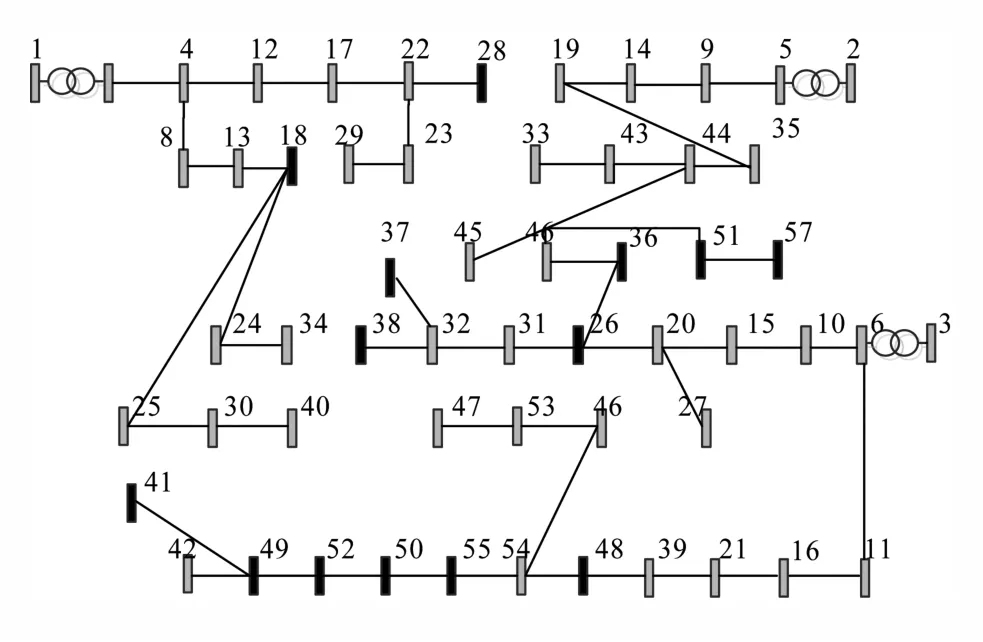
图6 方案3网络优化结果Fig.6 Network optimization results of scheme 3
由于DG的接入,配电网网络中各条线路上的节点电压会相应增加,在配电网线路的不同位置接入相同容量的DG导致的各节点电压分布差别较大,DG并网位置越接近线路尾节点对节点电压分布的影响越大,而在线路偏尾端的位置接入DG可适当降低网络损耗。当电压约束条件置信度降低时,规划结果更趋向于将分布式电源置于线路的中末端以降低网络损耗成本,与图3中的网络布局结果较为吻合。
当置信度取1,即对分布式新能源的接入采用最安全的策略,则采用改进NSGA-2法进行求解,并利用TOPSIS从帕累托前沿中筛选出最优解,与置信度为0.8时最优解对比如表3所示。
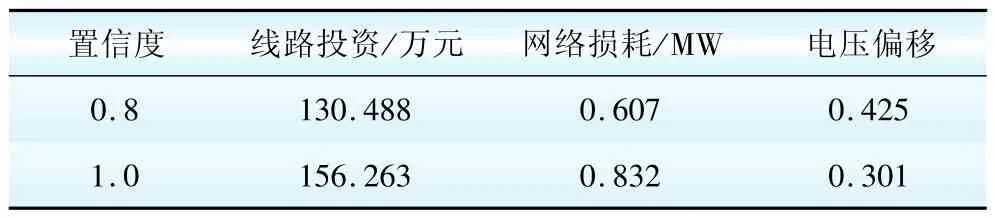
表3 方案比较Table 3 Scheme comparison
可见,规划的线路投资费用与网络损耗随着置信度的提高而增大,电压偏移却有所降低。当置信度水平为0.8时,规划方案充分考虑了DG和负荷波动的概率特性,在保障配电网运行安全性的同时有效降低了线路投资和网络损耗;采用置信度为1的保守规划策略,电压偏移量略低,安全性较高,但是造成了不必要的投资浪费和网络损耗。
6 结 论
(1)综合考虑随机和时序特性能更真实地反映配电系统运行情况,相应的规划方案也更符合实际。
(2)采用随机机会约束规划,将硬性约束条件以一定置信度的形式转化为软性约束条件,可在保证配电网安全运行的前提下有效降低线路投资与网损。
(3)采用多目标规划模型,得到非劣解的帕累托前沿,采用TOPSIS对方案进行排序,在优选出来的方案中进一步选择最终方案时,可以根据规划者和规划地区的具体情况做出选择。
[1]Wang Caisheng,Nehrir M H.Analytical approaches for optimal placement of distributed generation sources in power systems[J]. IEEE Transactions on Power Systems,2004,19(4):2068-2076.
[2]陈海焱.含分布式发电的电力系统分析方法研究[D].武汉:华中科技大学,2008.
Chen Haiyan.Study on analysis methods in power systems with distributed generation[D].Wuhan:Huazhong University of Science&Technology,2008.
[3]Harrison G P,Piccolo A,Siano P,et al.Hybrid GA and OPF evaluation of network capacity for distributed generation connections [J].Electric Power Systems Research,2008,78(3):392-398.
[4]王成山,陈恺,谢莹华,等.配电网扩展规划中分布式电源的选址和定容[J].电力系统及其自动化,2006,30(3):38-43.
Wang Chenshan,Chen Kai,Xie Yinghua,et al,Siting and sizing of distributed generation in distribution network expansion planning [J].Automation of Electric Power Systerms,2006,30(3):38-43.
[5]Brown R E,Pan Jiuping,Feng Xiaoming,et al.Siting distributed generation to defert&dexpansion[C]//Proceedings of the IEEE PowerEngineeringSocietyTransmissionandDistribution Conference.Atlanta,GA:IEEE,2001,2:622-627.
[6]Charnes A,Cooper W W.Chance-constrained programming[J]. Management Science,1959,6(1):73-79.
[7]Liu B,Iwamura K.A note on chance constrained programming with fuzzy coefficients[J].Fuzzy Sets&Systems,1998,100(97):229-233.
[8]Liu B.Minimax chance constrained programming models for fuzzy decision systems[J].Information Sciences,1998,112(1-4): 25-38.
[9]何乃光.渤海湾海路风速日变化对比分析[J].气象,1980(4): 30-32.
HeNaiguang.ComparativeanalysisofBohaibayseawind speedchanges[J].Atmosphere,1980(4):30-32.
[10]葛少云,王浩鸣,王源山,等.含分布式风光蓄的配电系统可靠性评估[J].电力系统自动化,2012,36(5):16-23.
Ge Shaoyun,Wang Haoming,Wang Yuanshan,et al.Reliability evaluation of distribution system including distributed wind energy,solar energy and battery storage[J].Automation of Electric Power Systems,2012,36(5):16-23.
[11]王成山,郑海峰,谢莹华,等.计及分布式的发电的配电系统随机潮流计算[J].电力系统自动化,2005,29(24):39-44.
Wang Chenshan,Zheng Haifeng,Xie Yinghua,et al.Probabilistic power flow containing distributed generation in distribution system [J].Automation of Electric Power Systems,2005,29(24): 39-44.
[12]余昆,曹一家,陈星莺,等.含分布式电源的地区电网动态概率潮流计算[J].中国电机工程学报,2011,31(1):20-25.
Yu Kun,Cao Yijia,Chen Xingying,et al.Dynamic probability power flow of district grid containing distributed generation[J]. Proceedings of the CSEE,2011,31(1):20-25.
[13]高军彦,麻秀范,凡鹏飞.计及分布式发电的配电网协调规划整体框架与模型[J].电网与清洁能源,2008,24(4):12-16.
Gao Junyan,Ma Xiufan,Fan Pengfei.A global framework and model ofdistributionnetworkcoordinatedplanningincluding distribution generation[J].Power System and Clean Energy. 2008,24(4):12-16.
[14]王一,程浩忠.计及输电阻塞的帕累托最优多目标电网规划[J].中国电机工程学报,2008,28(13):132-138.
Wang Yi,ChengHaozhong.Paretooptimalitybasedmultiobjective transmission planning considering transmission congestion [J].Proceeding of the CSEE,2008,28(13):132-138.
[15]何逢标.综合评价方法MATLAB实现[M].北京:中国社会科学出版社,2010:316-325.
[16]尹建兵.配电网规划研究[D].杭州:浙江大学.2011.
Yin Jianbing.Study on distribution network planning[D]. Hangzhou:Zhejiang University,2011.
(编辑:蒋毅恒)
Multiple-Objective Planning of Active Power Distribution Network BaseOd on Random Chance Constrained Programming
QU Gaoqiang1,LI Rong2,DONG Xiaojing1,KANG Jian3,DANG Dongsheng1,LIU Hong2
(1.State Grid Ningxia Electric Power Science Research Institute,Yinchuan 750011,China;2.School of Electrical Engineering and Automaton,Tianjin University,Tianjin 300072,China;3.State Grid Ningxia Electric Power Corporation,Yinchuan 750010,China)
Most of the typical distribution network programmings with distributed new energy utilize passive,conservative programming method to access distributed new energy,which indeed secure the safe of distribution network,but cannot reflect the output characteristics of distributed new energy and cause unnecessary investment on distribution network construction.To solve this problem,this paper proposed active power distribution network programming method based on random chance constrained programming.Firstly,the hard constraint conditions in active power distribution network programming were transformed into soft ones with higher confidence level.Meanwhile,three independent objective functions including the investment cost reflecting the economic benefit,the power loss and the voltage deviation degree reflecting the distribution network power supply security were set to form the multiple-objective active power distribution network planning model based on random chance constrained programming.Then,the model was solved to obtain noninferior solution Pareto frontier by the improved NSGA-2(non-dominated sorting genetic algorithm2)combined with the quantum method.On this basis,the TOPSIS(technique for order preference by similarity to ideal solution)was used to sort the non-inferior solution,in order to obtain the optimal solution.Finally,a distribution network with 57 nodes was used as example to verify the feasibility and availability of the proposed method.
random chance constraint;distributed generation;time sequential characteristics;active power distribution network planning;improved NSGA-2
TM 715
A
1000-7229(2015)11-0010-07
10.3969/j.issn.1000-7229.2015.11.002
2015-06-15
2015-08-10
屈高强(1983),男,本科,工程师,主要从事电力系统规划及分析研究工作;
李荣(1991),男,硕士研究生,主要研究主动配电网规划;
董晓晶(1980),男,本科,工程师,主要从事电力系统及电网规划工作;
康健(1979),男,本科,工程师,主要从事配电网规划及新能源接入管理工作;
党东升(1982),男,本科,工程师,从事继电保护工作;
刘洪(1979),男,博士,副教授,主要从事城市电网规划、评估等方面的研究和应用工作。
国网宁夏电力公司科技项目(5229JY1307G6)。
