基于COA-EO混合算法的含DG的配电网Pareto最优规划
2015-06-21曾鸣彭丽霖樊倩男李冉
曾鸣,彭丽霖,樊倩男,李冉
(华北电力大学经济与管理学院,北京市102206)
基于COA-EO混合算法的含DG的配电网Pareto最优规划
曾鸣,彭丽霖,樊倩男,李冉
(华北电力大学经济与管理学院,北京市102206)
含DG的配电网规划是一种复杂的组合优化问题,随着智能配电网的发展以及波动性可再生能源的接入,对优化模型的效率提出了更高的要求。该文提出了基于混沌优化算法(chaos optimization algorithm,COA)和极值动力学优化算法(extreme dynamics optimization algorithm,EO)相互结合的多目标问题求解模型。通过算例验证,结果表明COA-EO优化算法同时利用COA算法和EO算法的优点,从而成功避免了各自缺陷,使得普通EO算法跳出局部最优,避免了算法的早熟现象,从而得到了全局最优结果。另外,为得到更好的多目标优化结果,引入Pareto最优解,并利用所提出的COA-EO算法求解Pareto最优解。计算结果亦表明COA-EO算法的优化性能优于EO算法、遗传(genetic algorithm,GA)算法、蚁群(ant colony optimization,ACO)算法、ACO-EO算法和GA-EO算法,说明COA-EO算法是解决含DG配电网规划问题的有效工具。
配电网规划;分布式电源;可再生能源;COA-EO混合优化算法;Pareto最优解
[编者按]在智能电网和最新最热的能源互联网中,配电网都处于关键地位,是分布式能源、互动用户等新事物与传统电力系统间的纽带,同时也是电力系统中变革最大的部分。20年来,配网投资比例大幅上升,国家又新推出了2万亿的建设改造行动计划。既要规划好发展蓝图又要利用好巨额投资,现在的配电网规划具有历史使命,并充满新的内容和挑战。基于此,本刊特邀天津大学肖峻老师担任本期“配电网规划专栏”特约主编。
本专栏稿件内容非常丰富新颖,涉及到含源配网规划、二次保护配置规划、一次网架与二次信息系统协同规划、二次完善后一次系统供电能力的发挥、以及容载比标准降低的探讨,还有一些各具特色的实践分享,包括北京的世界一流配网指标体系、天津生态城的多元能源互联智能配网、福建中低压配网评估提出的公共服务价值、珠海的环保规划方法等。
0 引 言
当前,以清洁能源开发利用为特征的新一轮能源革命正在推动第三次工业革命孕育发展,由智能电网、分布式电源、电动汽车充换电设施等构成的“能源互联网”势在必行,发展智能配电网对于促进我国战略性新兴产业发展和经济转型升级具有广泛的带动作用,对承载和推进国家“互联网+”智慧能源战略具有重要意义[1]。智能配电网的发展,对配电网规划提出了更高的要求。对于含DG的配电网规划,科学高效的规划方法能够使DG更好地接入到配电网,同时能够实现大规模间歇性可再生能源的兼容,并通过合理的DG调度实现能源结构的优化以及系统的最优潮流运行[2-4],同时提升配电网资产利用空间,延缓网络升级投资。此外,分布式电源的大规模整合也为传统的配电网规划带来了一些影响,主要表现在以下几方面[5-6]:1)在规划的过程中需要考虑DG的选址和定容以及DG接入容量的限制;2)大量DG的接入使得负荷预测工作更加困难;3)部分DG的输出功率(如太阳能、风能)具有明显的不确定性,不适合进行传统电源的规划。因此,传统的配电网规划方法已经不再适用于智能配电网发展背景下含DG的配电网规划问题。
含DG的配电网规划是一种复杂的组合优化问题[7],近年来,诸多研究者致力于利用不同的方法求解出更好的优化结果。这些方法的最主要特征就是在目标函数的选取上只有单目标和多目标2种。单目标方程是基于考虑成本、效益、可靠性、安全性、容量等其中的一个目标;单目标方程及其约束条件易于求解、计算简单,但单目标方程无法满足日益增长的多方面需求。多目标方程是考虑上述目标中的2个或2个以上的目标,是当前研究配电网规划的重点;多目标函数的求解方法可以大体上归纳为2种:基于数学规划算法以及启发式算法。数学规划算法多借助混合整数线性规划(mixedintegerlinear programming,MILP)进行求解。文献[8]统筹考虑损耗、发电机成本和线路安全约束等条件,将MILP应用于输电扩容规划问题。通过IEEE 24总线系统以及118节点测试系统的模拟,验证了该方法的准确性和高效性。文献[9]借助MILP方法求解包含初级和次级电网在内的配电网的优化规划问题。将该模型应用于测试系统,结果表明其对配电网的规划设计有一定帮助。文献[10]将MILP应用于分布式电源规模和选址的优化问题,且计算结果表明该方法可以得到相应的优化结果。
当目标函数及约束条件的规模较小时,MILP能够得到最优结果;反之,当目标函数及约束条件复杂程度较高、规模较大时,MILP就不能解决多目标优化问题。此时,启发式算法由于其可以确保求得最优解,因而多应用于复杂和非线性多目标函数问题的求解。文献[11]借助改进的粒子群算法求解配电网中存在多个分布式电源的网架最优。文献[12]提出了人工蜂群算法,在尽可能减少线路损耗的基础上确定DG机组的最优规模,功率因数和位置。文献[13]提出了改进的分析方法,用以计算DG的最优规模,并确定DG所处的最优位置。上述方法通过三分布测试系统进行测试,并与其他方法相比,证明了改进的分析方法的有效性。大多数启发式算法,如遗传(genetic algorithm,GA)算法,粒子群算法,人工蜂群算法等在解决大规模、复杂程度较高的多目标优化问题时都会出现由于参数数目的庞大导致难以计算、易陷入局部最优、难以达到全局最优的问题。
为了解决上述问题,本文提出了一种基于极值动力学优化算法(extremedynamicsoptimization algorithm,EO)和混沌优化算法(chaos optimization algorithm,COA)的配电网规划算法,旨在最小化投资成本、线路损耗成本以及最大化DG的安装容量。EO算法可调节参数较少(或者没有),并且具有很强的收敛能力和局部搜索能力,但全局搜索能力较差;而COA算法具有强大的全局搜索能力,但容易陷入局部最优,因此,将EO算法和COA算法相互结合,能够达到优势互补,避免自身的缺陷的目的,从而提高算法的优化性能。另外,为得到更好的多目标优化结果,本文引入Pareto最优解,并利用所提出的COA-EO算法求解Pareto最优解。
1 规划模型建立
1.1 目标函数
考虑DG的配电网优化就是在传统配电网规划的基础上,以投资和运行费用最小为目标,为满足负荷增长的需求,从而制定电网升级增建新的配电网网络线路以及在适当的位置安装DG[14]。一般地,含DG的配电网规划的目标函数应包含:投资费用、损耗费用、分布式能源安装容量以及对环境产生的影响;本文默认DG为环保型电源,不计入总目标函数,具体的目标函数如下所示:

式中:Zinvestcost为投资费用,包括线路投资和DG投资;Cli为新建线路i的投资费用;CDGj为第j个分布式电源的投资费用;q1,q2分别为线路和分布式电源的年平均费用系数;N1为线路数量;nDG为分布式电源数量;cDG为单位运行成本;cb为单位购电价格;PDGj为第j个DG电源的额定容量;T0为DG年最大运行时间;Zlosscost为网络损耗费用,包括DG电源的损耗Ploss和线路损耗为单位电价;Tmax为第i条线路的年最大损耗小时数;ΔPli为线路i的有功损耗;为分布式电源安装容量最大的目标函数。
目标函数需满足以下限制条件:
(1)节点电压约束:Uimin≤Ui≤Uimax,i=1,2,…,n。Ui为节点i的电压;Uimax、Uimin分别为节点电压的上限和下限。
(2)导线电流约束:Ii≤Iimax,i=1,2,…,n。Ii为节点i的电流;Iimax为节点i电流的上限。
(3)分布式电源容量约束:PDGj≤Pj,∑PDGj≤Pmax;其中PDGj和Pj分别为第j个分布式电源的装机容量和节点负荷;Pmax为系统允许的最大接入容量。
(4)分布式电源接入总量约束:PDG≤Pn× 20%。PDG为分布式电源安装的总容量;Pn为新增负荷总量。
(5)配电网网架须呈辐射状结构。
1.2 分布式发电输出功率的计算
分布式电源的功率输出具有随机波动性,主要与地理环境、气象等自然因素相关。本文主要计算风能发电和太阳能发电的功率输出,根据自然环境和历史数据,采用蒙特卡罗方法对DG发电出力进行模拟。1.2.1 风力发电输出功率计算
针对风速的研究认为风速具有统计特征,呈现正偏态分布;用于描述风速分布的函数或者曲线有很多种,其中威布尔分布曲线被广泛采用。风机输出功率的概率密度函数公式[15]如下所示:

式中:K为形状参数;C为尺度参数;a=Prvci/(vci-vr),b=Pr/(vr-vci);Pr为风机额定功率;vci为风机切入风速;vr为风机额定风速。
另外,如果风速呈现正态分布,则风机输出功率的概率密度函数为
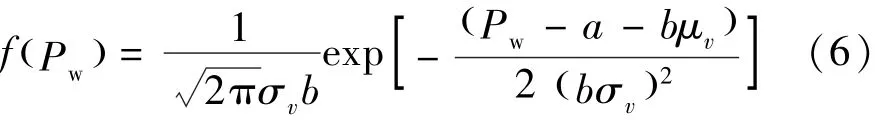
式中:μv、σv分别是风速的均值和方差。
1.2.2 光伏发电输出功率计算
光伏发电的输出功率与光照强度I、光伏电池的面积S以及光电转化效率η密切相关,其输出功率Ps=ISη。假设光照强度在一定时间内服从Beta分布,则光伏发电系统输出功率的概率密度函数为
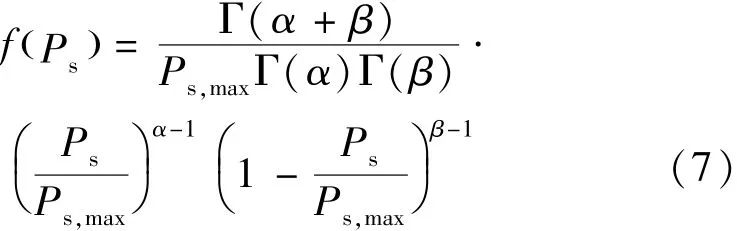
式中:Ps,max为光伏阵列的最大输出功率;α、β为形状参数。
1.3 Pareto最优解的定义
通常,将多目标优化中的最优解称为Pareto最优解。在多目标优化问题中,通常具有很多个Pareto最优解,但多目标优化问题只能接受其中的一个“满意解”,在提高任何目标函数某个最优性能的同时,会降低其他目标函数的最优性能[16]。一般地,对Pareto最优解的描述如下。
定义1 假设求解多目标最小化问题(最大化问题可通过去相反数或者倒数进行转化),则多目标优化问题的数学模型可以描述如下:
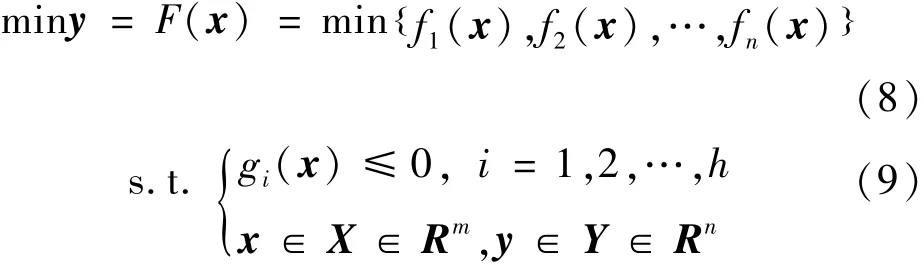
式中:x为决策变量;X为x形成的决策空间;y为目标变量;Y为y形成的目标空间;gi(x)≤0为x需要的h个约束条件。
定义2 Pareto支配
假设Xf={f1(x),f2(x),…,fn(x)}为多目标问题的可行解空间,定义解u=(u1,u2,…,un)的支配解v=(v1,v2,…,vn),记为u>v,当且仅当满足:

定义3 若搜索空间中不存在任何其他解x′支配解x(x′>x),则x称为Pareto最优解;将多目标优化问题中全部的Pareto最优解的集合称为Pareto最优解集;Pareto最优解集的目标值构成的区域称为Pareto最优前沿。
2 优化算法
2.1 基本EO算法
极值动力学优化算法是在Boettcher和Percus提出的Bak-Sneppen生物演化模型的基础上提出的一种局部搜索启发式算法。EO算法与大多数进化算法不同,其研究对象只有单个个体或者单个染色体,而个体内部的组元为基因或者基因片段,因此,系统的组成是由个体的所有组元构成。EO算法可以看成是通过不断的自我完善,改变个体中适应度最差的组元,使得个体总是朝着最优的结构演化;同时,通过改变与最差组元相邻的组元,使得整个系统能够协同进化,个体的构造得到不断的优化,最终可以找到优化问题的近似最优解或者最优解[17]。EO算法收敛速度快,局部搜索能力强,而且无可调参数,因此将EO算法应用于优化问题时设计简单,容易实现。
对于最基本的优化问题(以极小化问题为例),EO算法的一般流程如下所示。
(1)随机产生一个个体I=(x1,x2,…,xn),假设迄今为止找的最优解为I∗,其目标函数值为Z(I∗),则初始的I∗=I,Z(I∗)=Z(I);
(2)对于当前的个体,计算每个组元xi,i=1,2,…,n的适应度函数值λi;
(3)对所计算出的n个适应度数值{λ1,λ2,…,λn}进行排序,找出适应度值最小的组元xj,若xj≤xi,则xj为最差组元;
(4)在当前个体I的领域中选择一个相邻个体I′,使得最差组元xj发生改变,并无条件地接受I=I′;
(5)若当前的目标函数值Z(I)小于迄今为止最优目标函数值Z(I∗),则令I∗=I,Z(I∗)=Z(I);
(6)判断是否满足终止条件,若不满足,则重复步骤(2)~(5),否则,跳出循环并返回最优解I∗和最优目标函数值Z(I∗)。
从上述EO算法的流程中可以看出,基本EO算法在寻优时不需要调节任何参数,降低了算法的计算维度和复杂程度,因此,基本的EO算法操作简单,收敛速度快,免去了调参的麻烦。目前鲜有文章将EO算法应用于电力系统规划问题中,因此,本文根据EO算法的特点,将其应用于求解计及分布式电源的配电网规划问题中,具有较大的潜力。然而,EO算法在求解优化问题时被发现与其他传统优化算法相比(如GA、ACO等),虽然计算过程简单、能够较快收敛,但其容易陷入局部最优;为克服这个缺点,许多学者对EO算法做出改进,如Boettcher和Percus为基本EO算法引入了可调参数,从而提出了改进的优化算法,避免了在求解组合优化问题时容易陷入局部最优的情况。另外,改进的EO算法还有通用EO算法、连续EO算法等;这些算法被证实在求解最优化问题中一定程度上避免了EO容易陷入局部最优的问题,但将EO算法或者改进的EO算法应用于多目标优化问题方面的研究并不多。
为求解所提出的考虑DG的配电网规划问题,本文将混沌优化算法和EO算法相结合,形成COA-EO优化模型。由于混沌具有遍历性,利用混沌变量进行优化搜索会比盲目无序的随机搜索更具有优越性,它可以避免其他优化算法(如蚁群算法、遗传算法)容易陷入局部最优的缺点,另外混沌优化算法具有较强的鲁棒性,易于其他算法融合,从而提高算法的优化性能。因此,COA-EO模型利用COA全局搜索能力强、能够快速逼近最优解的特点,弥补了EO算法容易陷入局部最优的不足;同时EO算法利用其强大的局部搜索能力,可以协助COA跳出局部极值,避免了COA过早成熟收敛。
2.2 混沌优化算法
混沌是一种似无规则、似随机的现象,并不是出于混乱状态,而是有着精致的内在结构。混沌是非线性动力学系统在一定形式下演变出来的运动形式,是系统在非平衡过程中产生的随机行为[18]。混沌变量在搜索优化时最常用的模型是Logistic模型,其方程为

式中λ∈[0,4]为控制参数,当λ取值为4时,系统处于完全混沌状态。
假设所求优化问题的描述如下:
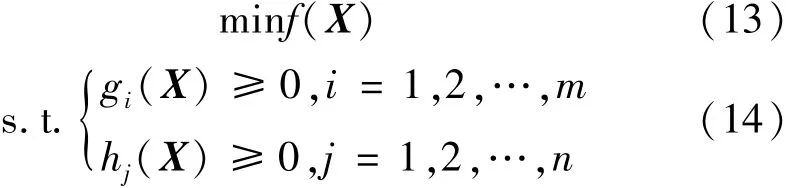
式中:f(X)为目标函数;gi(X)和hj(X)为约束函数。混沌优化算法在求解最优化问题时的步骤描述如下。
(1)初始化。设定控制误差ε,给定初始混沌向量x0,令k=0。
(2)将混沌变量映射到xk+1=λxk(1-xk),初始时,k=0,则x1=4x0(1-x0),令x∗=x1,f∗=f1。
(3)利用混沌变量进行迭代搜索,得出xk+1和fk+1,若|fk+1-fk|<ε,则x∗=xk,f∗=fk,结束,否则,转向步骤(4)。
(4)令k=k+1,转向步骤(3)继续循环。
2.3 混沌优化算法
混合COA-EO算法的目的是将二者的优势互补,从而避免了单个算法容易陷入局部最优、收敛速度慢等问题。但是,当EO算法加入到COA算法时,会增加计算的时间,减弱了原有算法的快速收敛能力,本文设定每隔Q代才将EO加入到COA算法中去,这样既保证了算法的快速收敛能力,同时又能跳出局部最优。变异算子对EO算法的性能起到至关重要的作用,因此本文采用自适应Lévy变异作为变异算子,Lévy函数的概率分布如式(14)所示:
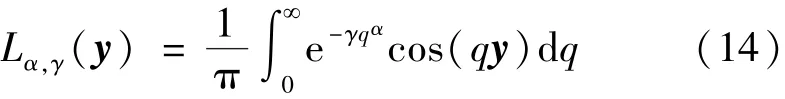
式中:γ为规模因子,且γ>0;参数α满足0<α< 2,当且仅当α=1时,分布函数为柯西概率分布;当α→2时,该分布接近于高斯概率分布。
综上,混合COA-EO算法的流程如下所示。
(1)初始化,设定控制误差ε,给定初始混沌向量x0,令χiteration=0。
(2)将混沌变量映射到xk+1=λxk(1-xk),初始时,k=0,则x1=4x0(1-x0),令x∗=x1,f∗=f1。
(3)利用混沌变量进行迭代搜索,得出xk+1和fk+1,若fk+1 (4)如果χiterationmod Q=0,则转向EO子程序,否则继续下一步。 (5)令χiteration=χiteration+1,若fk+1-fk<ε,结束,否则转向步骤(3)继续循环。 采用上述COA-EO算法对某地区配电网进行分布式电源选址、定容以及配电网规划。如图1所示,初始网络有8个节点、8条支路,现扩展成18个节点、24条支路的网络,除17、18节点不能用于连接分布式电源外,其余节点均可连接。图1中实线为已建线路,虚线为待建线路;节点相关数据如表1所示,新增负荷为15.6 MVA,分布式电源最大装机容量为: ZP=15.6×20%=3.12 MVA。线路部分数据如表2所示。 图1 初始配电网网络结构图Fig.1 Network structure of initial distribution network 表1 网络节点相关数据Table 1 Network node data 假设各个线路的年最大负荷利用小时数为Tmax=2000 h,单位电价为Cpu=0.5元/(kW·h);cDG=1.15元/(kW·h),cb=1元/(kW·h),规划年限为10 a;另外,由表1可知,规划水平年将新增负荷容量15.6 MVA,本文假设除配电站节点17、18之外,其他负荷节点均可安装DG。线路和分布式电源的年平均费用系数分别为q1=0.05、q2=0.35;风力发电的基本参数为:形状参数K=8.5,尺度参数C=2.0,风机切入风速vci=5 m/s,风机额定风速为vr=8 m/s,风机容量投资为7 200元/kW;太阳能光伏发电的基本参数为:形状参数α=0.85、β=0.8,光伏发电投资成本为27 000元/kW。 表2 线路部分参数及建设费用数据Table 2 Part of line parameters and construction cost data 采用MATLAB语言对COA-EO算法进行编程,求解目标函数并得到优化结果,为了能够对所得优化结果进行比较,本文同样利用COA-EO算法对不含DG的配电网进行规划。图2为含DG和不含DG配电网规划的Pareto前沿。 图2 COA-EO算法的Pareto前沿Fig.2 Pareto frontier of COA-EO algorithm 由图2可以看出,无论含有DG还是不含有DG的配电网网架优化,在低线损、低费用以及高DG容量区域并不存在解,这是因为在这些区域没有满足条件的解。DG的增加,使得所解决的问题更加复杂,但处于同一投资费用的情况下,含DG的线损要比不含DG的线损少很多,这也正是配电网需要引入DG的原因。 利用COA-EO算法优化所得的含DG的配电网网架结果如图3所示,不含DG的配电网网架结果如图4所示。 图3 含有DG的配电网网架优化结果Fig.3 Distribution network optimization results with DG 图4 不含DG的配电网网架优化结果Fig.4 Distribution network optimization results without DG 由图3可知,经过COA-EO优化所得的含DG的配电网拥有8条新建线路:line7-8,line7-18,line9-17,line9-10,line9-13,line11-12,line13-14,line15-16。 由图4可知,不含DG的配电网拥有12条新建线路:line4-8,line6-7,line7-8,line8-12,line9-13,line9-10,line9-17,line10-11,line11-12,line13-14,line14-15,line15-16。 表3为DG的位置和容量的优化结果。DG位置的选择相对容易一些,因为在不同的负荷节点均能够安装DG;然而DG容量的确定却不是很容易,负荷节点大小的不同使得安装的DG容量有大有小,只能根据具体的节点具体分析。由表3可知,分布式电源的安装总容量为3.1 MVA,其中风电安装容量为2.9 MVA,DG安装位置为节点4、6、7、8、10、11、12、13;光伏安装容量为0.2 MVA,DG安装位置为节点、14、15。 表3 DG的位置和容量优化结果Table 3 DG's position and capacity optimization results 将含有DG和不含有DG的配电网规划结果进行比较,结果如表4所示。由表4可知,含有DG的线路年投资费用为127万$,比不含DG的线路投资费用(169万$)要节省42万$;尽管DG的建设需要花费掉43.6万$,但含DG的损耗(45.7万$)要低于不含有DG的损耗(60.62万$),这也正是配电网规划引入DG的原因。进一步从综合费用来看,含有DG的综合投资要远远低于不含有DG的综合投资;因此,在配电网规划中引入DG,降低了网络损耗,提高了供电可靠性,并且降低了投资成本。 表4 2种不同方案的比较Table 4 Comparison between two different schemes万$ 为方便比较,本文还利用普通EO算法、GA算法以及ACO算法对上述案例进行计算规划,各个算法的迭代情况如图5所示,计算结果见表5。 由表5中数据可知,COA-EO算法计算所得的线路投资费用、DG安装费用、损耗费用分别为127.0万$,43.6万$,45.7万$,其优化效果要远远优于普通EO算法计算所得的136万$、53.7万$、49.6万$,这说明COA-EO算法跳出了局部最优,使得算法能够找到全局最优值,因此COA-EO算法的综合费用(216.3万$)要远远优于普通EO算法的综合费用(234.3万$)。GA算法计算结果稍优于ACO算法的计算结果,总体上相差不大,说明2种算法的性能相当;但这2种算法的计算结果要优于普通EO算法,说明这2种算法能够跳出局部最优,从而寻找出全局最优值。从表5中数据可知,本文提出的COAEO算法结合了COA算法和EO算法的优点,避免各自的缺陷,从而提高了算法的优化性能,所得计算结果优于表中其他3种优化算法,这也证明了本文所提出的COA-EO算法强大的搜索能力和优化能力,证明其具有有效性和可行性。 如图5所示,普通EO算法的迭代次数为17次,所对应的最优解为234.3万$,说明算法能够快速收敛并找到最优解,但EO算法与其他算法相比,明显地陷入了局部最优,并没有得到全局最优解。GA算法和ACO算法的迭代次数分别为31和34,所对应的最优解分别为226.90万$和228.36万$,说明GA算法的优化性能稍优于ACO算法。ACO-EO算法和GA-EO算法的迭代次数分别为30和33,所对应的最优解分别为223.59万$和220.73万$,说明通过融合,GA-EO算法虽然能够找到更优解,但其收敛速度却稍慢于ACO-EO算法;另外,GA-EO算法和ACO-EO算法的优化结果均优于单个EO、GA、ACO算法。COA-EO算法的迭代次数为26,所对应的最优值为216.3万$;说明COA-EO算法的收敛速度虽然低于普通EO算法,但其跳出了局部最优,避免了单纯EO算法的早熟现象,并且得到了全局最优结果;COA-EO算法的收敛速度要快于GA算法和ACO算法,说明COA-EO算法能够快速地逼近最优解,所得最优解优于GA和ACO的最优解。COAEO算法的迭代次数要低于ACO-EO算法和GA-EO算法,说明COA-EO算法的收敛速度快,能够快速逼近最优解;另外,COA-EO算法所得最优值优于ACO-EO算法和GA-EO算法,说明COA-EO的全局搜索能力更强,优化效果更佳。上述案例证明了COA-EO算法能够利用COA强大的搜索能力和EO算法的快速收敛能力,将二者的优势互补,避免各自的缺陷,在考虑分布式能源的配电网规划的应用中发挥了强大的优化性能,同时也证明了所提算法的有效性和可行性。 图5 各种算法的迭代图Fig.5 Iteration figures of different algorithms 表5 不同算法的优化结果比较Table 5 Optimization results comparison of different algorithms万$ 为了解决智能配电网发展背景下含DG的配电网规划问题,本文提出了基于混沌优化算法和极值动力学优化算法相互结合的多目标问题求解模型。首先,本文建立了以基于投资费用、损耗费用以及分布式电源容量的配电网规划目标函数,并介绍了分布式电源功率输出的计算方式和Pareto最优解的相关定义;其次,本文根据所建立的目标函数,将EO算法和COA算法相互融合,建立了COA-EO优化模型,并详细介绍了COA-EO算法解决配电网规划目标函数的流程和步骤;最后,本文将所建立的COA-EO算法应用于某地区的计及分布式电源的配电网规划。通过算例验证,结果表明COA-EO优化算法同时利用COA算法和EO算法的优点,从而成功避免了各自缺陷,使得普通EO算法跳出局部最优,避免了算法的早熟现象,从而得到了全局最优结果。另外,为得到更好的多目标优化结果,本文引入Pareto最优解,并利用所提出的COA-EO算法求解Pareto最优解。计算结果亦表明COA-EO算法的优化性能优于EO算法、GA算法和ACO算法,说明COA-EO算法是解决计及分布式电源配电网规划问题的有效工具。 虽然本文提出的COA-EO算法能够有效地解决计及分布式电源配电网规划问题,但算法在优化性能方面仍然具有较大的提升空间。例如,若将改进后的COA算法和EO算法融合,是否会提高算法的性能,能否成功地应用于电力系统多目标规划问题中等等;再者本文所提算法并没有应用于单目标优化问题,若应用,能否在解决配电网单目标规划问题时取得较好的效果,是否优于其他模型等,都是今后研究工作的主要方向。 [1]努尔·白克力.进一步提升配电网发展水平[N].中国能源报,2015-09-06:17. Noor·Bekri.Further promoting the development of distribution network[N].China Energy News,2015-09-06:17. [2]尤毅,刘东,于文鹏.主动配电网技术及其进展[J].电力系统自动化,2012,36(5):9-25. You Yi,Liu Dong,Yu Wenpeng.Technology and its trends of active distribution network[J].Automation of Electric Power Systems,2012,36(5):9-25. [3]张节潭,程浩忠,姚良忠.主动管理在含有分布式电源的配电网中的应用[J].电力科学与技术学报,2008,23(1):18-24. Zhang Jietan,Cheng Haozhong,Yao Liangzhong,Application of active management to distribution network with distributed generation [J].Power and Technology Science,2008,23(1):18-24. [4]Martine V F,Borges C L T.Active distribution network integrated planning incorporating distributed generation and load response uncertainties[J].IEEE Transactions on Power System,2011,26(4): 2164-2172. [5]杨新法,苏剑,吕志鹏,等.微电网技术综述[J].中国电机工程学报,2014,34(1):57-70. Yang Xinfa,Su Jian,Lyu Zhipeng,et al.Overview on Micro-grid Technology[J].Proceedings of the CSEE,2014,34(1):57-70. [6]Li D Q,Xu J Z,Luo Y.Distribution network expansion planning including distributed generation[C]//Proceedings of the CSUEPSA.Tianjin,China,2012,24(5):88-92. [7]Popovicz N,Kerleta V D,Popovic D S.Hybrid simulated annealing and mixed integer linear programming algorithm for optimal planning of radial distribution networks with distributed generation[J]. Electric Power Systems Research,2014(108):211-222. [8]Zhang H,Vittal V,Heydt G T,et al.A mixed-integer linear programmingapproachformulti-stagesecurity-constrained transmission expansion planning[J].IEEE Transactions on Power Systems,2012,27(2):1125-1133. [9]Paiva P C,Khodr H M,Domínguez-Navarro J A,et al.Integral planning of primary-secondary distribution systems using mixed integer linear programming[J].IEEE Transactions on Power Systems,2005,20(2):1134-1143. [10]Foster J D,Berry A M,Boland N,et al.Comparison of mixedinteger programming and genetic algorithm methods for distributed generation planning[J].IEEE Transactions on Power Systems,2014,29(2):833-843. [11]AlRashidi M R,AlHajriMF.Optimalplanningofmultiple distributed generation sources in distribution networks:A new approach[J].Energy Conversion and Management,2011,52(11): 3301-3308. [12]Abu-Mouti F S,El-Hawary M E.Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm[J].IEEE Transactions on Power Delivery,2011,26(4): 2090-2101. [13]Hung D Q,MithulananthanN.Multipledistributedgenerator placement in primary distribution networks for loss reduction[J]. IEEE TransactionsonIndustrialElectronics,2013,60(4): 1700-1708. [14]Paliwal P,Patidar N P,Nema R K.Planning of grid integrated distributed generators:A review of technology,objectives and techniques[J].Renewable and Sustainable Energy Reviews,2014 (40):557-570. [15]杨毅,韦钢,周冰.含分布式电源的配电网模糊优化规划[J].电力系统自动化,2012,36(5):9-25. Yang Yi,Wei Gang,Zhou Bing.Optimized fuzzy planning of the distributionnetworkincludingdistributedgeneration[J]. Automation of Electric Power Systems,2012,36(5):9-25. [16]王一,程浩忠.计及输电阻塞的帕累托最优多目标电网规划[J].中国电机工程学报,2008,28(13):13-15. Wang Yi,Cheng Haozhong.Pareto optimality based on multiobjective transmission planning considering transmission congestion [J].Proceedings of the CSEE,2008,28(13):13-15. [17]付晓刚,于金寿.基于极值动力学机制和信息融合搜索的混合算法及其应用[J].化工学报,2011,62(8):24-26. Fu Xiaogang,Yu Jinshou.A hybrid algorithm based on extremal optimization with adaptive levymutation and information fashion algorithm and its applications[J].Chemical Technology,2011,62 (8):24-26. [18]袁晓芳,王耀南.基于混沌优化算法的支持向量机参数选取方法[J].控制与决策,2006,21(1):13-16. Yuan Xiaofang,Wang Yaonan.Selection of SVM parameters using chaos optimization algorithmst[J].Control and Decision,2006,21 (1):13-16. (编辑:张媛媛) Pareto Optimal Planning Model of Distribution Network with DG Based on COA-EO Hybrid Algorithm ZENG Ming,PENG Lilin,FAN Qiannan,LI Ran Distribution network planning with DG is a complex combinatorial optimization problem.Along with the development of smart distribution network and fluctuant renewable energy access,it puts forward higher requirements on the efficiency of optimization model.This paper proposed COA-EO algorithm which combined chaos optimization algorithm (COA)and extreme dynamics optimization algorithm(EO)to solve the multi-objective optimization problem.The example verification results show that COA-EO optimization algorithm can take advantage of both COA and EO and manage to avoid the shortcomings,so that it can make ordinary EO escape from local optimal solution,avoid the premature phenomenon of the algorithm,and eventually obtain the globally optimal solution.In addition,in order to get a better multi-objective optimizationresult,this paper introduced the Pareto optimal solution,and used the proposed COA-EO algorithm to solve the Pareto optimal solution.The calculation results show that the optimization performance of COA-EO algorithm is superior to EO,genetic algorithm(GA),ant colony optimization(ACO),ACO-EO algorithm and GA-EO algorithm,which indicates that COA-EO algorithm is effective for distribution network planning with DG. distribution network planning;distributed generation;renewable energy;COA-EO hybrid optimization algorithm;Pareto optimal solution TM 715 A 1000-7229(2015)11-0001-09 10.3969/j.issn.1000-7229.2015.11.001 2015-08-04 2015-10-27 曾鸣(1957),男,教授,博士生导师,从事电力系统规划、需求侧管理、电力市场与技术经济研究工作; 彭丽霖(1991),女,博士研究生,研究方向为电力系统规划、电力技术经济分析等; 樊倩男(1994),女,硕士研究生,研究方向为电力技术经济分析等; 李冉(1992),女,硕士研究生,研究方向为电力技术经济分析等。 国家自然科学基金项目(51277067,71271082);中央高校基本科研业务费专项资金资助(2015XS37);国家软科学研究计划项目(2012GXS4B064)。 Project Supported by National Natural Science Foundation of China(51277067,71271082);The Fundamental Research Funds for the Central Universities (2015XS37);National Soft Science Research Project(2012GXS4B064)。3 算例分析
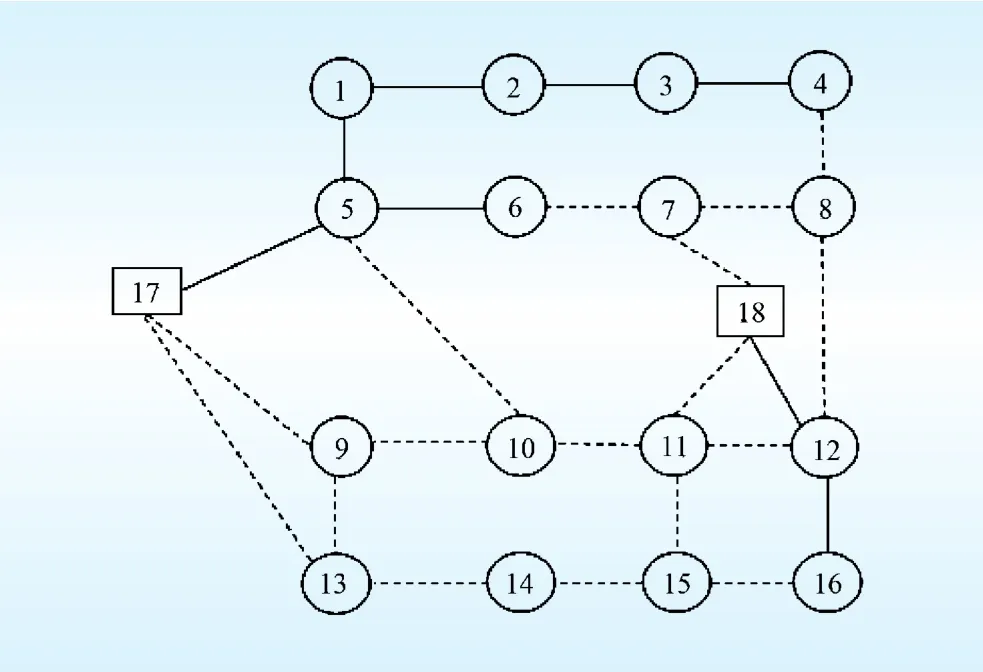

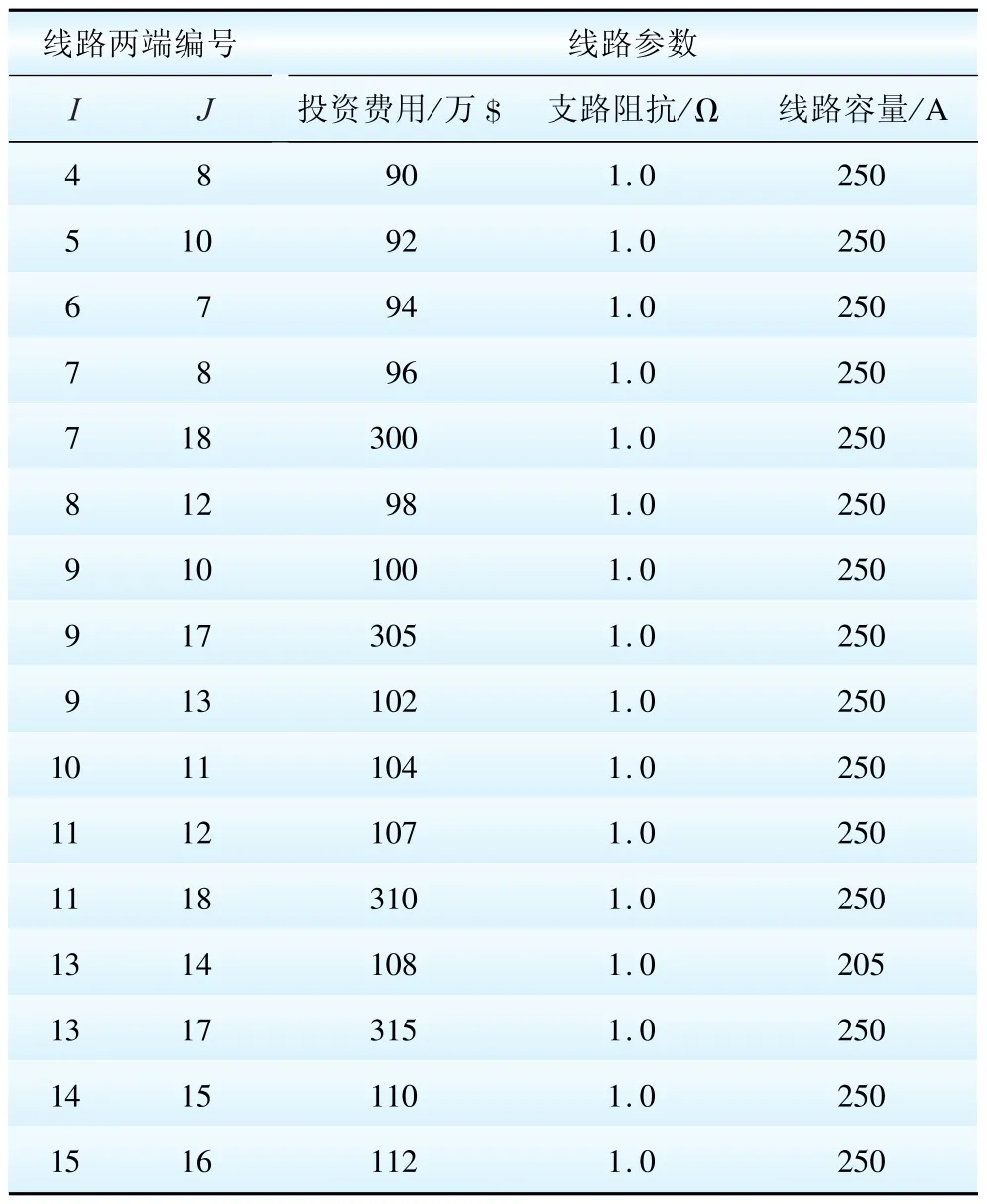
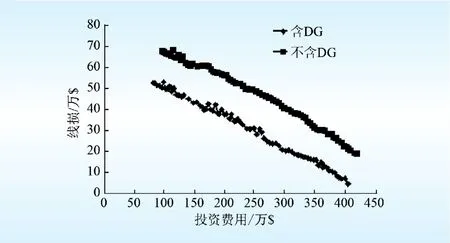

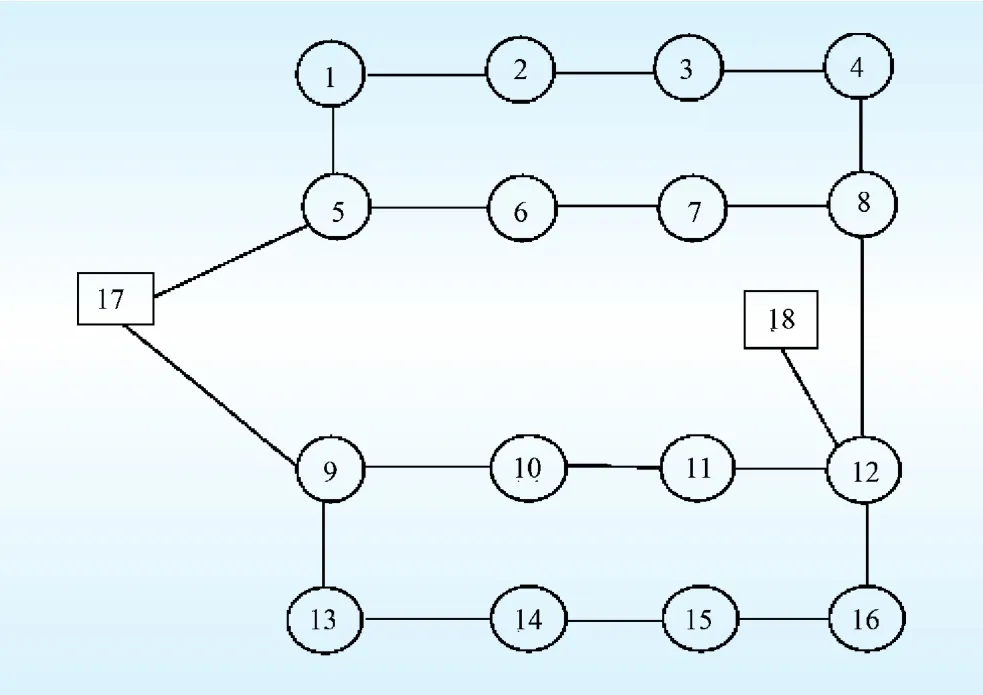



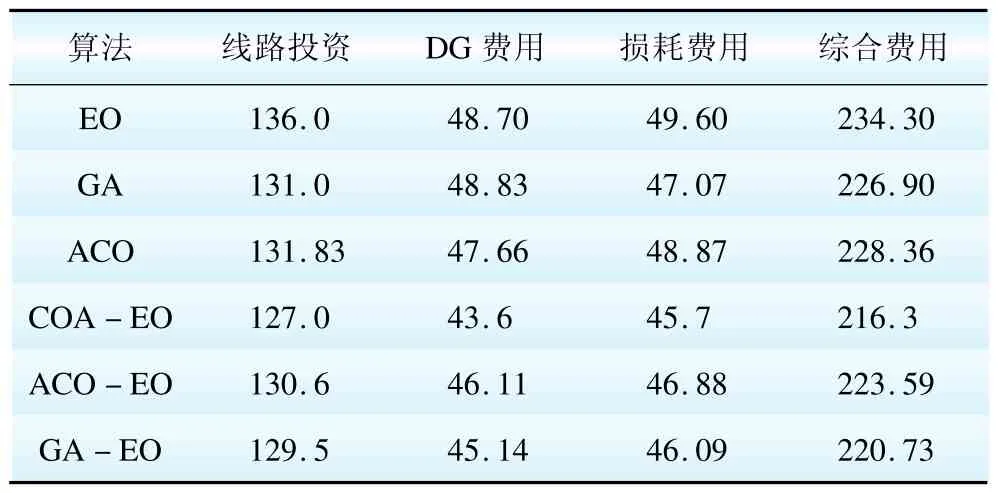
4 结 论
(School of Economics and Management,North China Electric Power University,Beijing 102206,China)
