基于NSGPBB算法的压缩感知稀疏信号重构

郭 晓,李向利

基于NSGPBB算法的压缩感知稀疏信号重构

郭 晓,李向利

(桂林电子科技大学数学与计算科学学院,广西桂林 541004)

为了更好地重构原始信号,提出一种带有交替BB步长的非单调梯度投影算法(NSGPBB)。将无约束凸优化问题转化为在闭凸集上的边界约束二次规划问题,并证明了该算法的收敛性。数值实验结果表明,该算法是有效的,且收敛速度快于梯度投影算法。

压缩感知;谱梯度投影算法;稀疏重构;二次规划;交替BB步长

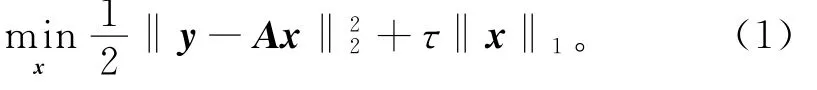
其中:x∈Rn为原始信号,在正交基下可稀疏或可压缩;y∈Rm为低维测量向量;τ为非负参数;‖x‖1=

在压缩感知[1]中,一般考虑无约束凸优化问题:为L 1范数;‖·‖2为Euclidean范数;A为m ×n(m≪n)感知矩阵,A=ΦΨ,随机观测矩阵Φ为m ×n随机高斯矩阵,Ψ为n×n正交变换基矩阵。当y包含噪声或x仅仅可压缩但不精确稀疏时,测量向量y=Ax+ζ,ζ为高斯白噪声。在一定条件下,式(1)可等价于以下2个凸约束优化问题:

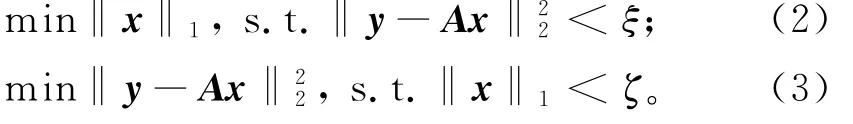
其中ξ、ζ为非负实参数。式(2)为二次约束线性规划问题,式(3)为二次规划问题。

为了求解以上优化问题,近年来学者们提出了许多相关算法,如稀疏重构梯度投影(GPSR)算法[2],内点(IP)算法[3],迭代压缩/阈值化(IST)算法[4],同伦(HM)算法[5]以及加权最小L1范数法[6]等。在信号处理中,这些算法都能有效地恢复信号。

谱梯度投影(SPG)算法[7]是求解边界约束优化问题的有效方法,并已应用于问题(3)。文献[8]提出了一种求解无约束优化问题的非单调Wolfe线搜索算法,该算法具有较好的数值效果。文献[9]利用文献[8]中的非单调Wolfe线搜索给出了求解边界约束优化问题的梯度投影(NSPG)算法。文献[10]证明了交替使用BB步长[11]比单独使用某一个BB步长的数值效果更好。鉴于此,结合非单调Wolfe线搜索和交替BB步长,提出一种新的梯度投影算法,并将该算法应用到恢复稀疏信号中。

1 压缩感知信号重构模型与算法

1.1 边界约束二次规划(BCQP)模型

受文献[12]的启发,为了更方便地求解问题(1),将其转化为一个闭凸集上的二次规划问题。将向量x分解为正负2部分,即x=u-v,u≥0,v≥0。向量u,v分别满足ui=(xi)+,v=(-xi)+,i=1,2,…,n。操作符(·)+定义为(xi)+=max{0,xi}。‖x‖1=1Tnu+1Tnv。其中1Tn=[1,1,…,1]T为长度为n的1向量,因此,式(1)可写成BCQP问题:

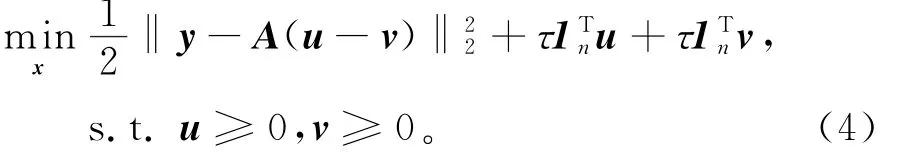
若令u←u+θ,v←v+θ,其中θ≥0为转换向量,式(1)中L1范数项的值不变,因此,式(4)可写成标准的BCQP问题:

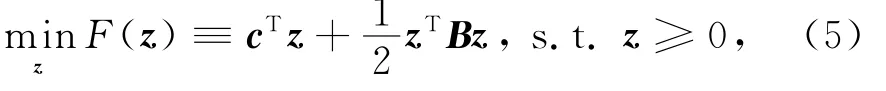
其中:

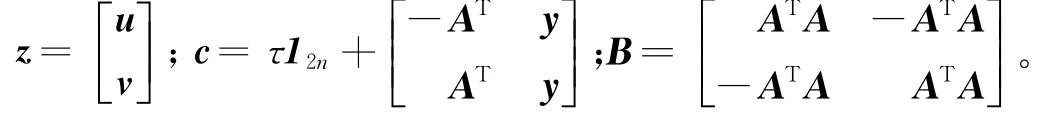
问题(5)可看作带凸集约束的非线性规划问题:

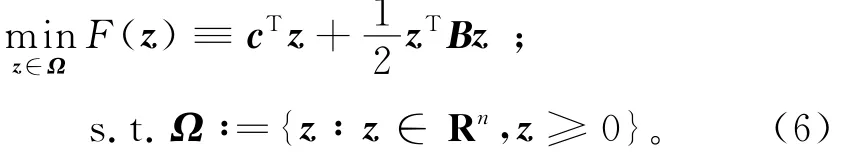
其中:

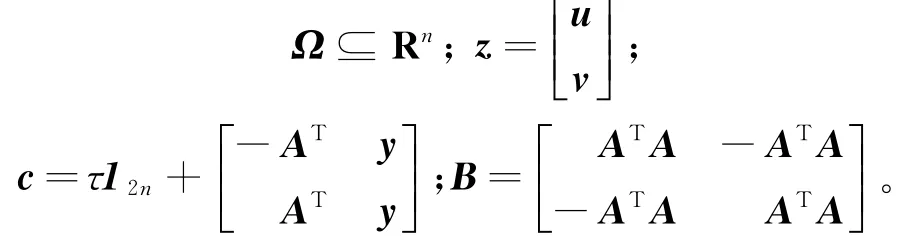
因此,可将重构压缩感知稀疏信号问题(1)直接转换为求解问题(6)。

1.2 非单调梯度投影算法

带凸集约束非线性规划问题的一般性GLP(goldstein-lavitin-polyak,简称GLP)梯度投影算法[9],其迭代公式为:

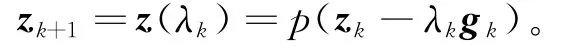
其中:投影算子p(·):Rn→Ω定义为

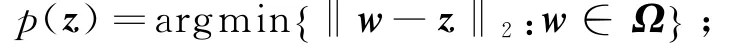
gk为F(z)在zk点的梯度,且在Ω上是Lipschitz连续的;λk为满足广义Armijo线性搜索条件的步长。

Zhang等[8]根据如下非单调Wolfe线搜索选择步长λk:

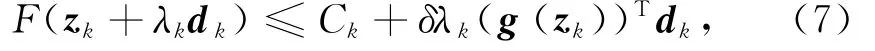
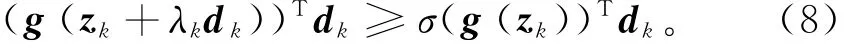
其中:dk为搜索方向;0＜δ＜σ＜1。给定Q0=1, C0=F(z0),ηk∈[0,1]为给定常数,则

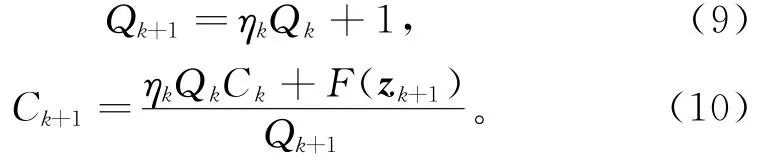
结合非单调线搜索(7)和交替BB步长,求解问题(6)的NSGPBB算法步骤为:

1)初始化。z0∈Ω,0＜σ1＜σ2＜1,0＜αmin＜α0＜αmax＜∞,δ∈(0,1),C0=F(z0),Q0=1, k∶=0。

2)计算dk=p(zk-αkgk)-zk,λ=1。

3)令z+=zk+λkdk。

4)若

则令λk=λ,zk+1=zk+λkdk,sk=zk+1-zk,lk=gk+1-gk,转步骤5);否则λk=σλk,σ∈[σ1,σ2],转步骤3)。

5)若满足停止准则,则算法停止,否则由式(9)、(10)计算Qk+1、Ck+1,并令k=k+1。

步骤2)中的αk选择算法:

a)若k=0,则令τ1∈(0,1)并给定非负整数M。

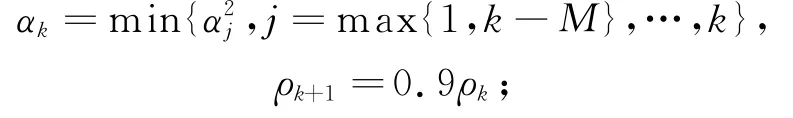
否则,αk=α1k,ρk+1=1.1ρk。

2 算法的收敛性分析

为了分析算法的收敛性,定义

gα(z)=p(z-αg(z))-z,α∈[αmin,αmax]。若z为约束稳定点,由文献[13]可知,gα(z)=0,即‖dk‖=0。若〈g(zk),dk〉≤0,由文献[8]中的引理知,F(zk)≤Ck。

引理1[10]对z∈Ω,有

引理2 若λk满足式(10),则对所有的k＞0,

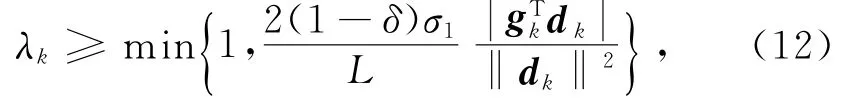
其中L为g(z)的Lipschitz常数。

证明 若λk=1满足式(10),则式(11)成立,否

则,存在σ∈[σ1,σ2],使得不满足式(12),即

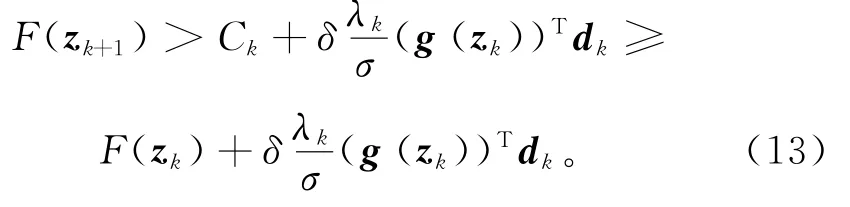
另一方面,

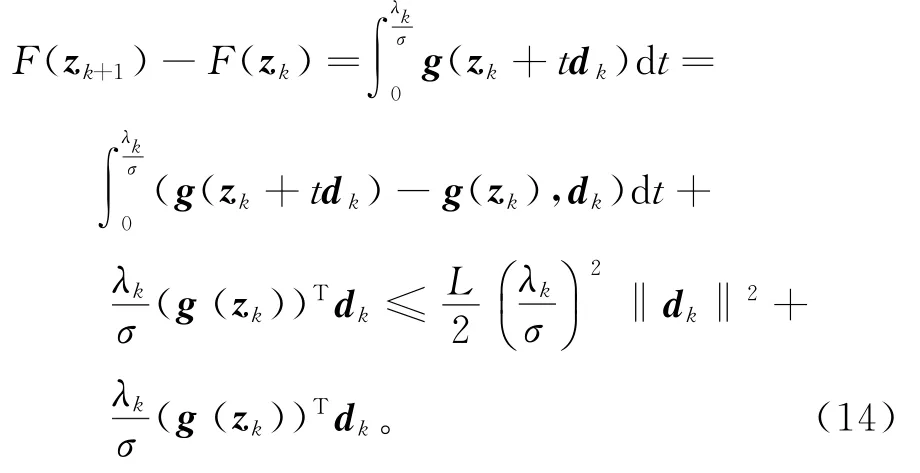
由不等式(13)、(14)可得

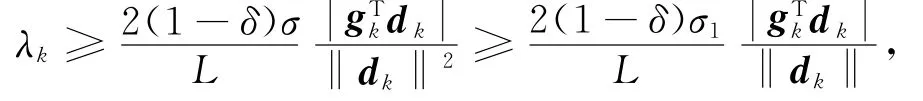
故式(12)得证。

引理3[9]若序列{zk}由NSGPBB算法产生,则

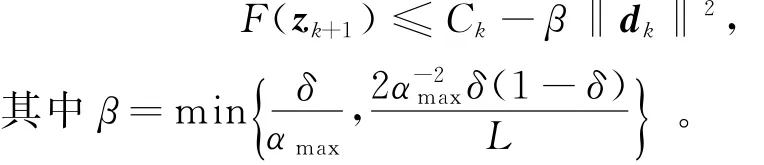
定理1 若序列{zk}由NSGPBB算法产生,则{zk}的每个极限点均为问题(6)的约束稳定点。

证明(反证法) 假设{zk}的极限点z-不是约束稳定点,则‖dk‖＞η,η为一个很小的正数。由引理1,对所有的k＞0,有＜-ε,ε＞0。

由式(10)和引理3可知:

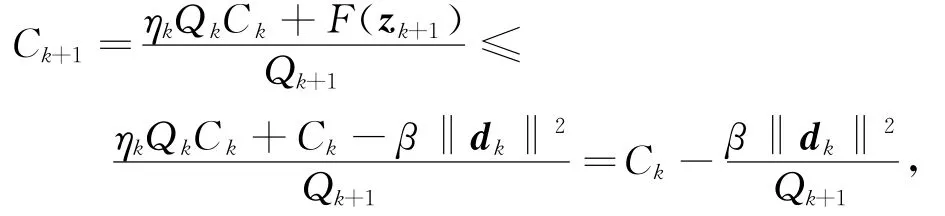
则有

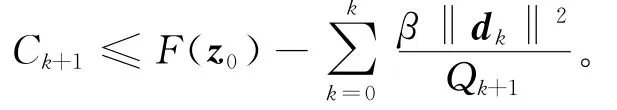
由式(9)和ηk∈[0,1]得

由式(11)可直接推出:

由引理1、2可知:

则

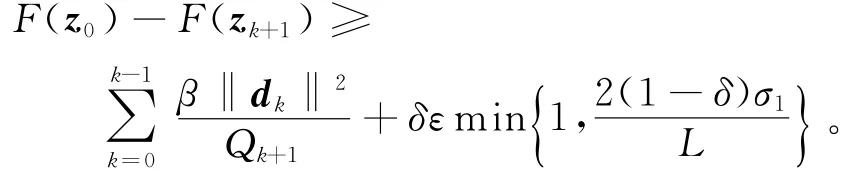
又因为

故

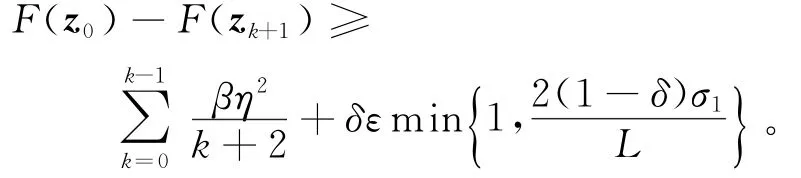
由F(zk)有下界可知,F(z0)-F(zk+1)＜∞,而当k→∞时,有F(z0)-F(zk+1)→∞,矛盾,即

因此定理成立。

3 数值试验

为了验证该算法恢复原始信号的有效性,将NSPGBB算法与SPG算法[7]、修正谱共轭梯度投影(SCG)算法[14]、NSPG算法[9]进行数值实验比较。数值实验运行环境:硬件为2 GHz处理器、2 GB内存的笔记本电脑,软件为Matlab7.12(R2011a)。实验数据设置:原始信号x的长度为n=4096,A为m× n高斯随机矩阵,观测向量y的长度为m=1024,x中包含160个随机±1元素。参数初始化:噪声参数ζ= 0.01,τ=0.08‖ATy‖∞,任意向量a的无穷范数定义为‖a‖∞=max|ai|,i=1,2,…,n,η=0.80,αmin=10-10,αmax=1010,ρ1=0.5,σ=0.5,δ=0.25,M= 2。用最小均方误差E评价重构信号的质量:

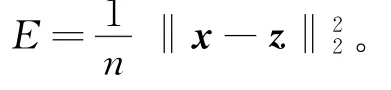
其中:x为原始信号;z为恢复信号。E值越小,信号重构的质量越高。算法的终止条件为:

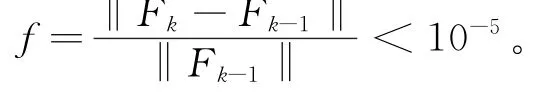
图1为4种算法的信号恢复效果,图2为4种算法的收敛曲线。从图1可看出,4种算法均能很好地恢复含有噪声的信号。分别从运行时间、迭代步数和最小均方误差3项指标比较4种算法的性能,算法的数值结果如表1所示。从表1可看出,4种算法恢复信号的质量相似,即E值相差不大,但NSPGBB算法无论在迭代步数还是CPU运行时间上都比其他3种算法更有优势,这表明NSPGBB算法能更快地恢复原始信号。图2的收敛曲线进一步验证了这个结论。

图1 4种算法的信号恢复效果Fig.1 Recovery effect of four algorithms

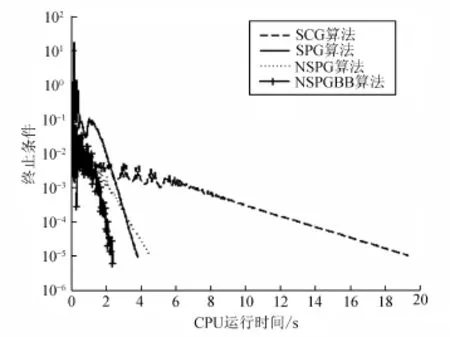
图2 4种算法的收敛曲线Fig.2 Convergence curve of four algorithms

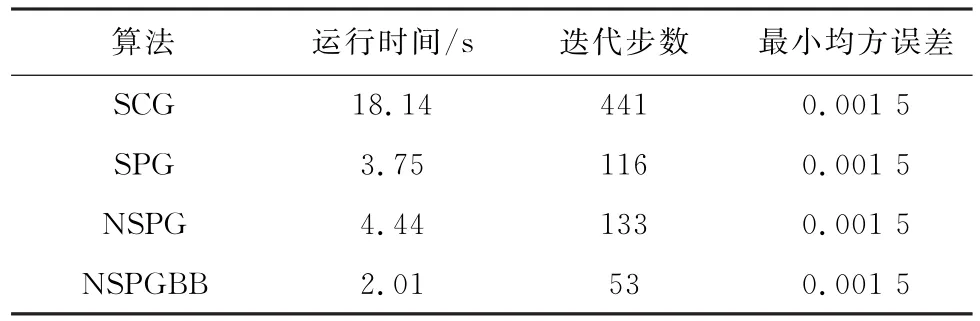
表1 4种算法的数值结果Tab.1 Numerical results of four algorithms

4 结束语

针对大规模稀疏信号的重构问题,结合非单调Wolfe线搜索和交替BB步长,提出了一种交替BB步长非单调梯度投影算法,并证明了该算法是全局收敛的。与梯度投影算法相比,该算法的优点在于交替使用BB步长加快了线性搜索。数值实验结果表明,该算法能够有效地恢复原始信号,且与其他谱梯度投影算法相比,收敛速度更快。

[1] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[2] Figueiredo M A T,Nowak R D,Wright S J.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing,2007,1 (4):586-597.

[3] Kim S J,Koh K,Lustig M,et al.An efficient method for compressed sensing[C]//IEEE International Conference on Image Processing,2007:117-120.

[4] Elad M.Why simple shrinkage is still relevant for redundant representations[J].IEEE Transactions on Information Theory,2006,52(12):5559-5569.

[5] Malioutov D M,Cetin M,Willsky A S.Homotopy continuation for sparse signal representation[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing,2005:733-736.

[6] Candes E,Braun N,Wakin M.Sparse signal and image recovery from compressive samples[C]//IEEE International Symposium on Biomedical Imaging:From Nano to Macro,2007:976-979.

[7] Birgin E G,Martínez J M,Raydan M.Nonmonotone spectral projected gradient methods on convex sets[J]. SIAM Journal on Optimization,2000,10(4):1196-1211.

[8] Zhang Hongchao,Hager W W.A nonmonotone line search technique and its application to unconstrained optimization[J].SIAM Journal on Optimization,2004,14 (4):1043-1056.

[9] 毕亚倩,刘新为.求解界约束优化的一种新的非单调谱投影梯度法[J].计算数学,2013,35(4):419-430.

[10] Frassoldati G,Zanni L,Zanghirati G.New adaptive stepsize selections in gradient methods[J].Journal of Industrial and Management Optimization,2008,4(2): 299-312.

[11] Barzilai J,Borwein J M.Two-point step size gradient methods[J].IMA Journal of Numerical Analysis, 1988,8(1):141-148.

[12] Calamai P H,MoréJ J.Projected gradient methods for linearly constrained problems[J].Mathematical Programming,1987,39(1):93-116.

[13] Bertsekas D P.Nonlinear Programming[M].Belmont: Athena Scientic,1995,239-240.

[14] Zhang Benxin,Zhu Zhibin.A modified spectral conjugate gradient projection algorithm for total variation image restoration[J].Applied Mathematics Letters, 2014,27:26-35.

编辑:张所滨

Compressed sensing sparse signal reconstruction based on NSGPBB algorithm

Guo Xiao,Li Xiangli
(School of Mathematics and Computational Science,Guilin University of Electronic Technology,Guilin 541004,China)

To solve a key problem of sparse signal reconstruction,a nonmonotone gradient projection algorithm with the alternation of Barzilai-Borwein rules(NSGPBB)is proposed for bound-constrainted quadratic programming(BCQP)on a convex set.Global convergence of this method is proved.The numerical results show that the method is effective and faster than other spectral gradient projection algorithms.

compressed sensing;spectral gradient projection;sparse reconstruction;quadratic programming;alternation of Barzilai-Borwein rules

O224

A

1673-808X(2015)05-0427-04

2015-06-05

广西自然科学基金(2014GXNSFAA118003);广西教育厅科研项目(ZD2014050)

李向利(1977-),女,陕西宝鸡人,副教授,博士,研究方向为最优化理论与算法。E-mail:lixiangli@guet.edu.cn

郭晓,李向利.基于NSGPBB算法的压缩感知稀疏信号重构[J].桂林电子科技大学学报,2015,35(5):427-430.