自适应人工蜂群优化的混沌系统参数估计*

任开军，邓科峰，刘少伟，宋君强(国防科技大学海洋科学与工程研究院，湖南长沙410073)

自适应人工蜂群优化的混沌系统参数估计*

任开军，邓科峰，刘少伟，宋君强
(国防科技大学海洋科学与工程研究院，湖南长沙410073)

为了对混沌系统未知参数进行准确估计，改进了人工蜂群优化算法，提出自适应人工蜂群算法的混沌系统参数估计方法。将混沌系统参数估计问题转化为多维变量数值优化问题，利用人工蜂群算法对未知参数进行导向随机搜索。在搜索过程中，通过种群优化程度和解的质量自适应地调整更新步长和解的尝试次数。以Lorenz混沌系统为例进行的仿真实验表明，该方法在无噪声和噪声强度较大的情况下均能够获得较好的估计结果，表现出较强的鲁棒性。

混沌系统；参数估计；人工蜂群；数值优化

自1963年Lorenz发现第一个混沌吸引子以来，学术界对混沌系统理论展开了深入的研究，提出的混沌控制与同步方法在保密通信、信息科学、化学反应以及生物医学等领域得到了广泛的应用［1］，并成为当前混沌系统与控制学科交叉研究的热点。在混沌系统中，参数未知的情况时常发生。例如，混沌系统的复杂性导致它的某些参数无法测量或确定；系统的保密性要求使得某些参数不可获知。由于现有的多数混沌同步与控制方法均是在系统参数已知的情况下获取的，所以其在参数未知的情况下不再适用。此时，对混沌系统的未知参数进行有效估计便成为混沌控制与同步方法研究的前提和关键。

群智能优化算法是解决混沌系统参数估计问题的一类重要方法［3-18］。不同于变分法基于导出的混沌系统伴随方程和待估计参数的泛函梯度公式单点搜索最优值［2］，群智能优化算法从一组随机解出发并通过模仿生物进化过程或群体智能过程来实现最优值的导向性搜索。例如，文献［3］采用的遗传算法与文献［4-5］提出的混合差分进化算法均属于基于生物进化机制的算法；而文献［6］提出的混合生物地理优化算法、文献［7-8］提出的混沌蚁群算法、文献［9-12］提出的量子粒子群算法则是基于群体智能过程的优化算法。由于群智能优化算法以一组可行解为初始值，采用结构化和随机化搜索策略，不需要目标函数的导数信息，对函数性质也没有太多要求，因此在求解高度非线性的混沌系统未知参数上相比于传统优化算法显示出较大的优势。

人工蜂群(Artificial Bee Colony，ABC)优化算法是由Karaboga在2005年提出的模仿蜜蜂采蜜行为的群智能优化算法［13-15］。与蚁群算法(Ant Colony Optimization，ACO)和粒子群算法(Particle Swarm Optimization，PSO)一样，ABC也是一种基于生物群体智能过程的优化算法。在ABC算法中，食物源代表着问题的解，食物源的食物越充足表示解的质量越好，而蜜蜂的采蜜行为则表示寻找最优解的过程。蜜蜂作为一种群居性动物，虽然单个个体的行为非常简单，但是群体却展现出极其复杂的行为。在采蜜过程中，采蜜的蜜蜂通过跳摇摆舞的方式将食物源信息反馈给其他蜜蜂，引导更多的蜜蜂放弃贫源到富源采蜜，从而实现问题解的不断优化。ABC算法提出后被成功应用在函数优化、组合优化、频谱分配等问题中［16-17］，具有设置参数少、计算简单、收敛速度快和鲁棒性高等特点。

任开军等将ABC算法引入到混沌系统的参数估计中，并将其与经典的ACO、PSO以及最近提出的生物地理学优化算法(Biogeography Based Optimization，BBO)［18］进行比较。由于基本ABC算法在参数估计过程容易丢弃最优解而导致算法性能波动很大，任开军等提出自适应人工蜂群(Adaptive Artificial Bee Colony，AABC)优化算法，利用自适应的食物源淘汰策略延长精英解的存活时间。

1 混沌系统参数估计问题

考虑具有m个参数的n维混沌系统，其状态变量的估计值为:

其中，X=(x1，x2，…，xn)T是原系统的n维状态变量，X0是系统初始状态，θ=(θ1，θ2，…，θm)T是系统参数的真实值。

假设系统结构已知，当对系统参数进行估计时，被估计系统可以描述为:

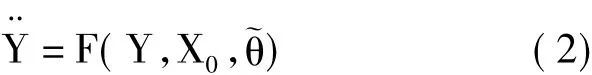
其中，Y=(y1，y2，…，yn)T∈Rn是被估计系统的n维状态变量，~θ=(~θ1，~θ2，…，~θm)T是系统参数的估计值。

假设在k时刻，真实系统和待估计系统的状态变量分别为Xk和Yk，~Xk为真实系统的测量噪声，M表示用于参数估计的系统状态变量序列长度，那么混沌系统参数估计问题则可以转化为最优化问题:

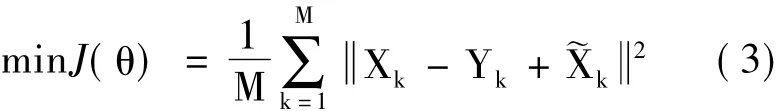
为了准确地辨识出混沌系统的未知参数，估计算法采用如图1所示的流程对估计值进行迭代求精。首先，利用原系统输出序列X1，X2，…，XM、测量噪声~X和待估计系统输出序列Y1，Y2，…，YM计算得到参数估计的误差平方和J(θ)；然后，将J(θ)反馈到估计算法中用于生成新的估计值；最后，通过不断地迭代，使得获取的估计值~θ能够将优化函数J最小化。引入ABC算法并提出自适应的AABC算法用于混沌系统的参数估计，并与其他群优化算法进行比较，以此验证ABC算法在混沌系统参数估计中的有效性。

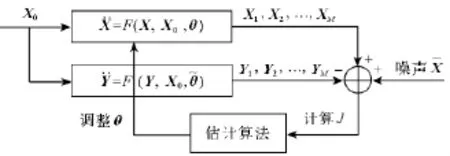
图1 混沌系统参数估计原理图Fig.1 Parameter estimation model for chaotic systems

2 自适应人工蜂群优化算法

在AABC算法中，存在着三种不同类型的蜜蜂:雇佣蜂、观察蜂和侦查蜂。蜂群中一半的蜜蜂为雇佣蜂，而另一半由观察蜂和侦查蜂组成。雇佣蜂负责从先前发现的食物源处将蜂蜜采集回蜂巢并将食物源质量信息传递给在蜂巢守候的观察蜂。在蜂巢等待的观察蜂根据雇佣蜂共享的食物源信息决定去哪一个食物源采蜜。侦查蜂则负责在蜂巢附近随机地或基于某些外部线索进行侦查以寻找新的食物源。在采蜜过程中，蜂群表现如下所示的群体智能行为:

1)在初始阶段，蜜蜂在蜂巢附近通过随机搜索寻找食物源。

2)在找到一个食物源后，该蜜蜂成为雇佣蜂并从发现的食物源处采集蜂蜜。在将蜂蜜采集回蜂巢后，雇佣蜂或直接或跳一段摇摆舞将食物源信息共享给其他蜜蜂后返回食物源。如果雇佣蜂对应的食物源开发殆尽，该雇佣蜂便成为侦查蜂并开始随机地搜索新的食物源。

3)观察蜂在蜂巢守候并通过观察雇佣蜂的摇摆舞获取食物源的相关信息，根据每个摇摆舞的发生频率(与食物源的质量成正比)选择一个高质量的食物源而成为采蜜的雇佣蜂。

2.1 初始化阶段

AABC算法初始时每个雇佣蜂随机生成一个食物源，每个食物源对应着解空间中的一组可行解，因此雇佣蜂的总数即为搜索空间的大小。初始解的生成公式为:

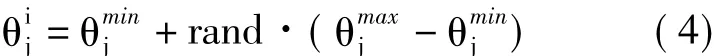
其中:i=1，2，…，n，n为雇佣蜂的数量；j=1，2，…，m，m为待估计的参数个数；rand为0～1的随机数；θmjin和θmjax分别表示第j个参数θj取值的上下界。此外，ABC算法加入了一个Trial(i)数组用于记录第i组解被尝试优化的次数，Trial数组初始时设置为0。系统初始化后，雇佣蜂、观察蜂和侦查蜂开始工作，表示AABC算法进入迭代搜索过程，当搜索达到最大搜索次数MaxGen时算法结束。

2.2 雇佣蜂阶段

每次迭代搜索时，雇佣蜂会修改记忆中的食物源位置，使得本次搜索的食物源邻近于上次获取的食物源。在AABC算法中，θi的邻域解定义为只改变θi中某个参数的解:

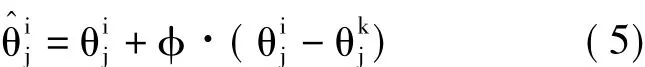
其中，j∈［1，m］为随机选择的第j个参数，θk为随机选择的不同于的第k组解，φ为［-1，1］的随机数。值得注意的是，如果，那么取值为；如果＜，那么θ取值为从式(5)可以看到，随着和之间差距的缩小，的摄动将减小，使得AABC算法中解的更新步长能够随着解空间的不断优化而自适应地缩短。的适应度为:

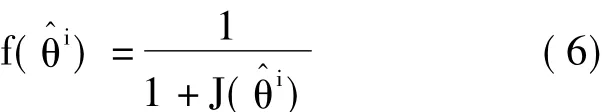
2.3 观察蜂阶段

在完成搜索后，雇佣蜂把食物源质量信息共享给在蜂巢等待的观察蜂。观察蜂收集到所有食物源的质量信息后，按照轮盘法选择一个食物源作为自身开采蜂蜜的地点:

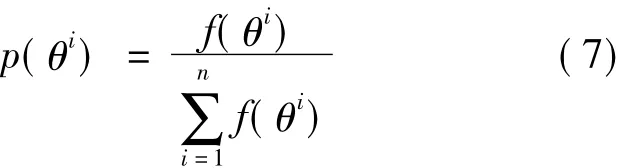
利用式(7)对食物源进行概率性选择，质量越高的食物源将吸引更多观察蜂前去开采，从而使得解空间能够更好地得到优化。具体地，AABC算法首先生成一个［0，1］的随机数r，如果r小于p(θi)，那么侦查蜂选择θi作为食物源；否则侦查蜂继续测试下一个食物源θi+1。在食物源选定后，该侦查蜂成为雇佣蜂并采用第2.2节所述的过程更新自身的食物源。

2.4 侦查蜂阶段

在雇佣蜂和观察蜂完成搜索后，AABC算法检查是否存在开发殆尽的食物源需要被淘汰。在先前雇佣蜂和观察蜂的搜索过程中，如果食物源θi持续不能获得更新，那么Trial(i)将一直增加。如果雇佣蜂和观察蜂阶段完成后Trial(i)超过食物源的最大利用程度limit，那么该食物源将被认为消耗完毕而遭到放弃。此时，与该食物源对应的雇佣蜂转变为侦查蜂而开始搜索新的食物源——用式(4)生成的随机解替换原始解。在基本ABC算法中，每次迭代仅有一个食物源被认为消耗殆尽而需要替换。因此，当多只雇佣蜂的Trial值超过limit时，具有最大Trial值的那只雇佣蜂被选择为侦查蜂。

基本ABC算法的问题在于高质量解由于较长时间不能得到优化，其Trial值将持续增加，从而在侦查蜂阶段很可能被选择抛弃掉。虽然基本ABC算法的初衷在于通过这种淘汰机制跳出局部最优解，但也导致精英解无法得到继承。因此，AABC算法利用目标函数值J(加权Trial(i):

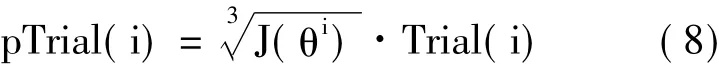
当pTrial(i)最大并且大于limit时，算法将放弃该食物源。采用式(8)的原因在于采用根号函数加权后，只有在连续limit次迭代得不到更新的情况下才会被抛弃，使得θi的开采次数与其质量成正比。值得注意的是，为了折中加权函数对高质量食物源和低质量食物源的开采，AABC算法选择三次根号作为加权函数。

3 数值仿真结果及分析

以典型的Lorenz混沌系统为例，说明引入的ABC算法和改进的AABC算法在混沌系统未知参数估计中的有效性。Lorenz系统的动力学方程为:

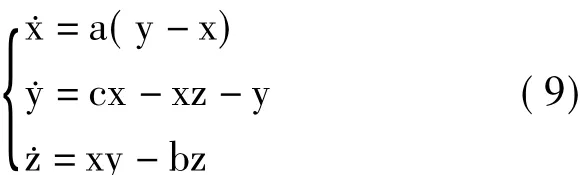
其中:x，y，z为系统状态变量；a，b，c为待估计的参数。特别地，在一个两平衡板间热对流的环流中，x表示流体速度，y和z分别表示水平方向和垂直方向上的温差；a和c分别与流体的Prandtl数和Rayleigh数成比例，b是流体空间水平和垂直方向的特征数。当参数a=10，b=8/3，c=28时，系统表现为混沌状态。数值仿真采用龙格-库塔算法求解式(9)，步长h=0.01。观测数据采集过程为:先让Lorenz系统自由演化，在经历暂态后任意选取一点作为0时刻，然后以此为起点连续演化至M步长时刻，得到M个状态变量值，仿真实验取M=300。

将基本ABC算法和改进的AABC算法与ACO算法、BBO算法以及PSO算法相比较。在所有算法中，种群大小n=50，迭代次数MaxGen= 100。ABC算法中limit设置为5；ACO算法中信息量Q=20，信息启发因子α=1，期望启发因子β=5，信息素全局残留系数ρg=0.9，局部残留系数ρ1=0.9；BBO算法中最大迁徙率E=I=1，最大变异率ρm=0.005；在PSO算法中惯性权重w=0.3，加速因子c1=c2=c3=1。Lorenz混沌系统各参数的搜索范围为:9≤a≤11，2≤b≤3和20≤c≤30；搜索精度为10-6。

表1给出了各算法在无噪声情况下独立执行20次后得到的最优值、最差值和平均值。优化函数J越小，估计精度越高。从表1中可以看到，基本ABC算法和改进的AABC算法在最优情况下具有类似的结果，在估计精度上这两种算法的最优值、最差值以及平均值都要优于其他算法。尤其是AABC算法，在最坏情况下仍然能够获得精度很高的估计值。在平均估计值上，ABC算法优于其他算法一个数量级，AABC算法优于基本ABC算法将近20倍。值得注意的是，虽然PSO算法最优值的估计精度最差，但是最差情况和平均情况下却具有较好的结果。

图2显示了所有算法在各自最优情况下目标函数J(θ)的迭代收敛曲线。由于基本ABC算法在解连续limit次不能提高时便抛弃该解，虽然这种机制有利于算法跳出局部最优解，却导致目标函数在迭代过程中剧烈波动。其他算法的收敛曲线则呈现出逐步下降的趋势。其中，PSO算法在前期具有最快的收敛速度，之后长时间陷入局部最优解；ACO算法和AABC算法在前期具有显著的收敛度，在后期收敛速度明显变慢；BBO算法具有较平稳的收敛速度。图3显示了待估计参数a，b，c的优化曲线。从图3中可以看到，PSO算法和AABC算法在10次迭代内即收敛到真实值附近，而ACO算法和BBO算法在20次左右收敛到真实值。整体而言，AABC算法具有更加优异的全局寻优能力。

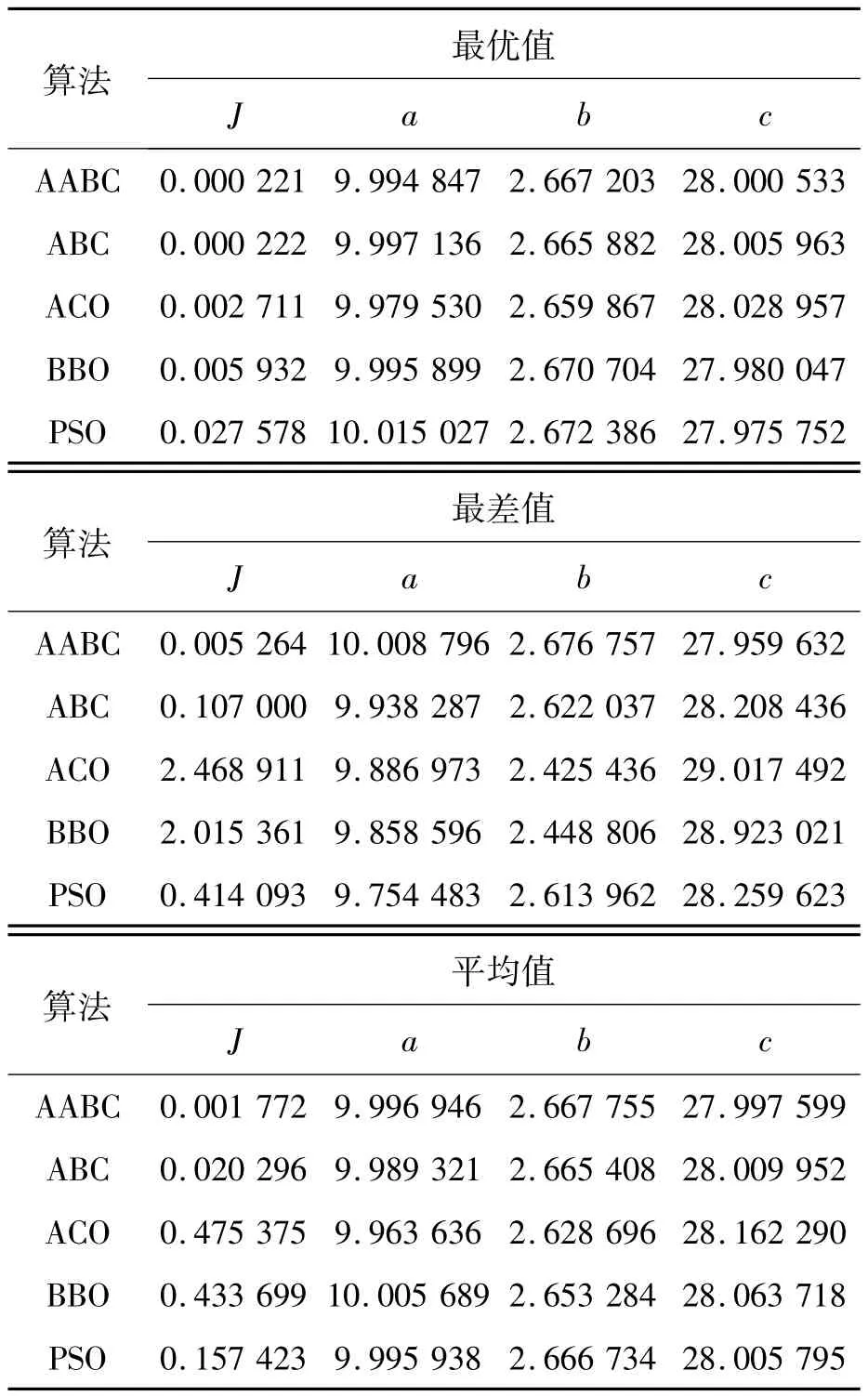
表1 无噪声情况下Lorenz系统参数估计结果Tab.1 Results of parameter estimation for Lorenz system without noise

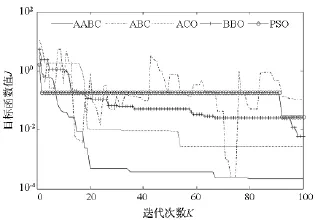
图2 目标函数J(θ)收敛曲线Fig.2 Convergency curve of object function J(θ)

为了检验AABC算法在实际应用中的性能，在式(9)的状态变量中加入较强的高斯白噪声，得到式(10)，从而测试标准差δ=0.4情况下各种算法的估计能力。

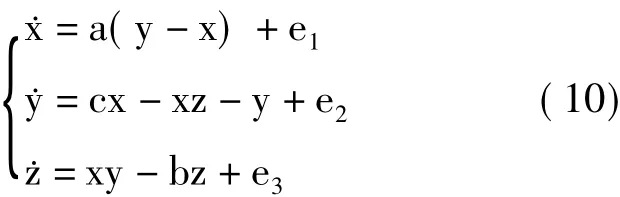
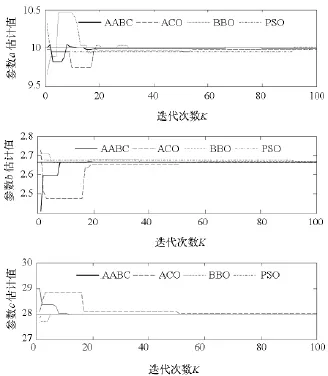
图3待估计参数a，b，c优化曲线Fig.3 Optimization curve of parameters a，b，c

图4 显示了所有算法目标函数J(θ)获得最优结果时的迭代收敛曲线。从图4中可以看到，在δ=0.4白噪声强度下AABC算法和BBO算法具有较好的收敛性，基本ABC算法、ACO算法和PSO算法表现出剧烈的波动。图4中曲线波动越小，说明算法的精确度越高。虽然在图4中，算法迭代前期的最优结果区别不大，但最终AABC算法的精确度显著优于其他算法，说明AABC算法在实际应用具有噪声的情况下仍然能够保持较好的性能。

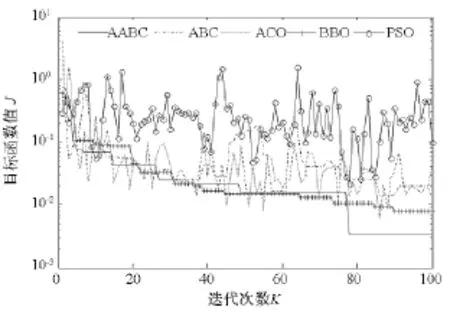
图4 δ=0.4时J(θ)收敛曲线Fig.4 Convergency curve of J(θ)whileδ=0.4

表2给出了高斯白噪声强度δ=0.4时，各算法参数估计的最优值、最差值和平均值。虽然在最优情况下AABC算法、ACO算法和BBO算法具有相近的精确度，但是在最坏情况和平均情况下AABC算法具有1～2个数量级的优势，表明了AABC算法具有较强的鲁棒性。

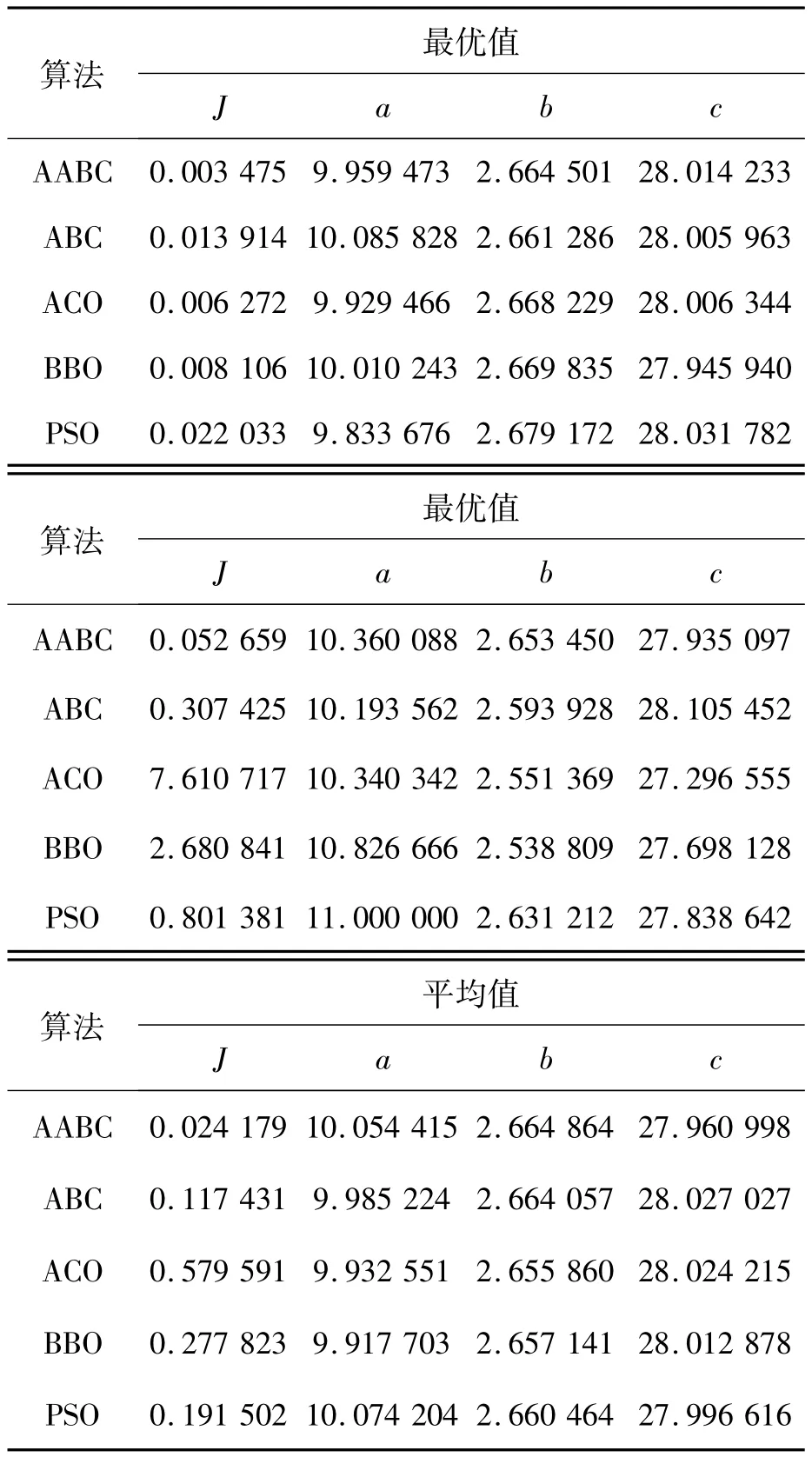
表2 噪声强度δ=0.4时Lorenz系统参数估计结果Tab.2 Results of parameter estimation for Lorenz system whileδ=0.4

4 结论

将混沌系统未知参数估计问题形式化为一个多维变量的数值优化问题，将人工蜂群优化算法引入到该问题的求解中并针对基本蜂群优化算法的不足提出改进的人工蜂群优化算法AABC。新算法根据种群优化程度选择更新步长，基于解的优异程度设置解的尝试次数，实现了算法迭代过程中的自适应优化。以Lorenz混沌系统为例进行的仿真实验表明，在无噪声和较大强度高斯白噪声情况下，AABC算法的参数估计结果均优于基本ABC，ACO，BBO和PSO算法，同时AABC算法在迭代过程中也表现出较强的鲁棒性。

参考文献(References)

［1］Ott E，Grebogi C，Yorke J A.Controlling chaos［J］.Physical Review Letters，1990，64(11):1196-1199.

［2］曹小群，宋君强，张卫民，等.基于MCMC方法的Lorenz混沌系统的参数估计［J］.国防科技大学学报，2010，32(2): 68-72.CAO Xiaoqun，SONG Junqiang，ZHANG Weimin，et al.Estimating parameters of Lorenz chaotic system with MCMC method［J］.Journal of National University of Defense Technology，2010，32(2):68-72.(in Chinese)

［3］戴栋，马西奎，李富才，等.一种基于遗传算法的混沌系统参数估计方法［J］.物理学报，2002，51(11):2459-2462.DAIDong，MA Xikui，LI Fucai，et al［J］.Acta Physica Sinica，2002，51(11):2459-2462.(in Chinese)

［4］王钧炎，黄德先.基于混合差分进化算法的混沌系统参数估计［J］.物理学报，2008，57(5):2755-2760.WANG Junyan，HUANG Dexian.Parameter estimation for chaotic systems based on hybrid differential evolution algorithm［J］.Acta Physica Sinica，2008，57(5):2755-2760.(in Chinese)

［5］Li N Q，Pan W，Yan L S，et al.Parameter estimation for chaotic systems with and without noise using differential evolution-based method［J］.Chinese Physics B，2011，20(6):72-77.

［6］林剑，许力.基于混合生物地理优化的混沌系统参数估计［J］.物理学报，2013，62(3):66-72.LIN Jian，XU Li.Parameter estimation for chaotic systems based on hybrid biogeography-based optimization［J］.Acta Physica Sinica，2013，62(3):66-72.(in Chinese)

［7］李丽香，彭海朋，杨义先，等.基于混沌蚂蚁群算法的Lorenz混沌系统的参数估计［J］.物理学报，2007，56(1):51-55.LILixiang，PENG Haipeng，YANG Yixian，et al.Parameter estimation for Lorenz chaotic systems based on chaotic ant swarm algorithm［J］.Acta Physica Sinica，2007，56(1): 51-55.(in Chinese)

［8］Peng H，Li L，Yang Y，et al.Parameter estimation of dynamical systems via a chaotic ant swarm［J］.Physical Review E，2010，81(1):016207.

［9］He Q，Wang L，Liu B.Parameter estimation for chaotic systems by particle swarm optimization［J］.Chaos，Solitons＆Fractals，2007，34(2):654-661.

［10］Sun J，Zhao J，Wu X J，et al.Parameter estimation for chaotic systemswith a drift particle swarm optimization method［J］.Physics Letters A，2010，374(28):2816-2822.

［11］张宏立，宋莉莉.基于量子粒子群算法的混沌系统参数辨识［J］.物理学报，2013，62(19):106-111.ZHANG Hongli，SONG Lili.Parameter identification in chaotic systems by means of quantum particle swarm optimization［J］.Acta Physica Sinica，2013，62(19):106-111.(in Chinese)

［12］Ouyang A，Tang Z，Li L，et al.Estimating parameters of Muskingum model using an adaptive hybrid PSO algorithm［J］.International Journal of Pattern Recognition and Artificial Intelligence，2014，28(1):1-29.

［13］Karaboga D，Basturk B.On the performance of artificial bee colony(ABC)algorithm［J］.Applied Soft Computing，2008，8(1):687-697.

［14］Karaboga D，Akay B.A comparative study of artificial bee colony algorithm［J］.Applied Mathematics and Computation，2009，214(1):108-132.

［15］Karaboga D，Basturk B.A powerful and efficientalgorithm for numerical function optimization:artificial bee colony(ABC) algorithm［J］.Journal of Global Optimization，2007，39(3): 459-471.

［16］高洪元，李晨琬.膜量子蜂群优化的多目标频谱分配［J］.物理学报，2014，63(12):456-465.GAOHongyuan，LIChenwan.Membrane-inspired quantum bee colony algorithm for multiobjective spectrum allocation［J］.Acta Physica Sinica，2014，63(12):456-465.(in Chinese)

［17］张乐，刘忠，张建强，等.基于人工蜂群算法优化的改进高斯过程模型［J］.国防科技大学学报，2014，36(1): 154-160.ZHANG Le，LIU Zhong，ZHANG Jianqiang，et al.Optimized improved Gaussian process model based on artificial bee colony algorithm［J］.Journal of National University of Defense Technology，2014，36(1):154-160.(in Chinese)

［18］Simon D.Biogeography-based optimization［J］.IEEE Transactions on Evolutionary Computation，2008，12(6): 702-713.

Adaptive artificial bee colony optim ization for parameter estimation of chaotic systems

REN Kaijun，DENGKefeng，LIU Shaowei，SONG Junqiang
(Academy of Ocean Science and Engineering，National University of Defense Technology，Changsha 410073，China)

In order to accurately estimate the unknown parameters for chaotic systems，the artificial bee colony optimization algorithm was improved，and an adaptive artificial bee colony optimization algorithm was proposed.The proposed method formatted the problem of parameter estimation for chaotic systems to amultidimensional variable optimization problem，and used the artificial bee colony optimization algorithm to search the unknown parameters in a guided random manner.During the search process，themethod adaptively adjusted the step size and the solution trial limits based on the optimum degree of the population and the quality of the solutions.The numerical simulation on the classic Lorenz chaotic system demonstrates that the proposed method is robust and can obtain accurate estimation for chaotic systems without noise or with intensive noise.

chaotic system；parameter estimation；artificial bee colony；numerical optimization

O302

A

1001-2486(2015)05-135-06

10.11887/j.cn.201505021

http://journal.nudt.edu.cn

2015-07-07

国家自然科学基金资助项目(61572510)；国家公益行业专项计划资助项目(GYHY201306003)

任开军(1975—)，男，重庆人，副研究员，博士，E-mail:renkaijun@nudt.edu.cn