拉伸-剪切耦合层合板优化设计及其应用*

李谨，唐国金(国防科技大学航天科学与工程学院，湖南长沙410073)

拉伸-剪切耦合层合板优化设计及其应用*

李谨，唐国金
(国防科技大学航天科学与工程学院，湖南长沙410073)

针对标准铺层拉伸-剪切耦合层合板耦合效应弱的缺点，提出利用优化法的自由铺层拉伸-剪切耦合层合板的设计方法。推导了只具有拉伸-剪切耦合效应的层合板应满足的条件。优化得到了7～14层的自由铺层拉伸-剪切耦合对称层合板。对比分析了自由与标准铺层拉伸-剪切耦合层合板的屈曲强度与稳定性。采用自由铺层拉伸-剪切耦合层合板设计了拉伸-扭转耦合结构。研究表明:自由铺层的拉伸-剪切耦合层合板的屈曲强度以及稳定性要显著弱于标准铺层层合板，但具有更强的耦合效应；随着层数的增加，自由铺层的拉伸-剪切耦合层合板的最大耦合效应逐渐减小。

拉伸-剪切耦合效应；层合板；优化设计；屈曲强度；拉伸-扭转耦合

图1 拉伸-剪切耦合效应Fig.1 Extension-shear coupling

利用复合材料层合板(以下简称层合板)的耦合效应可以设计多种类型的耦合结构［1-4］。其中，具有拉伸-剪切耦合效应的层合板(如图1所示)被广泛用于各种拉伸-扭转、弯曲-扭转耦合结构的设计。Nixon［5］采用具有拉伸-剪切耦合效应的对称均衡层合板，设计了具有拉伸-扭转耦合效应的倾转旋翼机桨叶；然而这种对称均衡层合板不仅具有拉伸-剪切耦合效应，还具有显著的弯曲-扭转耦合效应，弯曲-扭转耦合效应不但会显著降低层合板的屈曲强度［6］，还会使结构的耦合行为变得复杂。Baker［7］采用对称非均衡的拉伸-剪切耦合层合板，设计了具有弯曲-扭转耦合效应的机翼结构；类似的，这种对称非均衡的拉伸-剪切耦合层合板也具有显著的弯曲-扭转耦合效应。针对上述不足，York［8］设计了一种采用标准铺层(铺层角为±45°，0°，90°)的拉伸-剪切耦合非对称层合板，这种类型的层合板只具有拉伸-剪切耦合效应而不具有其他耦合效应，从而避免了弯曲-扭转耦合效应对层合板屈曲强度和结构耦合行为的不良影响；然而此种类型层合板的拉伸-剪切耦合效应较弱，制约了其在耦合结构中的应用。

1 拉伸-剪切耦合层合板设计

基于经典层合板理论，层合板的刚度方程可写为

式中，Nx，Ny，Nxy与Mx，My，Mxy分别为层合板单位宽度的内力以及内力矩，εx，εy，γxy为层合板中面应变，κx，κy，κxy为层合板中面弯曲曲率和扭曲率。Aij，Bij，Dij分别为拉伸刚度系数、耦合刚度系数和弯曲刚度系数。层合板的刚度系数可用两组相互独立的参数表示:仅与单层板材料属性相关的材料常数(Ui)和仅与铺层规律相关的几何因子(ξi)［10］。如式(2)～(4)所示。

其中，几何因子与材料常数的表达式如式(5)～ Qij为单层板材料主方向上的刚度系数，θk为第k层单层板的铺层角，zk为第k层单层板到中面的距离(中面以上为负，中面以下为正)，H为层合板厚度。

根据定义，拉伸-剪切耦合层合板的刚度系数应满足:拉伸刚度矩阵A中的所有元素都不为零，耦合刚度矩阵B等于零，弯曲刚度矩阵D中的弯曲-扭转耦合项(D16，D26)等于零。即拉伸-剪切耦合层合板的刚度方程应满足

依据式(2)～(4)，可以得到拉伸-剪切耦合层合板的铺层规律应满足的充要条件为

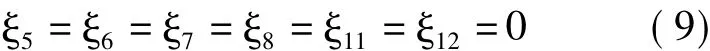
根据式(5)几何因子的定义，式(9)可以表示为

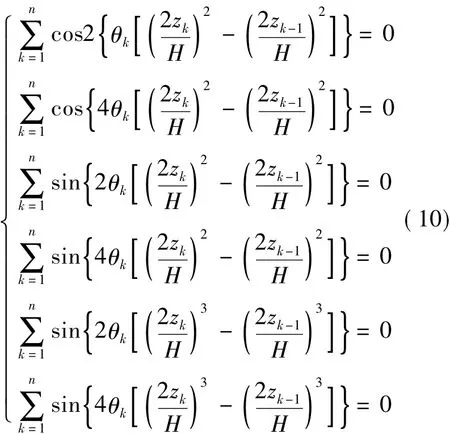
理论上，求解式(10)所列的由6个方程组成的方程组就可以得到拉伸-剪切耦合层合板的铺层规律。但这要求方程组中未知量(即每一层单层板的铺层角度)的个数必须不超过6个，否则方程难以求解。显然，在实际设计过程中难以通过直接求解方程的方法来得到满足设计要求的拉伸-剪切耦合层合板。

考虑到自由铺层层合板的铺层角度是区间(-90°，90°］上的连续变量，引入优化设计的方法来求解拉伸-剪切耦合层合板的铺层规律。以层合板每一层的铺层角度作为优化设计变量，以拉伸-剪切耦合效应最大作为优化目标，以式(9)所示的拉伸-剪切耦合层合板应满足的条件作为优化约束条件，将层合板的铺层设计问题转化为带约束的优化设计问题。层合板的拉伸-剪切耦合效应最大可等效为其拉伸-剪切耦合柔度系数最大。故此优化问题可表示为

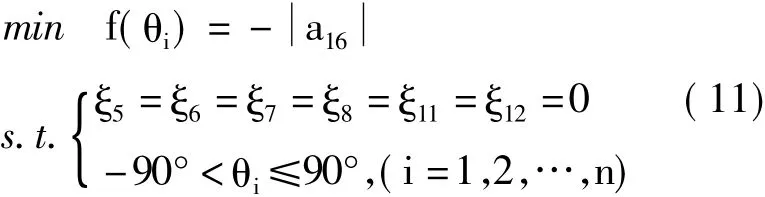
其中，a16为层合板的拉伸-剪切耦合柔度系数，可以由式(12)求得。需要说明的是，在此优化过程中仅以层合板的耦合效应为优化目标，但在实际结构设计时还应根据需要引入其他设计指标，例如屈曲强度、刚度等，以确保得到的铺层规律满足结构设计要求。

为了减少优化变量，将优化对象限定为对称层合板。采用序列二次规划法求解此优化问题。序列二次规划法是一种依赖于目标梯度的优化算法，而作为优化目标的拉伸-剪切耦合柔度系数并不是一个单峰函数。为了避免优化得到的仅是局部最优解，采用随机生成初值进行多次优化，再从多次优化的结果中选取最优解的方法来确保最终得到的优化结果是全局最优解。求解过程中选用的单层板材料参数见表1。

表1 材料参数Tab.1 Material properties

表2给出了优化得到的7～14层自由铺层拉伸-剪切耦合对称层合板的铺层规律。考虑到实际工艺的精度，将表2中所列铺层的铺层角圆整到小数点后1位，圆整的结果见表3。需要说明的是，由于对优化得到的精确结果进行了圆整处理，表3中的部分铺层规律并不能严格满足拉伸-剪切耦合层合板的条件。从表3中可以看出，随着层数的增加，自由铺层拉伸-剪切耦合层合板的最大拉伸-剪切耦合效应在逐渐减小。这是由于随着层合板的厚度增加，层合板的剪切刚度也在逐渐增大。

表2 自由铺层拉伸-剪切耦合层合板Tab.2 Free-form laminates with extension-shear coupling

表3 圆整后的自由铺层拉伸-剪切耦合层合板Tab.3 Rounding free-form laminates with extension-shear coupling

文献［8］得到了4种14层的标准铺层拉伸-剪切耦合非对称层合板，见表4。计算发现，表4中编号1，2和编号3，4的标准铺层层合板分别具有相同的刚度系数，分别将其命名为S1和S2。对比表3与表4可以发现，自由铺层层合板的拉伸-剪切耦合效应要显著强于标准铺层层合板。

表4 标准铺层拉伸-剪切耦合层合板Tab.4 Standard-form laminateswith extension-shear coupling

2 屈曲强度分析

为了对比自由与标准铺层拉伸-剪切耦合层合板的屈曲强度，选取表3中的自由铺层拉伸-剪切耦合层合板与表4中的标准铺层拉伸-剪切耦合层合板进行分析。

考虑均布单向平面压力下的简支矩形层合板，如图2所示，其四边简支，沿x方向受到均匀平面力的作用。

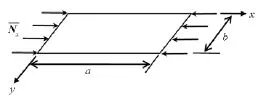
图2 均布单向平面压力下的简支矩形层合板Fig.2 Simply supported laminated rectangular plate under uniform uniaxial in-plane compression

拉伸-剪切耦合层合板的屈曲方程［9］可表示为

但是，式(16)中的弯曲刚度系数D22会随着铺层角度的变化而变化，这会影响不同层合板的屈曲强度的对比结果。因此引入和铺层角无关的等效弯曲刚度DIso［11］代替D22，则式(16)可以表示为

图3给出了标准铺层拉伸-剪切耦合层合板与7～14层自由铺层拉伸-剪切耦合层合板的屈曲载荷随板长宽比的变化曲线。由于7～14层自由铺层拉伸-剪切耦合层合板的屈曲载荷曲线区别很小，所以图3中只标示出其上、下边界。从图3中可以看出:自由铺层拉伸-剪切耦合层合板的屈曲强度要显著弱于标准铺层拉伸-剪切耦合层合板的；7～14层自由铺层拉伸-剪切耦合对称层合板中，11层拉伸-剪切耦合层合板的屈曲载荷最大，9层拉伸-剪切耦合层合板的屈曲载荷最小。

图3 拉伸-剪切耦合层合板屈曲载荷Fig.3 Buckling load for laminateswith extension-shear coupling

3 稳定性分析

由于拉伸-剪切耦合层合板的耦合刚度矩阵B等于零，所以不论采用对称铺层还是非对称铺层，理论上其在固化时均不会因为温/湿度变化而产生翘曲变形。然而实际铺层角与理论设计值之间不可避免地会存在偏差，从而会导致拉伸-剪切耦合层合板发生固化翘曲变形。为了确保设计出的拉伸-剪切耦合层合板具有实用性，实际铺层角与理论设计值间的细微偏差不应导致层合板发生显著的固化翘曲变形。为此下面采用Monte Carlo法分析铺层角度存在偏差时拉伸-剪切耦合层合板的固化翘曲变形。利用Monte Carlo法分析层合板稳定性的途径可归纳为三个基本步骤:

1)随机参数抽样，根据随机参数的已知概率分布进行随机抽样；

2)层合板响应求解，针对每个抽取样本，基于经典层合板理论求解层合板的响应(如温度改变时层合板的翘曲变形等)；

3)响应量的统计分布。

分别选取表3中14层自由铺层拉伸-剪切耦合层合板和表4中14层标准铺层拉伸-剪切耦合层合板为例进行对比分析。

为了直观描述层合板固化翘曲变形的程度，采用文献［10］提出的方法，用温度变化引起的层合板挠度变化表征层合板的固化翘曲变形的程度。设某矩形层合板的长度与宽度分别为a，b，建立如图4所示的坐标系。层合板在(0，0)、(a，0)、(0，b)三个角点处简支，在角点(a，b)处自由。当温度变化时，层合板上任一点的挠度可表示为

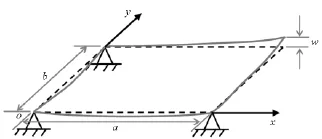
图4 矩形层合板的热挠度Fig.4 Deflection of a rectangular laminate

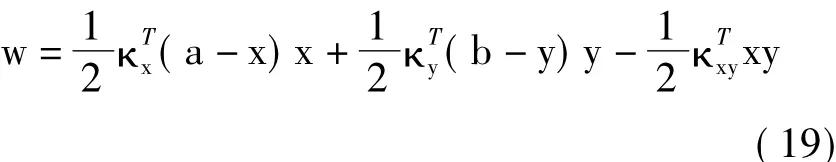
则温度变化引起的层合板自由角点处的挠度可表示为

用层合板的厚度H对挠度进行无量纲化处理，可以得到

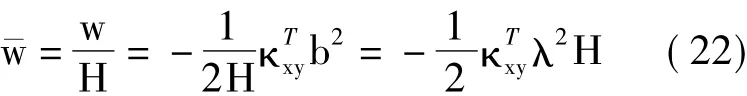
采用式(22)计算温度改变时层合板自由角点处的挠度。计算过程中选取典型高温固化过程的温度改变量ΔΤ=-180℃［11］。假定实际铺层角与理论设计值之间的偏差随机分布在区间［-1°，1°］上，每次抽取10 000组偏差样本进行分析。

图5与图6分别给出了温差为-180℃时，14层自由和标准铺层拉伸-剪切耦合层合板的挠度等距频率直方图。由图5、图6可以得出如下结论:铺层角存在偏差时，14层自由铺层拉伸-剪切耦合层合板的热挠度分布在区间［-1.6H，1.6H］上；铺层角存在偏差时，14层标准铺层拉伸-剪切耦合层合板的热挠度分布在区间［-0.4H，0.4H］上；相比于自由铺层，存在铺层偏差的标准铺层拉伸-剪切耦合层合板产生的热挠度更小，即标准铺层拉伸-剪切耦合层合板具有更好的湿热翘曲变形稳定性。

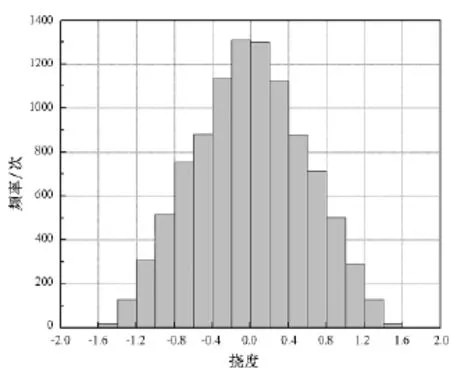
图5 14层自由铺层拉伸-剪切耦合层合板存在铺层角度偏差时的热挠度等距频率直方图Fig.5 Histograms of thermal deflection because of layup errors for 14-ply free-form extension-shear coupled laminate

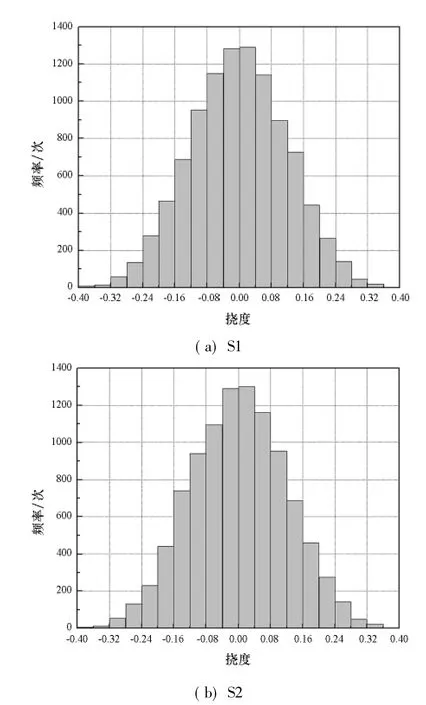
图6 14层标准铺层拉伸-剪切耦合层合板存在铺层角度偏差时的热挠度等距频率直方图Fig.6 Histograms of thermal deflection because of layup errors for14-ply standard-form extension-shear coupled laminate

4 拉伸-扭转耦合结构设计

拉伸-剪切耦合层合板可以用于多种耦合结构的设计，例如拉伸-扭转耦合倾转旋翼机桨叶［5］、拉伸-扭转耦合自适应风力发电机叶片［3］等。下面采用本文得到的自由铺层拉伸-剪切耦合层合板设计拉伸-扭转耦合结构，并运用有限元法对悬臂梁的耦合效应进行验证。

不论是风机叶片还是倾转旋翼机桨叶，都可以将其简化为盒形悬臂梁模型。将得到的自由铺层拉伸-剪切耦合层合板布置为悬臂梁的上面板，悬臂梁下面板的铺层角与上面板的互为相反数，这样就可以确保上、下面板在方向相同的轴向力的作用下产生方向相反的剪切变形。左、右腹板为各向同性材料。当悬臂梁受到轴向力作用时，上、下面板发生方向相反的剪切变形，如图7所示，进而引起整个梁的扭转变形，如图8所示。

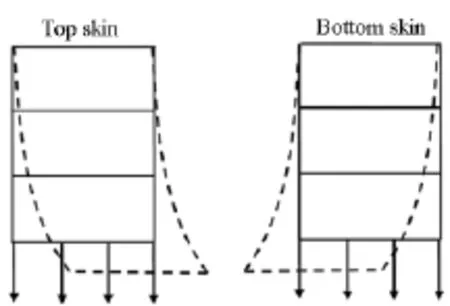
图7 上下面板变形Fig.7 Deformation of the top and bottom skins

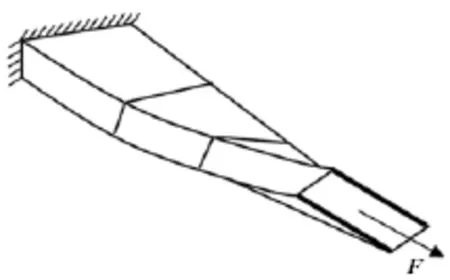
图8 拉伸-扭转耦合变形Fig.8 Extension-twist coupled deformation

采用有限元法对上述盒型悬臂梁的拉伸-扭转耦合效应进行数值仿真。采用四节点壳单元建立盒型悬臂梁有限元模型，梁长3m，矩形截面尺寸为0.3m×0.13m，如图9所示。将表3中7层自由铺层拉伸-剪切耦合层合板布置为悬臂梁的上面板，悬臂梁下面板的铺层角与上面板的互为相反数。悬臂梁一端固支，自由端施加5kN的轴向拉力。仿真过程选用表1所示的单层板材料参数。

图10给出了悬臂梁在自由端轴向拉力作用下的位移云图。从图10中可以看出，在轴向拉力作用下，盒型梁发生了显著的扭转变形，梁的自由端转角约为0.21°，从而验证了结构的拉伸-扭转耦合效应。

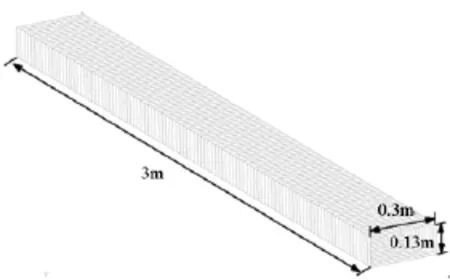
图9 盒型悬臂梁有限元模型Fig.9 Finite elementmodel of a cantilever box-beam

图10 盒型悬臂梁拉力作用下的变形示意图Fig.10 Deformation of a cantilever box-beam relating an applied axial force

5 结论

1)存在自由铺层的拉伸-剪切耦合对称层合板，其最大拉伸-剪切耦合效应要显著强于标准铺层拉伸-剪切耦合层合板。

2)自由铺层拉伸-剪切耦合层合板的最大拉伸-剪切耦合效应随着层数的增加逐渐减小。

3)通过最优化耦合效应得到的自由铺层拉伸-剪切耦合对称层合板的屈曲强度与稳定性要显著弱于标准铺层拉伸-剪切耦合层合板。因此实际应用中应根据需要引入其他设计指标，例如屈曲强度、刚度等，以确保得到的铺层满足结构设计要求。

References)

［1］万志强，杨超.大展弦比复合材料机翼气动弹性优化［J］.复合材料学报，2005，22(3):145-149. WAN Zhiqiang，YANG Chao.Aeroelastic optimization of a high-aspect-ratio composite wing［J］.Acta Materiae Composite Sinica，2005，22(3):145-149.(in Chinese)

［2］万志强，邵珂，杨超，等.非均衡铺层壁板复合材料机翼气动弹性分析［J］.复合材料学报，2008，25(1): 196-199.WAN Zhiqiang，SHAO Ke，YANG Chao，et al.Aeroelastic analysis of composite wings with unbalance laminates［J］.Acta Materiae Composite Sinica，2008，25(1):196-199.(in Chinese)

［3］刘旺玉，龚佳兴，刘希凤，等.基于弯扭耦合的自适应风力机叶片设计［J］.太阳能学报，2011，32(7): 1014-1019.LIU Wangyu，GONG Jiaxing，LIU Xifeng，et al.The adaptive blade design ofwind turbine based on beam flap-twist coupling theory［J］.Acta Energiae Solaris Sinica，2011，32(7):1014-1019.(in Chinese)

［4］周磊，万志强，杨超.复合材料壁板铺层参数对大展弦比机翼气动弹性优化的影响［J］.复合材料学报，2013，30(5):195-200.ZHOU Lei，WAN Zhiqiang，YANG Chao.Effect of laminate parameters of composite skin on aeroelastic optimization of high-aspect-ratio wing［J］.Acta Materiae Composite Sinica，2013，30(5):195-200.(in Chinese)

［5］Nixon M W.Extension-twist coupling of composite circular tubes with application to tit rotor blade design［C］// Proceedings of the AIAA/ASME/ASCE/AHS 28th Structures，Structural Dynamic and Materials Conference，1987:295-303.

［6］沈观林，胡更开.复合材料力学［M］.北京:清华大学出版社，2006:163-164.SHEN Guanlin，HU Gengkai.Mechanics of composite materials［M］.Beijing:Tsinghua University Press，2006: 163-164.(in Chinese)

［7］Baker D J.Response of damaged and undamaged tailored extension-shear-coupled composite panels［J］.Journal of Aircraft，2006，43(2):517-527.

［8］York C B.On extension-shearing coupled laminates［J］.Composite Structures，2015，120:472-482.

［9］Jones R M.Mechanics of compositematerials［M］.2nd ed.USA:Taylor and Francis Inc，1999:301-315.

［10］Tsai SW，Hahn H T.Introduction to compositematerials［M］.USA:Technomic Publishing，1980:349-354.

［11］York C B.Unified approach to the characterization of coupled composite laminates:hygro-thermally curvature-stable configurations［J］.International Journal of Structural Integrity，2011，2(4):406-436.

Optim ization design of extension-shear coup led lam inates and application in extension-tw ist coup led structure

LIJin，TANG Guojin
(College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Focusing on the deficiencies of standard-form laminate with extension-shear coupling，such as weak extension-shear coupling，the design method for free-form laminatewith extension-shear coupling using themethod of optimization design was proposed.Necessary and sufficient material-independent conditions were derived for extension-shear coupled laminates.The stacking sequences of 7-ply to 14-ply free-form laminates with extension-shear couplingwere derived.Comparisonsweremade on buckling strength and robustness of extension-shear coupled laminates.The free-form laminate with extension-shear coupling was used to design structure with extension-twist coupling.Compared to the standard-form laminate，the free-form laminate with extension-shear coupling is worse in buckling strength and robustness，while it’s stronger in coupling.The results also indicate that with an increase in the number of plies，the maximum extension-shear coupling flexibility coefficient of the free-form laminate decreases.

extension-shear coupling；laminate；optimization design；buckling strength；extension-twist coupling

TB330.1

A

1001-2486(2015)05-121-07

10.11887/j.cn.201505019

http://journal.nudt.edu.cn

2014-11-25

国家自然科学基金资助项目(11472003)

李谨(1986—)，男，江苏连云港人，博士研究生，E-mail:lijin@nudt.edu.cn；唐国金(通信作者)，男，教授，博士，博士生导师，E-mail:tanggj@nudt.edu.cn