地籍数据库点线拓扑一致性并行检查方法*

杨宜舟，吴立新，2，郭甲腾，刘善军(.东北大学测绘遥感与数字矿山研究所，辽宁沈阳089；2.中国矿业大学物联网(感知矿山)研究中心，江苏徐州22008)

地籍数据库点线拓扑一致性并行检查方法*

杨宜舟1，吴立新1，2，郭甲腾1，刘善军1
(1.东北大学测绘遥感与数字矿山研究所，辽宁沈阳110819；2.中国矿业大学物联网(感知矿山)研究中心，江苏徐州221008)

针对拓扑检查算法复杂、计算量大，串行计算已远不能满足海量地籍数据高效拓扑检查需求的问题，在分析了点线拓扑关系的并行特点基础上，将界址点的数据划分方法与界址线的Q＆R空间索引方法相结合，实现了界址点与界址线的并行拓扑计算。用某地区实际的界址点集与界址线集对点线拓扑并行检查进行实验。测试结果表明:并行检查算法的并行效率随着进程数的增加而有所衰减，但稳定在30%以上，加速比达到5以上，且相比于ArcGIS效率提升了30倍以上。并行检查方法以工具的方式集成应用于高性能地理计算平台中，应用效果良好。

地籍数据库；拓扑关系；数据质量；并行计算；高性能地理计算平台

地籍数据库作为空间数据库的一种，其涉及的土地权属要素为:界址点、界址线及宗地。基于规则的拓扑一致性检查是土地权属要素质量检查的研究重点，而界址点与界址线之间的重合检查属于地籍数据拓扑一致性检查中重要部分［1］。地籍数据库的质量控制问题一直是国际地籍学术界和产业界的前沿研究领域，其研究内容包括空间数据位置精度、语义属性精度与逻辑一致性，而其中的研究热点是地籍数据的逻辑一致性，核心问题为拓扑一致性的维护问题［2］。地籍拓扑一致性维护的重要组成部分是空间拓扑检查，是拓扑关系在地籍数据质量控制中的应用。由于不同平台空间拓扑的要求、空间组织与表达的差异性，特别是空间数据的采集精度、采用的技术方法不一致导致了地籍数据之间难以统一［3］。随着国土资源“一张图”建设全面展开，地籍数据的数据量也日益增长［4］，而且地籍数据本身的空间复杂性使传统串行环境下的空间拓扑检查方法已远不能满足实际应用中地籍数据拓扑一致性高效检查的需求。虽然近年计算机计算能力迅速提高，尤其是多核计算机和并行计算机开始普及，但传统拓扑检查的串行算法却难以充分利用这些先进的计算资源［5］。因此，如何充分利用这些新的计算资源来解决更复杂的实际应用，已成为目前十分关注的问题。在信息领域，并行计算为协同利用更多的计算资源提供了新的手段，实现了利用多个计算节点的计算资源来提高计算能力［6］，为高效处理大规模空间数据的拓扑关系检查提供了理论和技术支撑。传统的商业软件需在建立全局拓扑关系基础上，通过全局拓扑关系来查询与目标对象相邻(相交)的空间对象进行拓扑检查(快速过滤不与目标对象相交的空间对象集)；但在大数据的环境下建立全局拓扑关系耗时较长难以满足高效拓扑检查的需求［7-9］。现已有部分地理计算平台(Geographic Information System，GIS)算法通过数据划分基本实现并行计算［10］，但串行拓扑检查需要全局拓扑关系，难以通过划分全局拓扑关系来实现拓扑检查的并行化［11］。特别是对于点线拓扑计算的多图层数据，仅利用现有数据划分方法［12-15］不能有效提升拓扑并行计算的效率，其难点在于:在数据划分的基础上需实现目标对象与其相邻空间数据的高效查询(即高效过滤与目标对象不相交的空间对象集，而数据划分破坏了全局拓扑关系)。杨宜舟等在分析了点线拓扑关系计算特点的基础上，通过对点(界址点)的单图划分，对线(界址线)建立空间索引，实现点线拓扑检查的并行化。同时，集成在新一代高性能GIS——高性能地理计算平台(High Performance GIS，HiGIS)中。

1 拓扑关系基本原理

目前，空间拓扑关系的计算模型有基于点集理论的描述模型(4交模型［16］与9交模型［17］)、基于区域连接演算(Region Connection Calculus，RCC)理论的描述模型［18］、基于Voronoi图的9交模型［19］等。基于点集理论的9交模型是当前最为常用的拓扑关系分析和计算模型，具有广泛的适用范围和较高的计算效率，相比其他两种描述模型更适合于高性能拓扑关系的计算。在目前商业软件中，主要是使用9交模型计算目标间的拓扑关系，最具代表性的Oracle和ArcGIS均采用基于点集理论维度扩展的9交模型，分别实现空间关系的查询和GIS拓扑分析的功能。采用开放地理信息系统协会(Open GISConsortium，OGC)基于点集理论维度扩展的9交模型(Dimensionally Extended Nine-Intersection Model，DE-9IM)作为描述简单要素间拓扑关系的模型。根据这8种拓扑关系之间的联系，可确定一个最小覆盖关系集。该最小拓扑关系集中包含5种关系类型:相离(disjoints)、相接(touches)、叠加(overlaps)、包含(within/contains)和穿越(crosses)。这5种关系能对所有的空间关系构成一个完整的覆盖，它们是基本的、互斥的。因为在点线拓扑关系中仅有相离、包含两种关系，所以仅针对这两种关系进行研究。

2 界址点与界址线拓扑与并行计算

2.1 界址点与界址线拓扑并行分析

界址点与界址线拓扑一致性检查就是计算界址点是否在界址线上。界址点与界址线拓扑关系仅包含相离和包含两种类型，其中两者的相离关系为界址点不在界址线上，而包含关系是界址点在界址线上。地籍点线(界址点与界址线)拓扑一致性检查过程如图1所示，在界址点与界址线拓扑关系计算过程中先要判断点、线的外包围矩形(Minimum Bounding Rectangle，MBR)是否相交，若MBR为相交关系(intersects)，则在MBR相交关系的基础上进行线包含点的拓扑关系计算，若MBR不相交，则点、线之间为相离关系。因此，界址点与界址线拓扑关系之间的计算过程［20］为:

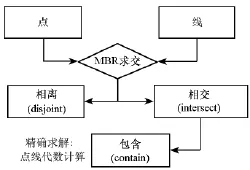
图1 点线拓扑关系计算过程Fig.1 Process of topology calculation of point-line

(1)界址点p与界址线集S进行相交检查，获取与界址点MBR相交的界址线集L={l1，l2，…，ln}。界址点与界址线之间先通过MBR之间相交计算，过滤掉大部分与目标界址点MBR相离的界址线。在数据过滤的过程中，若采用MBR直接过滤方法(遍历过滤)，在大数据环境下过滤过程的耗时将急剧增加(设界址点数为n，界址线数为m，各界址点都需通过遍历m次过滤相离的界址线，那么n个界址点则需要遍历n×m次，所以数据规模越大过滤所消耗的时间越长)，严重制约着界址点与界址线拓扑计算的效率，所以在界址点与界址线拓扑关系并行计算中需要提供一种通过MBR快速过滤大部分相离目标的方法。

(2)根据九交模型计算p与L中各界址线的拓扑关系结果为t(li)，若t(li)为拓扑包含关系，则界址点在界址线上，否则界址点不在界址线上。将界址点与界址线上每条线段进行计算，判断界址点是否在界址线上。点线判断算法如图2所示:点Q与线段两个端点P1和P2构成的向量间叉积为零，且点Q在线段所构成MBR内，则点Q在线段上，否则点在线段外。另外，对于点与线段两个端点重合的情况，则只需要判断点Q分别与P1和P2是否相等即可。由于与各界址点进行拓扑计算的界址线所包含的线段数目不同，则各界址点的计算量有所不同，即各界址点的计算量与界址线所包含的线段数目相关。界址线是由多个顶点组成，所以界址点与界址线拓扑的计算量与界址线所包含的顶点数目正相关。

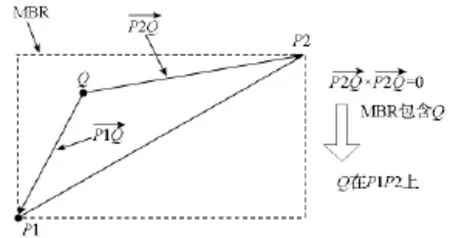
图2 点线判断过程Fig.2 Judgement process of point-line

据此，点线拓扑关系计算特点为:(1)点线拓扑需要高效过滤与界址点相离的界址线的方法；(2)点线拓扑关系计算中各界址点之间采用相同的计算流程完成计算(各单元之间的计算独立、互不影响)；(3)界址点与界址线拓扑关系的计算强度与界址线所包含的顶点数相关，即界址线的顶点数可体现界址点与界址线拓扑计算复杂度(计算量)。

根据点线拓扑关系计算特点1可知:现有空间数据过滤方法中最常用的是空间索引，所以需对参与计算的界址线建立空间索引，以提高界址线的过滤效率。根据点线拓扑关系计算特点2可知:将各界址点的计算作为子问题，各子问题之间的计算相互独立，即各进程间不需要进行通信和等待，对界址点直接进行划分即可实现点线拓扑计算的并行化。因此，根据界址点与界址线拓扑计算特点1与特点2，通过对点数据的空间划分、对线数据建立空间索引即可实现点线拓扑计算的并行化。根据界址点与界址线拓扑关系计算的特点3可知:界址点与界址线拓扑计算量的大小与界址线本身复杂度相关，即界址线包含的顶点数可反映点线拓扑计算的复杂程度，通过简单的界址点数据划分，并不能实现各进程界址点子集所对应的相交线集的顶点数均衡(任务均衡)的目的。因此，研究一种适合于界址点与界址线拓扑计算并行化的方法重点在于界址点集划分方法与界址线集的空间索引方法。

现有并行编程模型可分为3类［6］:消息传递模型、共享存储模型和数据并行模型。消息传递模型是目前使用最为广泛的并行模型，其有两大优势:(1)消息传递程序具有高度的可移植性，理论上可在任何并行机上执行，即不需要特殊的硬件支持；(2)允许用户显式地控制并行程序中每个进程内存的使用，为编程人员实现高性能计算提供便利。其并行程序开发模式通常有两种:单程序多数据［6］(Single Program Multiple Data，SPMD)模式和多程序多数据［6］(Multiple Program Multiple Data，MPMD)模式。因此，采用SPMD模式设计并行算法，根据界址点与界址线拓扑计算特点，通过界址点集的数据划分与界址线集的空间索引即可实现界址点与界址线拓扑计算的并行化。

2.2 界址点与界址线拓扑并行化方法

根据以上并行化特点分析，界址点与界址线拓扑检查的数据分为界址点、界址线两部分，在实现点线拓扑关系并行计算时两部分数据需分别处理，即对界址点集进行划分，对界址线集建立空间索引。界址点与界址线的拓扑检查的并行化方法如图3所示，首先，对界址点数据进行划分，将空间相邻的界址点划分至不同的计算节点；其次，对界址线建立Q＆R索引，实现各计算节点中界址点对MBR相交的界址线的快速查询；最后，各计算节点采用DE-9IM模型实现界址点与界址线的拓扑计算。

设界址点集为P={p1，p2，…，pn}，界址线集为L={l1，l2，…，lm}，界址点与各界址线之间计算量可表达为f(lj)(根据2.1节可知界址点与界址线的拓扑计算量大小与界址线所包含的顶点数正相关)，界址点影响域为z(pi)(即与界址点MBR相交的所有界址线)，界址点影响域内的计算量为f(pi，z(pi))，那么界址点集与界址线集的计算总量可表示为Σf(pi，z(pi))。界址线lj与其影响域z(li)中的g个界址点Si{pa，pb，…，px}进行计算(g个界址点具有空间邻近性)，其计算量可分解为g个f(lj)(Si中各点计算量相等，且Si中各点空间位置邻近)，所以在界址点与界址线拓扑计算中空间临近的界址点的影响域z(pi)基本一致，即空间邻近的界址点(pi，pi+1为相邻的界址点)的计算量基本相等(f(pi，z(pi))≈f(pi+1，z(pi+1)))。因此，在划分界址点集时需将空间临近的界址点划分至不同的进程进行计算，且海量的界址点与界址线进行拓扑计算时不能将全部数据读入内存(占用过多的计算资源)，应以分块方式计算。具体的步骤如下:

(1)通过深度为n的Q树对空间进行初次划分，每次计算以各Q树的叶子节点为一个单元；

(2)由于Hilbert值排序最能反映空间临近性，所以各进程分别对各Q树叶子节点中所包含的界址点进行Hilbert空间编码；

(3)利用并行空间排序算法对Hilbert空间编码进行排序；

(4)对各叶子节点中排序在后的界址点轮转地分配至各个进程；

(5)重复2～4步直至Q树所有叶子节点中的界址点分配完毕。

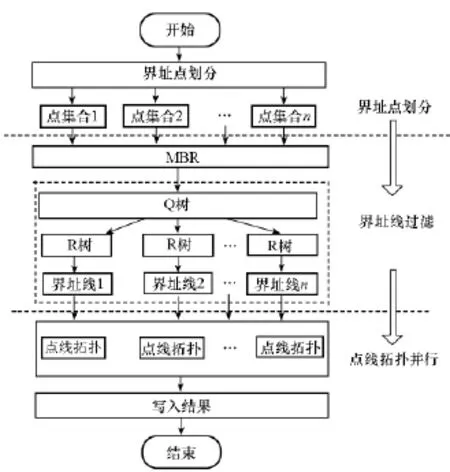
图3 界址点与界址线并行拓扑检查Fig.3 Parallel topology check of boundary points and boundary lines

界址点集采用Q划分与Hilbert划分结合的数据划分方法，将数据集分配至各计算节点(通过Q树划分使界址点数据分块，而Hilbert划分将空间相邻的界址点划分至不同的计算节点)。而界址线集则采用全冗余的策略，为避免在计算过程中占用过多的计算资源，也需要对界址线数据进行分块，并且需对界址线数据建立空间索引以满足拓扑计算过程中高效过滤的需求。因此，采用Q＆R混合索引实现界址线的分块索引(如图4所示)，具体步骤如下:

(1)计算空间对象集S中所有空间对象的最小包围盒rn，最小包围盒中心点cn；

(2)根据硬件的计算能力及空间对象集S的数目N，计算Q树叶子节点的平均容量ca和Q树的深度n；

(3)创建深度为n的Q树，并按照编码规则eC(可为任意有规律的编码规则，如Hilbert编码、Z曲线编码等)对所有的叶子节点进行编码，各叶子节点的编码为Cm(利用编码规则可扩展到全球尺度空间索引［21-22］)；

(4)根据编码规则eC对空间对象的中心点cn进行编码，并将该空间对象分配至与其编码相同的叶子节点(可快速定位Q树叶子节点，避免Q树根节点成为访问热点［23］)；

(5)重复步骤4直至所有的空间对象分配至Q树的叶子节点；

(6)各Q树叶子节点下的数据建立R树索引。

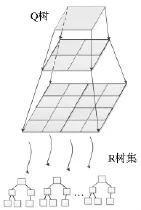
图4 Q＆R空间索引Fig.4 Q tree and R treemixed spatial index

上述过程中界址点的Q树划分与Q＆R混合空间索引采用的Q树是同一Q树，可使界址点的分块与界址线的分块相互对应。Q＆R混合空间索引中的Q树不仅有数据划分功能且具有空间索引的功能，实现了对R树集的索引，而Q＆R混合空间索引中R树集是实现界址线的检索(Q＆R混合空间索引属于双层空间索引)。Q＆R混合空间索引的平均时间复杂度O(log(n)+log(N/4n))(N为界址线数目，n为Q树深度)，优于时间复杂度为O(log(N))的R树空间索引。

设各进程已分配的界址点集为Pi={q1，q2，…，qn×n}，qj为Q树各叶子节点所包含的界址点子集，其中:0＜i≤p，0＜j≤n×n，p为进程总数，n为Q树深度。界址线集的Q＆R混合空间索引中Q树叶子节点对应的R树集为M={r1，r2，…，rn×n}，rj为界址线子集空间索引，其中:0＜j≤n× n，n为Q树深度。首先各进程中参与计算的界址点集qi通过MBR(或者利用qi对应Q树叶子节点的编码)检索其在界址线集Q＆R空间索引中的影响区域z(例如q1珋z(r1)，z(r1)为q1在界址线集中的影响域，通过z(r1)所在的R树查询MBR与q1中各界址点相交的界址线集)，然后将qj中各界址点与z(rj)中检索的界址线集进行拓扑计算(如图3所示)，直到所有的界址点计算完毕。

3 实验

3.1 测试环境与测试数据

为测试该方法的计算效率，搭建了一个小型集群的测试环境。该环境由4个高性能计算节点及1个存储节点(2T)构成，集群中各节点的操作系统是Redhat5.04(64位)，消息传递采用MPICH2的并行库。本案例为对某地区界址点与界址线的数据质量进行检查，本实验取某地区的174 327条界址线和1 668 276个界址点。

3.2 测试结果

本文方法并行拓扑计算结果与在相同环境下采用ArcGIS拓扑计算的结果一致，图5为两种方法的计算结果，其结果完全一致，图形完全重合，图5中五角星为点线拓扑不一致的结果。ArcGIS耗时约为15min，而本文方法在16进程下仅需26.87s即可完成计算，效率相比于串行的ArcGIS提升了30倍以上，而且本文方法也已集成应用在HiGIS平台中。由界址点与界址线拓扑关系并行计算加速比、并行效率(如图6所示)与进程数的统计关系(见表1)可见:本文方法的并行效率与进程数相关，即并行算法效率随着进程数增加而衰减，在16进程下的并行效率仍稳定在30%以上；加速比随进程数增加而增长，在16进程时达5.23。

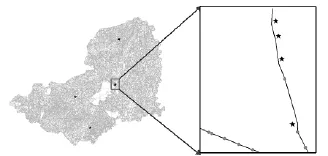
图5 界址点与界址线拓扑计算结果Fig.5 Results of topology calculation of boundary points and boundary lines

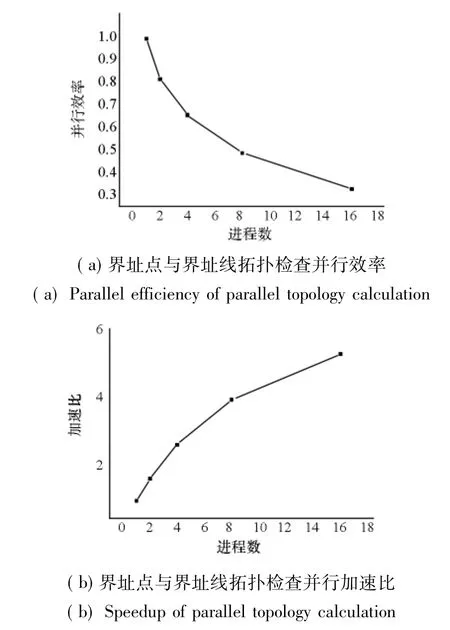
图6 并行效率与并行加速比Fig.6 Parallel efficiency and speedup of parallel topology calculation

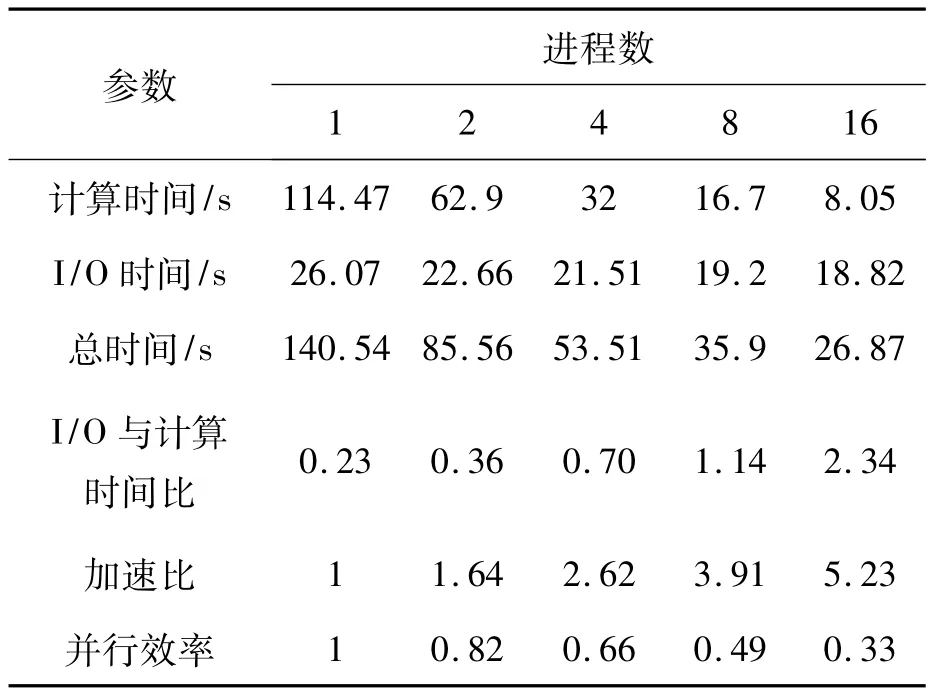
表1 点线拓扑计算测试结果Tab.1 Result of point-line topology calculation

由于测试数据受通信网络和地籍数据规模的影响，并行效率会随着进程数目的增加而逐渐衰减，加速比会随着进程数目的增加而趋于稳定。随着进程数目的增加，I/O(本文的I/O包含了数据划分时间与创建空间索引时间)的性能会成为影响并行算法解算的性能瓶颈。如图7所示，随着进程数的增加，各进程的计算任务量会逐渐减少，而I/O耗时比率会逐渐增加，若在更大规模的界址点与界址线数据下，本文的方法的效率将会有进一步的提升。

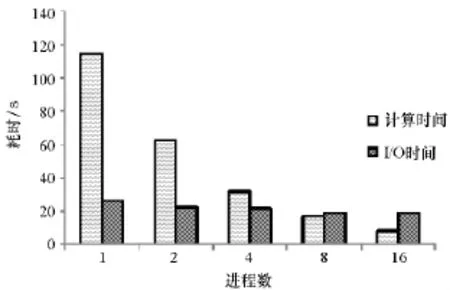
图7 计算时间与I/O时间对比Fig.7 Rratio of computing time and I/O time

4 结论

针对地籍数据质量检查中界址点与界址线拓扑一致性的并行化检查方法进行了探索与研究，并行效率达到30%以上，并行加速比达到5.23。由于测试是在千兆通信网的集群环境中进行的，需考虑集群I/O的时间消耗，当进程数增加时结果受I/O影响较大，界址点与界址线拓扑检查方法的并行加速比会随着进程数的增加而有所衰减。若在高性能网络上进行测试，则无须考虑I/ O的影响。通过实验也验证了方法的可行性。将空间索引与空间数据划分方法相结合的方法为地籍数据的拓扑一致性研究与探索提供了一种研究思路，为后续的界址线与宗地、宗地与宗地之间拓扑一致性的研究提供了基础。

References)

［1］冯杭建，叶建生，许佳立.基于规则的地籍数据拓扑关系高效检测［J］.测绘与空间地理信息，2007，30(1):87-90.FENG Hangjian，YE Jiansheng，XU Jiali.Highly effective testing on topology relationship of cadastre data based on rule［J］.Geomatics＆Spatial Information Technology，2007，30(1):87-90.(in Chinese)

［2］周晓光，陈军.地籍信息系统综述［J］.地理信息世界，2006，4(3):35-40.ZHOU Xiaoguang，CHEN Jun.A survey on cadastral information system［J］.GeomaticsWorld，2006，4(3):35-40.(in Chinese)

［3］吴长彬，闾国年，舒飞跃.基于知识与规则的地籍数据质量检查方法［J］.地理与地理信息科学，2007，23(5): 22-25.WU Changbin，LYU Guonian，SHU Feiyue.Research on quality checking method based on knowledge and rule to cadastral data［J］.Geography and Geo-Information Science，2007，23(5):22-25.(in Chinese)

［4］杜波.基于“一张图”思想的城乡一体化地籍管理信息系统研究［D］.南宁:广西师范学院，2010.DU Bo.The research on urban-rural-integrated cadastral management information systems based on“amap”thought［D］.Nanning:Guangxi Normal University，2010.(in Chinese)

［5］赵春宇.高性能并行GIS中矢量空间数据存取与处理关键技术研究［D］.武汉:武汉大学，2006.ZHAO Chunyu.Studying on the technologies of storage and processing of spatial vector data in high-performance parallel GIS［D］.Wuhan:Wuhan University，2006.(in Chinese)

［6］Xavier C，Iyengar S S.Introduction to parallel algorithms［M］.USA:Wiley-Interscience，1998.

［7］冯杭建，麻土华，刘伟宏，等.地籍空间数据库拓扑关系分析及基于规则的验证方法［J］.计算机应用，2006，26(17):2522-2524.FENG Hangjian，MA Tuhua，LIUWeihong，et al.Topology relationship analysis of cadastral spatial database and validity method based on rule［J］.Journal of Computer Applications，2006，26(17):2522-2524.(in Chinese)

［8］谢忠，叶梓，吴亮.简单要素模型下多边形叠置分析算法［J］.地理与地理信息科学，2007，23(3):19-23.XIE Zhong，YE Zi，WU Liang.Polygon overlay analysis algorithm using the simple data model［J］.Geography and Geo-Information Science，2007，23(3):19-23.(in Chinese)

［9］任沂斌，陈振杰，李飞雪，等.简单要素模型多边形拓扑检查并行算法［J］.计算机应用，2014，34(7):1852-1856.REN Yibin，CHEN Zhenjie，LI Feixue，et al.Parallel algorithm of polygon topology validation for simple feature model［J］.Journal of Computer Applications，2014，34(7): 1852-1856.(in Chinese)

［10］吴立新，杨宜舟，秦承志，等.面向新型硬件构架的新一代GIS基础并行算法研究［J］.地理与地理科学，2013，29(4):1-8.WU Lixin，YANG Yizhou，QIN Chengzhi，et al.On basic geographic algorithms of new generation GIS for new hardware architectures［J］.Geography and Geo-Information Science，2013，29(4):1-8.(in Chinese)

［11］Healey R，Dowers S，Gittings B，et al.Parallel processing algorithms for GIS［M］.USA:CRC Press，1998.

［12］Liu CW，Chen H.A hash partition strategy for distributed query processing［C］//Proceedings of the 5th International Conference on Extending Database Technology，Avignon，France，1996，1057:371-387.

［13］Ghandeharizadeh S，DeWitt D J.Hybrid-range partitioning strategy:a new declustering strategy for multiprocessor databases machines［C］//Proceedings of the Sixteenth International Conference on Very Large Databases，Brisbane，Australia，1990:481-492.

［14］Zhou Y，Jiang L.Hilbert curve based spatial data declustering method for parallel spatial database［C］// Proceedings of the 2nd International Conference on Remote Sensing＆Environment and Transportation Engineering，Nanjing，China，2012:1-4.

［15］杨宜舟，吴立新，郭甲腾，等.一种实现拓扑关系高效并行计算的矢量数据划分方法［J］.地理与地理信息科学，2013，29(4):25-29.YANG Yizhou，WU Lixin，GUO Jiateng，et al.A method of spatial data partition for efficient parallel computing of topological relations［J］.Geography and Geo-InformationScience，2013，29(4):25-29.(in Chinese)

［16］Enghofer M J，Franzosa R D.Point-set topological spatial relations［J］.International Journal of Geographical Information Systems，1991，5(2):161-174.

［17］Enghofer M J，Herring J R.Categorizing binary topological relations between regions，lines，and points in geographic databases［R］.Technical Report，University of Maine，1991.

［18］李成名，朱英浩，陈军.利用Voronoi图形式化描述和判断GIS中的方向关系［J］.解放军测绘学院学报，1998，19(2):117-120.LI Chengming，ZHU Yinghao，CHEN Jun.Directional relation description and determination based on Voronoi diagram in GIS［J］.Journal of the PLA Institute of Surveying and Mapping，1998，19(2):117-120.(in Chinese)

［19］Randell D A，Cui Z，Cohn A G.A spatial logical based on regions and connection［C］//Proceedings of 3rd International Conference on Knowledge Representation and Reasoning，New York，1992:165-176.

［20］陈先伟，郭仁忠，闫浩文.土地利用数据库综合中图斑拓扑关系的创建和一致性维护［J］.武汉大学学报(信息科学版)，2005，30(4):370-373.CHEN Xianwei，GUO Renzhong，YAN Haowen.Creation and consistency maintenance of topological relationships between patches in landuse database generalization［J］.Geomatics and Information Science of Wuhan University，2005，30(4):370-373.(in Chinese)

［21］白建军，赵学胜，陈军.基于线性四叉树的全球离散格网索引［J］.武汉大学学报(信息科学版)，2005，30(9): 805-808.BAI Jianjun，ZHAO Xuesheng，CHEN Jun.Indexing of discrete global grids using linear quadtree［J］.Geomatics and Information Science of Wuhan University，2005，30(9): 805-808.(in Chinese)

［22］余接情，吴立新.球体坐标与SDOG-ESSG格网码的相互转换算法［J］.武汉大学学报(信息科学版)，2015，30(8):1116-1121.YU Jieqing，WU Lixin.Transformation algorithms between spheroid coordinates system and SDOG-ESSG grid code［J］.Geomatics and Information Science of Wuhan University，2015，30(8):1116-1121.(in Chinese)

［23］赵园春，李成名，赵春宇.基于R树的分布式并行空间索引机制研究［J］.地理与地理信息科学，2007，23(6): 38-41.ZHAO Yuanchun，LIChengming，ZHAO Chunyu.Research on the distributed parallel spatial indexing schema based on R-Tree［J］.Geography and Geo-Information Science，2007，23(6):38-41.(in Chinese)

Parallel checking method for point-line topological consistency in cadastral database

YANGYizhou1，WU Lixin1，2，GUO Jiateng1，LIU Shanjun1
(1.Institute of Geo-informatics＆Digital Mine，Northeastern University，Shenyang 110819，China；2.IoT/Perception Mine Research Center，China University of Mining＆Technology，Xuzhou 221008，China)

The current topology inspection methods which use serial computation method accompanied with the complicated algorithms and excessive calculation amount cannot satisfy the demands of the efficient topology inspection for massive cadastral data.On the basis of the characteristics of topology calculation between point and line，the parallel topological computingmethod aiming at boundary points and lines has been implemented by combining the decomposition method for boundary points data with the Q tree and R tree spatial indexmethod for boundary lines data.The topology parallel testsusing the datasets of boundary points and lines in one areawas taken in thismethod.The results show that the parallel efficiency of the algorithm which decreased with the increased number of processes steady maintains at above 30%，and the parallel speedup ratio reaches up to 5.The computation efficiency is improved more than 30 times than that of ArcGIS.Themethod can be used as a tool in high performance geographic information system and achieves good application effect.

cadastral database；topological relations；data quality；parallel computing；high performance geographic information system

P273

A

1001-2486(2015)05-040-07

10.11887/j.cn.201505007

http://journal.nudt.edu.cn

2015-06-29

国家863计划资助项目(2011AA120302)；国家自然科学基金资助项目(41001228)；中央高校基本科研业务费资助项目(N140104002)；辽宁省自然科学基金资助项目(2015020581)

杨宜舟(1987—)，男，湖北荆门人，博士研究生，E-mail:yangyizhou1987@163.com；吴立新(通信作者)，男，教授，博士，博士生导师，E-mail:awulixin@263.net