导航星座星间链路信号自适应捕获方法

2015-06-19李献斌王跃科周永彬

系统工程与电子技术 2015年1期

关键词：虚警星间时隙

李献斌，王跃科，周永彬

（国防科学技术大学机电工程与自动化学院，湖南长沙410073）

导航星座星间链路信号自适应捕获方法

李献斌，王跃科，周永彬

（国防科学技术大学机电工程与自动化学院，湖南长沙410073）

针对导航星座星间链路信号动态特性和工作特点，提出了一种基于星历辅助的自适应捕获方法。该方法利用导航卫星自有的导航电文对接收信号到达时延、多普勒频移和信噪比进行估计，根据估计结果自适应调整信号捕获的搜索范围、非相干累加次数和判决门限，以减少捕获时间、提高捕获性能。给出了自适应捕获的设计思路和流程，并结合全球定位系统真实轨道数据进行了仿真。仿真结果进一步证明了所提方法的有效性。

导航星座；星间链路；自适应；捕获；导航电文

0 引言

通过在导航卫星之间建立通信和测距链路可以使导航星座具有自主定轨功能［12］，有效提升定轨和时间同步精度［35］，实现对导航卫星自主完好性监测［-67］。为了实现不同卫星之间的数据交换与距离测量，星间链路通常采用时分体制，每条链路分配一个短暂的时隙，星座按照规划连接表进行时隙之间的切换来建立不同的链路，比如全球定位系统（global positioning system，GPS）链路中时隙长度为1．5 s［8］，Galileo系统的时隙暂时设计为0．5 s［3］。每个短暂的时隙内，要实现信号的捕获、跟踪、同步、通信和测量。因此，星间链路的建立对信号的捕获时间和捕获性能提出了较高的要求。

与此同时，导航星座的拓扑结构决定了星间信号的大动态特性。首先，卫星间高速相对运动给信号带来较大的多普勒频移；其次，星间相对距离的不同造成由信号传播带来的时延和衰减程度不同，直接决定了接收信号存在较大的时延不确定度和信噪比差异。星间链路的这种大动态特性给信号捕获带来较大的困难，与星间信号捕获性能的高要求形成了直接的矛盾。针对该问题，本文基于导航卫星自有的导航电文，提出了一种导航星座星间链路自适应捕获方法，该方法利用星历信息对信号的到达时延、多普勒频移和信噪比进行估计，根据估计结果自动调整信号捕获的搜索范围、非相干累加次数和判决门限，以减少信号的捕获时间、提高捕获性能。文中结合GPS真实轨道数据对算法的性能进行了仿真验证，并给出了结论。

1 星历辅助的捕获先验数据求解

导航星座处于一个高度精确统一的时空基准中，每颗导航卫星都存储有表征轨道信息和钟差信息的导航电文。导航电文中的星历信息包括两部分：一部分是本星的广播星历，提供米级的轨道预报精度和厘米级每秒的速度预报精度［910］；另一部分是星座内其他卫星的历书，是广播星历的简化形式，提供他星公里级的轨道预报精度和分米级每秒的速度预报精度［11］。星间链路按照统一连接规划进行切换时隙实现不同链路的连接，根据规划表可以提前获得建链开始时刻［12］。因此建链开始前可以结合星历信息求解建链时刻卫星的坐标，进而求解出信号的传输时延，多普勒频率和信噪比，为信号的捕获提供先验信息。

1.1 传输时延及其不确定度的计算

假设需要t1时刻在A、B两星之间建立星间链路，A星为主星，B星为从星。B星可根据星上导航电文中的历书信息求解出t1时刻A星的轨道坐标，包括位置和速度，分别记为向量PA（t1）和VA（t1），对应于历书精度的解算误差为ΔPA和ΔVA。假设信号t2时刻到达B星，则根据广播星历信息求解出t2时刻B星的位置和速度，记为向量PB（t2）和VB（t2），对应广播星历精度的解算误差为ΔPB和ΔVB，其中t2为未知量，则有

解方程可得t2，设传输时延τ＝t2－t1。计算时由星历误差带来的时延不确定度大小为

1.2 接收信号频率及其不确定度的计算

时延估计完成以后，得到对应的卫星A到卫星B的指向向量PAB＝PB（t2）－PA（t1）和速度向量VAB＝VB（t2）－VA（t1），VAB在PAB上的投影即为卫星B相对于卫星A的视线速度。设信号发射频率为fT，光速为c，可得接收频率为

由星历误差带来的频率不定区间为

1.3 接收信号信噪比的计算

根据链路预算［13］，由空间传播带来的信号衰减为

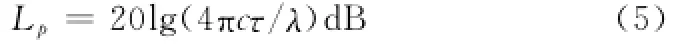
式中，λ为载波的波长。

由于卫星A天线的有效发射功率（effective isotropic radiated power，EIRP）和卫星B接收天线的增益Gr是确定的，可得接收信号的功率为

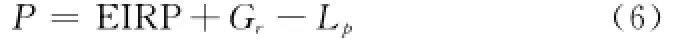
进一步可得接收信号的信噪比为

式中，k为波耳兹曼常数；N为噪声能量；Ts为接收机噪声温度；Bn为噪声带宽。

综上，基于导航电文，B星预先得到了信号的传输时延τ、接收频率fR、时延不确定度tun、频率不确定度fun和信噪比η，为信号捕获的自适应设计提供了先验信息。

2 星间链路自适应捕获方法

2.1 信号捕获流程

扩频信号的捕获是一个典型的检测与估计问题，中频信号进入捕获模块后，首先与本地载波和本地伪码进行相关运算，进行载波和伪码剥离；对相关运算后的信号进行能量累积以获得判决变量；然后将判决变量同预设门限进行比较和校验得到捕获结果，如果捕获成功，则退出捕获，否则在码相位和多普勒频移组成的二维空间上的每个搜索格点重复上述过程，判决成功时结束整个搜索过程［14］。

2.2 自适应捕获搜索范围设计

扩频信号搜索范围的大小直接决定信号的捕获时间，如图1所示，信号的二维搜索区间可用频率搜索中心位置fce、时延搜索中心位置tce、频率不定区间fun、时延不定区间tun、频率搜索步进fsp和时延搜索步进tsp组成的六维向量S来表示。

图1 捕获搜索区间特征参数

设t1时刻A、B卫星之间建链，则接收信号频率fR即为t2时刻卫星B的频率搜索中心位置fce，传输时延τ即为时延搜索中心位置tce，式（2）和式（4）求得的不确定度即为频率不定区间fun、时延不定区间tun，所以可得卫星B在t2接收时刻对应的搜索向量为

式中，fsp和tsp典型取值分别为0.67／T和tc／2，T为相干积分时间，tc为码片宽度［14］。

综上，导航星座星间链路搜索向量是信号接收时刻和参与建链卫星的函数，不同时刻、不同卫星之间建立的链路对应不同的搜索向量。

2.2.1 针对不同链路的自适应设计

针对不同链路自动调整二维搜索区间可以大大降低信号搜索范围，减小捕获时间。比如同轨道面卫星之间建立星间链路时，二者的距离变化率为零，星间信号的多普勒变化也为零，此时不需要进行频率搜索，二维搜索空间也相应地变成了一维搜索。由于相对距离不变，时延搜索范围只取决于由于星历误差带来的时延不确定度，对应的搜索向量为

该向量中的参数只是关于建链卫星的函数，而与建链时刻无关。

2.2.2 针对同一链路不同搜索次数的自适应设计

星间链路中不仅包括同轨道面之间的链路，也包括异轨道面间链路。在一个建链时隙内，异轨道面卫星间的距离和径向速度是连续变化的。

实际建链过程中，信号的捕获总存在一定的检测概率，并非每条链路进行一次二维搜索后都能成功捕获信号，特别是对于距离较长、信号空间衰减较大的链路可能需要两次或者多次二维搜索才能捕获成功。鉴于单个时隙内星间距离和距离变化率大动态特性，每次捕获相应的时延和多普勒频率也不同，从而导致搜索向量也不同，需要针对捕获次数对搜索向量进行自适应调整。

设第n次二维搜索所需时长为Tse（n），根据式（1）得到卫星B第一次捕获的时刻t2，那么对应的第n次搜索的起始时刻为

同理，根据式（1）可以得到卫星A的发射时刻t2n＋1，根据式（5）进一步求解出对应的接收信号频率。单个时隙内，频率不定区间fun、时延不定区间tun变化较小，为了简化计算，单个时隙内均取初次计算值，即

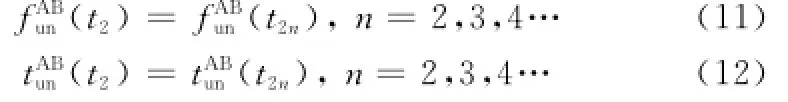
这样，就得到单个时隙内不同次数捕获构成的搜索矩阵

星间信号捕获之前，每次搜索区间的参数对照矩阵SAB中的列向量进行设置，如图2所示。

图2 单个时隙内捕获搜索示意图

2.3 自适应搜索门限设计

信号捕获成功的条件是检验统计量大于特定的门限，合理地选取捕获门限值Vt是信号捕获取得良好性能的关键一步。根据图1，经过相干累积和非相干叠加以后，检测量为

式中，Nnc为非相干累加次数；I（n）和Q（n）为经过相干积分后的信号。当有用信号不存在或者伪码完全没有对齐时，检测量V服从自由度为2Nnc的中心χ2分布，当卫星信号存在时，所得结果呈自由度为2Nnc的非中心χ2分布。对应的检测概率和虚警概率［15］分别为

式中，V*＝VtNnc／2σ2；η＝A2／（2σ）2为信噪比。

根据式（7）可以求得信号的信噪比η，联立式（15）和式（16）可以求解给定虚警概率和检测概率下的非相干积分的次数Nnc和门限Vt。

3 仿真验证

3.1 仿真场景及数据

本文以GPS为例对星间信号捕获的自适应设计进行仿真验证，所用轨道数据为国际全球卫星导航系统服务组织公布的GPS卫星2013年5月24日6时至2013年5月25日6时精密轨道数据［16］。

由于同轨道面卫星间距离变化情况较为简单，因此仿真分析时主要考虑异轨道面卫星间变化情况。根据轨道数据可得GPS卫星之间距离和距离变化率如图3所示，其中RRN28卫星的轨位是B3，PRN20、PRN22、PRN10、PRN18卫星是E轨道面的卫星。

图3 GPS PRN28卫星与PRN20＼PRN22＼PRN10＼PRN18卫星之间的距离和距离变化率变化情况

3.2 捕获搜索范围仿真分析

从图3中可以看出，异轨道面卫星间距离变化范围大，为5 444～53 231 km，对应时延不定区间为0．018 1～0．177 4 s；距离变化率较大，最高可达5．637 km／s，在一个1．5 s建链时隙内，星间距离变化可达8 km。GPS星间链路工作频段在UHF频段（250 MHz）［17］，由相对运动带来的多普勒频率区间为－4．7～4．7 KHz。

当针对单条链路进行搜索范围自适应设计时，根据式（2）和式（4），星间搜索范围的精度主要取决于星历误差。GPS导航卫星提供的广播星历中坐标精度为米级，速度精度为厘米级每秒，仿真时分别取5 m和0．05 m／s。根据历书求得的坐标精度为公里级，速度精度为分米级每秒，仿真时分别取2 km和0．5 m／s。假设星间采用1．023 MHz的码速率和1 023点的码长设计，则可得经过自适应设计前后搜索范围如表1所示。

表1 自适应设计前后捕获搜索范围对比

从表1可以看出，自适应捕获设计极大地减小了星间信号捕获的搜索范围，码相位搜索范围由1 023降为13，频率搜索范围由9．4 KHz降为1 Hz以内，从而有效减少了捕获资源，提高了捕获时间。

3.3 捕获门限和非相干积分次数仿真分析

根据星间距离变化范围，由空间传输衰减带来的功率差异最大为

此时如果不同链路均采用固定的捕获判决门限和非相干积分次数，则根据式（15）和式（16），虚警概率和检测概率的差异如图4所示。

图4 不同星间链路的捕获检测概率和虚警概率

图4 分析了星间距离变化范围从5 444 km到53 231 km依次增大的5条传输链路的捕获检测概率和虚警概率变化情况。分析时假设传输距离最短链路（5 444 km）对应的接收信号功率为110 dBmW，噪声功率密度为－205 dBW／Hz，预检噪声带宽为2．046 M Hz，相干积分时间为1 ms，非相干积分次数为1。从图4中可以看出，随着星间距离的变化，采用相同的捕获门限和非相干积分次数，不同链路的捕获检测概率和虚警概率差异较大。如图中A点和B点所示，虽然二者的虚警概率相同，均为0.2%，但检测概率分别为67．4%和29．1%；B点和C点虽然检测概率相同，但虚警概率分别为0．2%和2．51%。

根据星历信息求解出链路的信噪比，进而根据式（15）和式（16）求解出指定虚警概率和检测概率下的捕获门限和相干积分时间。以链路距离为5 444 km和10 000 km的两条链路为例进行分析，如图5中D点所示，5 444 km链路在虚警概率为0．1%时的检测概率为99．8%，为了使10 000 km的链路具有与5 444 km链路D点同样的检测概率和虚警概率，将虚警概率值（0．1%）、检测概率值（99．8%）和估计得到的信噪比带入式（15）和式（16），得到关于相干积分次数Nnc和捕获门限Vt的函数，求解方程组可得Nnc和Vt。此时求得非相干积分次数为2，捕获门限降为原来的67%。由于相干积分次数为整数，在求解时只能近似得到所要求的检测概率，如图5所示。

图5 自适应设计后的捕获检测概率和虚警概率

图5 中所示D、E、F 3点的虚警概率均为0．1%，经过非相干积分次数调整后，10 000 km链路信号的检测概率由F点的67．4%上升到E点的96．3%，基本接近5 444 km链路的检测概率，验证了算法的有效性。

4 结论

导航星座星间链路在信号传输时延、多普勒频率和接收信号功率上存在较大的动态，给信号捕获带来较大的难度，而利用导航星座特有的导航电文进行捕获初始信息求解可以有效解决信号动态大和捕获性能要求高之间的矛盾。根据星间链路工作特点和信号动态特性，本文提出一种自适应的捕获算法，针对不同链路的动态特性自适应调整捕获的搜索范围、捕获门限和非相干积分次数以达到较好的捕获性能，并结合GPS卫星真实轨道数据对算法进行了仿真验证。理论分析和仿真验证表明，通过自适应调整可以有效缩小捕获搜索范围，提高捕获的检测概率，在占用资源较少的情况下达到较好的捕获性能。

参考文献：

［1］Abusali P A M，Tapley B D，Schutz B E．Autonomous navigation of global positioning systems using cross-link measurements［J］．Journal of Guidance Control and Dynamics，1998，21（2）：321- 327.

［2］Zhang Y．Study on the autonomous navigation method based on inter-satellite measurement［D］．Changsha：National University of Defense Technology，2005．（张艳．基于星间观测的星座自主导航方法研究［D］．长沙：国防科学技术大学，2005．）

［3］Amarillo F．Inter-satellite ranging and inter-satellite communication links for enhancing GNSSsatellite broadcast navigation data［J］．Advances in Space Research，2011，47（5）：786- 801.

［4］Xu H L，Wang J L，Zhan X Q．Autonomous broadcast ephemeris improvement for GNSS using inter-satellite ranging measurements［J］．Advances in Space Research，2012，49（6）：1034- 1044.

［5］Dangelo P，Fernandez A，Guardabrazo T，et al．Enhancement of GNSS navigation function by the use of inter-satellite links［C］∥Proc.of the 6th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing，2012：1- 6.

［6］Xu H，Wang J，Zhan X．GNSS satellite autonomous integrity monitoring（SAIM）using inter-satellite measurements［J］．Advances in Space Research，2011，47（7）：1116- 1126.

［7］Rodríguez-Pérez I，García-Serrano C，Catalán C，et al．Intersatellite links for satellite autonomous integrity monitoring［J］．Advances in Space Research，2011，47（2）：197- 212.

［8］Rajan J A．Highlights of GPS II-R autonomous navigation［C］∥Proc.of the 58th Annual Meeting of the Institute of Navigation and Central Inertial and GPS Test Facility 21st Guidance Test Symposium，2002：354- 363．

［9］Guo J M，Meng X G，Li Z H，et al．Accuracy analysis of GLONASS satellite broadcast ephemeris［J］．Journal of Geodesy and Geodynamics，2011，31（1）：68- 71．（郭际明，孟祥广，李宗华，等．GLONASS卫星广播星历精度分析［J］．大地测量与地球动力学，2011，31（1）：68- 71．）

［10］Zhao L J，Zhang F Z，Cheng P，et al．Analysis of GPS broadcast ephemeris error［J］．Computer Measurement&Control，2013，21（1）：155- 157．（赵利军，张飞舟，程鹏，等．GPS广播星历的误差分析［J］．计算机测量与控制，2013，21（1）：155- 157．）

［11］Zhou S S，Wang J X．Precision compare of GPS broadcast ephemeris and almanac［J］．Journal of Geotechnical Investigation&Surveying，2006（9）：69- 74．（周善石，王解先．GPS广播星历与历书的精度比较［J］．工程勘察，2006（9）：69- 74．）

［12］Maral G，Bousquet M．Satellite communication systems：systems techniques and technology［M］．New Jersey：John Wiley＆Sons，2011．

［13］Han S，Gui Q，Li J．Establishment criteria，routing algorithms and probability of use of inter-satellite links in mixed navigation constellations［J］．Advances in Space Research，2013，51（11）：2084- 2092．

［14］Kaplan E D，Hegarty C J．Understanding GPS：principles and applications［M］．2nd ed．London：Artech House，2006．

［15］Simon M K，Omura J K，Scholtz R A，et al．Spread Spectrum Communications Handbook［M］．New York：McGraw-Hill，1994．

［16］International GNSS servive（IGS）network［EB／OL］．［2013-05- 30］．http：∥ig-scb．jpl．nasa．gov．

［17］Ananda M P，Bernstein H，Cunningham K E，et al．Global positioning system（GPS）autonomous navigation［C］∥Proc.of the IEEE Position Location and Navigation Symposium，1990：497- 508.

Adaptive acquisition algorithm for inter-satellite links in navigation constellation

LI Xian-bin，WANG Yue-ke，ZHOU Yong-bin
（College of Mechatronics Engineering and Automation，National University of Defense Technology，Changsha 410073，China）

In view of the signal dynamic characteristics and working mechanism of inter-satellite links in navigation constellation，an adaptive acquisition algorithm assisted by the navigation data is introduced．The proposed method makes use of the navigation data to calculate the time-delay，Doppler frequency and signal to noise ratio of the

signal．Based on the results，the search area，non-coherent times and threshold of signal acquisition are adjusted adaptively to reduce acquisition time while improving acquisition performance．Finally，the effectiveness of the proposed algorithm is proved by the real orbit data of the global positioning system．

navigation constellation；inter-satellite links；adaptive；acquisition；navigation data

V 448

10．3969／j．issn．1001-506X．2015．01．03

李献斌（1982-），男，博士研究生，主要研究方向为星间测距和通信技术。

E-mail：lixianbincn＠163．com

王跃科（1957-），男，教授，博士，主要研究方向为数字化测试技术。E-mail：wangyueke＠nudt．edu．cn

周永彬（1982-），男，副教授，博士，主要研究方向为信号处理与卫星导航定位技术。

E-mail：michaelzhou＠nudt．edu．cn

1001-506X（2015）01-0012-05

网址：www．sys-ele．com

2013- 06- 26；

2013- 12- 26；网络优先出版日期：2014- 03- 27。