液化天然气泄漏和水面扩散过程模拟

何思念，常华伟，文科，舒水明

（华中科技大学能源与动力工程学院，湖北 武汉430074）

引 言

LNG（液化天然气）在天然气产业和能源市场中的地位日益显著，仅2013年我国进口1700万吨LNG，而2020年则预期进口量将会达到6000万吨。LNG运输量的增加导致水上泄漏的可能性也越来越大，为了避免LNG泄漏导致的危害，对LNG泄漏过程特性的研究也越来越受到关注。当低温液体罐破裂且低温液体流出时，巨大的温差会引发快速相变 （RPT）爆炸，从而对周边设施造成损害。即使没有发生爆炸，扩散到水面或地面的低温液体会从环境中吸收大量的热，导致附近人员的冻伤，并且产生大量白雾。如果所泄漏的为可燃性物质，如LNG或液化氢 （LH2），散发到空气中的气体可能被引燃乃至发生爆炸。LNG的泄漏过程危害评估主要包括泄漏、蒸发、扩展、气体扩散和燃烧等过程［1－2］。其中，泄漏、蒸发和扩散的模拟结果是模拟可燃云扩散和建立池火模型的重要的前提条件。为了进一步提升LNG泄漏的预测模型的准确性，已经有大量的理论工作用于研究LNG在水面泄漏和扩散的可能过程和现象［3－5］。

储存在运输船中的LNG处于一个大气压的饱和状态［6］，其沸点约为－162℃，这使得LNG的储运需要采用专门的容器。储罐的结构参数、装载量及穿破位置及其孔径都会影响到泄漏总体积、持续时间及流量变化过程。漏洞孔径极大时的泄漏持续时间极短，这一过程可以视为瞬态泄漏；漏洞孔径极小时的泄漏流量几乎不随时间而变化，这一过程可以视为恒速泄漏；其他情形下的则为变流速泄漏过程。由于LNG泄漏情形的变化，LNG在水面的蒸发和扩散现象也会有很大不同。自罐中泄漏出的LNG会在水面上形成LNG液池，该池会从周围环境吸收热量并汽化成天然气蒸气。这些低温气体会形成低卧云并随风而飘移。当天然气在空气中的浓度达到可燃浓度的上下限之间并与火源接触，则可能发生剧烈燃烧或者爆炸。对于正在燃烧的LNG低温液池，低温池吸收的很大一部分热量来自于火焰的辐射传热；如果没有被引燃，则最主要的热量来自水中。同时空气被LNG池及低温气体冷却，其温度降低相对湿度增加，弥漫在空气中的水蒸气则会冷凝后产生大量白雾。

当只有少量LNG泄漏到水上，LNG将迅速汽化消失；反之，泄漏量大时，会在水面上形成低温池，池径与池深及总蒸发速率不断变化。起初LNG池迅速扩张，同时由于水的阻力而导致其扩张速度降低。对于恒速泄漏，当液池的大小与形状保持相对稳定且泄漏率等于总蒸发率时，液池便达到了平衡状态；对于瞬态泄漏，液池将会扩张到最大尺寸，之后便开始收缩或者形成环形液池；对于变流速泄漏，液池的大小始终会随泄漏率的变化而变化。液池形状还取决于堤岸与船体：如果LNG从运输船或者岸边泄漏到开阔的水域时，由于有船体和堤岸的阻挡，液面在水面的形状就近似为半圆；如果没有阻挡来限制液池扩展，则其形状将接近圆形。由于重力及蒸发作用，池深在从源点向半径扩展的方向上总体呈现出减小的趋势，但不会低于一个最小值，这一最小值由表面张力决定。

关于低温液体的泄漏的研究，目前多为国外学者的工作，国内科研人员在相关方面研究为数不多［7－9］。

早在1972年，当石油被广泛运输时，Fannelop和Waldman即提出浅水理论来研究原油的泄漏与扩散过程［10］。该模型将液池简化为圆柱体，其半径的增加由下式给出

式中，Δ＝ρLNG／ρw。

由于这一式子中只考虑了重力，因而这一模型被称为重力模型。Fay成功地将这一模型应用于LNG扩散过程的模拟中［11］，此后这一模型得到了广泛的发展和使用［12－13］。为了将扩散过程中的阻力考虑在内，Webber［14］发展出了基于浅水理论的平均深度模型。Webber的模型将池深描述为积分形式，因而在本文中将其简称为积分模型。积分模型的数值求解过程相对简单，具有良好的理论基础，它得到了广泛的使用与推广［15－17］。虽然积分模型在LNG泄漏过程的仿真建模中使用广泛，但其缺点在于，使用平均高度来简化液池的高度曲线后，池深的不均匀性被忽略了。为了更准确地描述池深及速度变化，改进后的浅水模型采用微分形式来表示质量守恒与动量守恒定律［18］。为了便于描述，在本文中改进后的浅水模型被称为微分模型。

从已有的文献资料可以看出，虽然已经有了很多学者关注于LNG泄漏相关研究，但泄漏时及其随后的现象的很多细节仍需要大力研究。首先，几乎所有文献中的模拟方案都采用恒速泄漏或瞬态泄漏，对泄漏细节描述得很少。其次，仅有的考虑了变化的泄漏速率的数据都是基于立方形储罐的。本文将模拟LNG储罐水面泄漏的情形，并给出更多相关细节，为此建立了一种基于微分模型并整合了各种储罐的计算方法。首先采用使用该计算方法来计算不同孔径下的泄漏与扩散过程，然后将MOSS储罐与立方形储罐二者泄漏后的扩散过程相比较，最后还分析讨论了LNG液池的形状。

1 数学模型和计算方法

1.1 LNG储罐结构

目前的LNG运输船主要有两种类型：MOSS和GTT储罐。MOSS型LNG储罐是标准球形，由铝合金制成。如图1（a）所示，它采用了立式提升技术 （VST）来扩展容量。忽略泵塔与其他一些内部结构的体积，MOSS储罐的横截面积可以表示为

GTT膜储罐的横截面通常为八角形，如图1（b）所示。忽略泵塔与其他一些内部结构的体积，其横截面积可以表示为

图1 LNG储罐的结构Fig.1 Construction of LNG tanks

如果简化为立方形储罐，其横截面积At则为常数。

1.2 LNG泄漏过程

当储罐被穿破后，LNG在重力作用下会泄漏出来，其流率为

其中Cd的推荐值在0.6～0.7之间［19］。

LNG液面下降速率等于源流率除以横截面积：

1.3 LNG水面扩散过程

LNG在水面扩散时，其圆形的扩散行为可以用与质量守恒和动量守恒相关的微分方程来描述。

连续性方程：

动量守恒方程：

式中，r为径向坐标；h和u分别为当地池深和平均深度径向速度；v为液体蒸发率，v＝q／ρLiL；w为LNG向水中泄漏的流率，它与总泄漏流量Q的关系为

1.4 模拟策略

图2展示了对LNG泄漏过程进行模拟分析的策略。首先是选择低温液体的种类，包括LNG、液氢和液氮等低温液体。然后是选择泄漏模型，这里共有3种模型：瞬态泄漏、恒速泄漏、储罐泄漏。根据选择会有3种不同的计算模型分别运行。其中瞬态泄漏只需设置泄漏总量。在恒速模型中需要将泄漏速率设置为常量。储罐泄漏模型中的泄漏速率根据储罐类型和装载量以及泄漏孔径来计算得出。在这3种模型中，储罐模型是最复杂也是最准确的。接下来设置泄漏模型的技术参数、初始条件和液池形状数。计算完离散方程后，输出不同时间步长的h和u还有高度剖面。还可以输出液池半径随时间变化关系曲线。

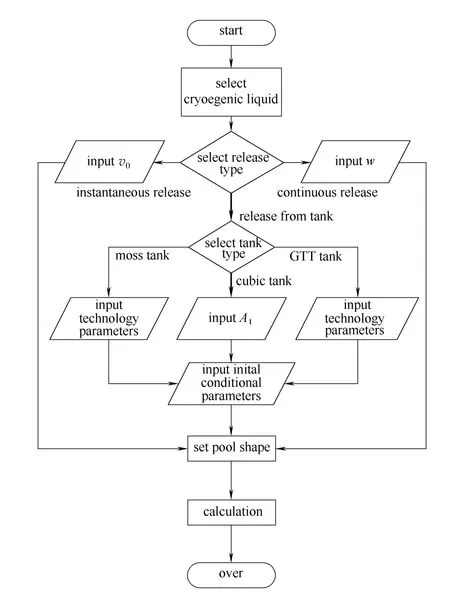
图2 模拟流程图Fig.2 Framework chart of simulation

1.5 数值计算方法

对微分方程进行求解，采用一阶有限差分显式离散格式和交错网格法。将时间步长设置为1ms，网格间距为0.05m，通过C＋＋语言编程来进行求解。低温液体的热力学参数由REFPROP提供。本文采用Verfondern等［20］的液氢在水池中扩散蒸发试验验证差分浅水方程对预测低温液体在水面扩散问题的可行性。

图3是5L·s－1的速率泄漏的LH2在水面扩散液池的半径随着时间变化情况。从图中可以看出，LH2一旦泄漏后就迅速扩散。在达到峰值后，液池就处于动态平衡中。图3中所显示出的实验与仿真结果的吻合说明了此方法的可行性。

2 模拟结果与讨论

2.1 LNG水面泄漏的基本参数

假设有12500m3LNG从立方形储罐中通过直径1m的孔洞泄漏出来，并在水上形成一个半圆形LNG池。

图3 液氢扩散实验和模拟结果对比图Fig.3 Validation of numerical results for spreading of liquid hydrogen with experimental results

LNG性质：

成分：甲烷

密度：422.5kg·m－3

潜热：510.82kJ·kg－1泄漏参数：

容积：25000m3

排放口系数：0.65

储罐类型：立方体

横截面积：961.5m2

总泄漏量：12500m3

孔径：1m

孔以上液体初始高度：13m

液池形状：半圆形

LNG水面换热热通量：85kW·m－2

图4显示了LNG池在泄漏伊始迅速扩散，之后液池开始萎缩至全部蒸发，在第341秒时池径达到峰值108m。通过方程 （1）知，当LNG泄漏到水面上时，其在重力作用下迅速横向扩散。图4中的趋势线清楚地描述了随着池深逐步减小，LNG的扩散速率也在降低。当LNG池达到最大时，泄漏流量与蒸发流量二者近似平衡：

随着储罐内的液面越来越低，LNG的泄漏流量也越来越小，液池半径也就随着时间逐渐减小，直至完全消失。

图5中显示了计算所得的最大LNG池的池深及平均高度曲线。开始时池深迅速减小，而后稳定在0.1m左右。在R＝30m处存在一个波峰，之后池深随着半径的增大不断减小到0。深度平均值为0.0873m，其标准偏差为0.1005m。当LNG在水上扩散时，由于蒸发与重力作用，其深度通常会变小但是当其速度大于当地深度处的重力波的速度时，会发生水跃，使得高度截面突然上升［21］，影响液池蒸发和扩散过程。

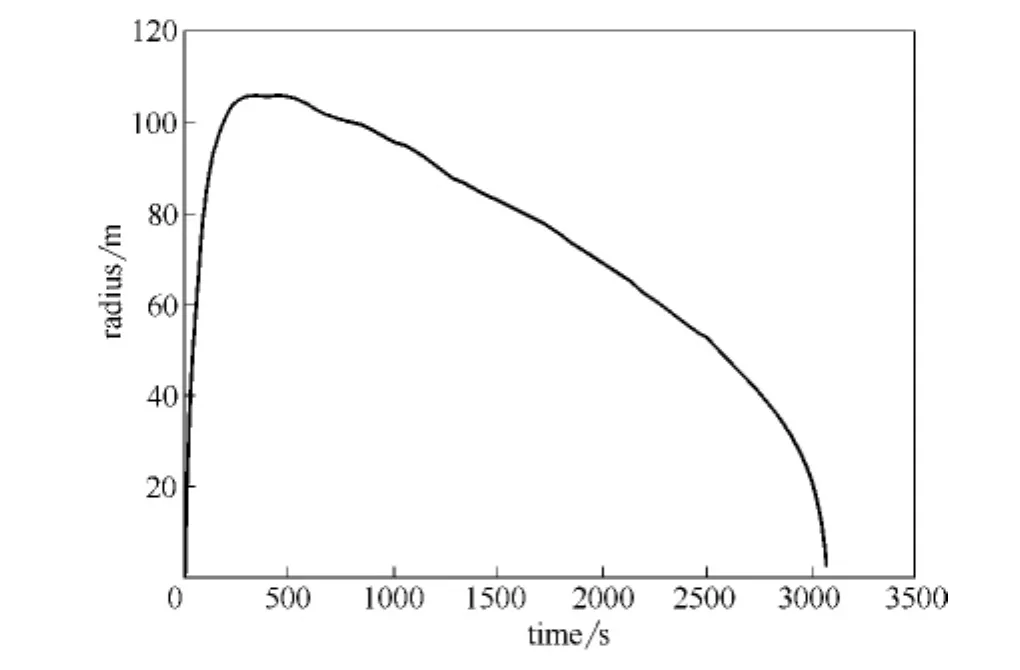
图4 12500m3 LNG从孔径为1m的储罐中泄漏后水面扩散半径计算结果Fig.4 Calculated result of pool radius for 12500m3 LNG releasing from a 1mdiameter breach hole

图5 LNG液池在341s时的高度曲线Fig.5 Height profile of LNG pool at 341s

2.2 漏洞孔径对LNG扩散过程的影响

改变基本情形下的泄漏口直径，保持其他条件不变，重新计算这一系列的泄漏过程。从图6中能够看出，随着漏洞孔径增加，微分模型计算的最大池径与积分模型的计算结果有着相同的变化趋势，最大半径跟漏洞孔径呈现相似的Boltzmann非线性关系，即随着孔径增加，最大液池尺寸也急剧增加，当泄漏孔径达到5m时，液池半径稳定至一个渐进值。但这两个模型结果的渐近值不同，微分模型的渐近值约为265m，而积分模型的渐近值约为350m。Qiao等［19］的长期瞬态泄漏理论很好地解释了这一现象。然而从图中可以看出，采用积分模型和采用微分模型得到的渐近线之间存在差异。可以推断液面高度曲线的不均匀性导致了微分模型和平均深度积分模型计算结果之间明显的差异。

图6 分别采用微分模型和积分模型模拟LNG从不同孔径泄漏过程Fig.6 Calculation of LNG pool behavior of LNG spilling from various hole of different size with intergral model and differential model.

2.3 LNG从MOSS储罐中泄漏的扩散过程

一个标准LNG船的载运量为1×105～2×105m3，每个船内含4～6个储罐。这里研究的是内置圆柱型体积为25000m3的MOSS储罐，其主要的技术结构参数列在表1中。除了储罐的技术结构参数外，其余所有计算条件都与基本情形保持一致。表2表示了MOSS储罐与立方形储罐的LNG泄漏后的扩散过程特性。从表2所显示的结果中可以看出，MOSS储罐的最大池半径比立方形储罐大1m，但池存在周期则少14s。

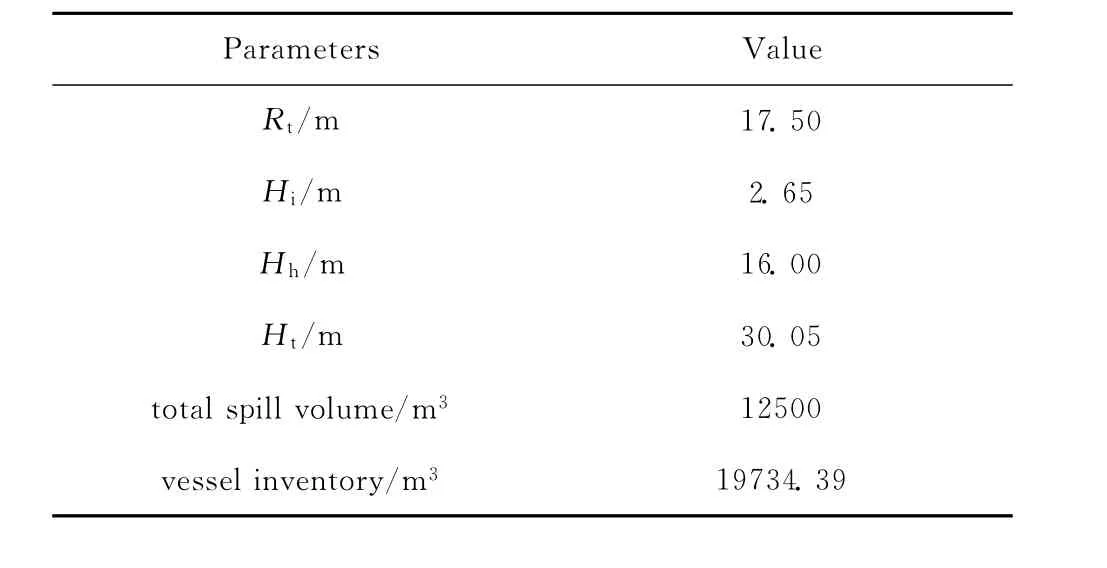
表1 容积为25000m3的MOSS LNG储罐的主要技术参数Table 1 Main technical parameters of 25000m3 MOSS LNG carrier

表2 LNG从MOSS储罐和立方体储罐泄漏的模拟结果Table 2 Computated results for LNG release from MOSS spherical tank and cubic tank

基于式 （5）可知，当液压头相同时，储罐横截面积越小则液面降低越快。由于MOSS储罐的横截面积随深度而变化，其LNG泄漏率的变化与立方形储罐的泄漏率变化不一致，流量的不同变化会影响到LNG在水面的扩散过程。不过，从表2可以看出，MOSS储罐和立方形储罐的泄漏过程的差别并不是很大，其中影响最大的是达到最大扩散半径的时间，其相差也不过2%，而最大半径以及池寿命相差都在1%之内。由此可以得出，在要求不高的情形下，用立方形储罐替代其他不规则形状的储罐也是可行的。

2.4 液池形状对LNG扩散的影响

如图7所示，因船身的阻挡，LNG池的形状在圆形与半圆形之间变化。一般情况下，液池形状总体上近似为半圆形，少部分情形下则近似于圆形。表3表征了分别采用半圆形和圆形液池来模拟液池扩散过程的结果。结果表明，半圆形液池的最大半径是圆形液池的1.385倍 （约等于），这说明两种形状下的液池最大面积几乎相同。从表中还可以看出，液池的生命周期也几乎相同，但由于船体的阻挡，液池扩散速度相对较慢，这就导致使用半圆形液池达到最大直径的时间比圆形的晚了71s。

图7 LNG在水面扩散俯视图Fig.7 Top view of LNG spreading on water

表3 采用圆形和半圆形液池的计算结果Table 3 Computational results with semicircle and circular pool

3 结 论

LNG运输船泄漏是一个比较危险而且较复杂的物理过程。在众多的危害预测模型中，浅水微分模型相对更复杂和准确。本文选择浅水微分模型对泄漏过程中的各种影响因素进行了评估，并对比了积分模型和微分模型的结果。结果表明，在LNG扩散的过程中，液池会形成阶跃，由此导致液池高度曲线与平均值的离线度达到1.15。由于考虑了液池高度的不均匀，微分模型计算的液池半径比积分模型的要小。但两者的泄漏孔径的影响趋势是严格一致的Boltzmann非线性关系。通过计算MOSS储罐发现，采用标准立方体储罐来替代MOSS等不规则储罐来对LNG的泄漏扩散过程进行模拟是合理的。最后，对比圆形和半圆形液池扩散过程发现，船体的阻挡会减缓扩散过程，但对液池的最大扩散面积的几乎没有影响。

符 号 说 明

Ap——液池面积，m2

At——LNG上表面面积，m2

a0～a2，b0，b1，l——GTT储罐基本结构参数，m

Cd——泄漏系数，1

d——距离，m

F——摩擦力，kg

g——重力加速度，m·s－2

Hh——泄漏孔高度，m

Hi——垂直加高高度，m

Ht——LNG在储罐内高度，m

h——液池高度，m

¯h——平均高度，m

R——液池半径，m

Rt——MOSS储罐的半径，m

r——半径，m

Q——体积流率，m3·s

t——时间，s

u——速度，m·s－1

Vp——液池体积，m3

v——单位面积汽化速率，m·s－1

w——源项，m·s－1

Δ——相对密度，1

ρLNG——LNG密度，m3·kg－1

ρw——水的密度，m3·kg－1

［1］ Saraf S，Melhem G.Modeling LNG pool spreading and vaporization／／Proceedings of the AIChE Spring Meeting，ioMosaic Corporation ［C］.Atlanta，GA，2005.

［2］ Woodward J L，Pitbaldo R.LNG Risk Based Safety：Mode－ling and Consequence Analysis ［M］.New York：John Wiley ＆Sons，2010.

［3］ Fay J A.Model of spills and fires from LNG and oil tankers［J］.JournalofHazardousMaterials，2003，96 （2）：171－188.

［4］ Lehr W，Simecek－Beatty D.Comparison of hypothetical LNG and fuel oil fires on water ［J］.JournalofHazardous Materials，2004，107 （1）：3－9.

［5］ Pitblado R，Baik J，Hughes G，Ferro C，Shaw S.Consequences of liquefied natural gas marine incidents ［J］.Process SafetyProgress，2005，24 （2）：108－114.

［6］ Spaulding M L，Swanson J C，Jayko K，Whittier N.An LNG release，transport，and fate model system for marine spills ［J］.JournalofHazardousMaterials，2007，140（3）：488－503.

［7］ Zhang Lijing （张礼敬），Ding Li（丁立），Tao Gang （陶刚）.Simulation of accident consequences of liquefied chlorine pipeline leakage ［J］.JournalofChemicalIndustryand Engineering（China）（化 工 学 报 ），2008，59 （5）：1333－1337.

［8］ Liu Zhongliang（刘中良），Luo Zhiyun （罗志云），Wang Jieteng（王皆腾），Zhang Jian （张建），Sun Xiaochun （孙晓春）.Analytical calculation of leakage rate for natural gas pipelines ［J］ .JournalofChemicalIndustryand Engineering（China）（化 工 学 报 ），2008，59 （8）：2121－2126.

［9］ Pan Xu （潘旭），Jiang Juncheng （蒋 军 成）.Research on discharging dispersion of chemical dangerous gases and its influence factors ［J］.JournalofNanjingUniversityof ChemicalTechnology（南京化工大学学报），2001，23（1）：19－22.

［10］ Fannelop T K，Waldman G D.Dynamics of oil slicks ［J］.AmericanInstituteofAeronauticsandAstronautics Journal，1972，10 （4）：506－510.

［11］ Fay J A.Spread of large LNG pools on the sea ［J］.Journal ofHazardousMaterials，2007，140 （3）：541－551.

［12］ Ivings M，Lea C，Webber D，Jagger S，Coldrick S.A protocol for the evaluation of LNG vapour dispersion models［J］.JournalofLossPreventionintheProcessIndustries，2013，26 （1）：153－163.

［13］ Parihar A，Vergara C，Clutter J K.Methodology for consequence analysis of LNG releases at deepwater port facilities［J］.SafetyScience，2011，49 （5）：686－694.

［14］ Webber D.Source terms ［J］.JournalofLossPreventionin theProcessIndustries，1991，4 （1）：5－15.

［15］ Brambilla S，Manca D.Accidents involving liquids：a step ahead in modeling pool spreading，evaporation and burning［J］.JournalofHazardousMaterials，2009，161 （2／3）：1265－1280.

［16］ Subramani A，Jayanti S，Shet U S P，Selvaraj P.Dynamics of liquid sodium pool spreading under sodium fire conditions［J］.NuclearEngineeringandDesign，2009，239 （7）：1354－1361.

［17］ Khajehnajafi S，Pourdarvish R.Correlations for mass transfer from a liquid spill：comparisons and recommendations ［J］.ProcessSafetyProgress，2011，30 （2）：178－184.

［18］ Verfondern K，Dienhart B.Pool spreading and vaporization of liquid hydrogen ［J］.InternationalJournalofHydrogen Energy，2007，32 （13）：2106－2117.

［19］ Qiao Yuanhua，West H H，Mannan M S，Johnson D W，Cornwell J B.Assessment of the effects of release variables on the consequences of LNG spillage onto water using FERC models［J］.JournalofHazardousMaterials，2006，130（1／2）：155－162.

［20］ Verfondern K，Dienhart B.Experimental and theoretical investigation of liquid hydrogen pool spreading and vaporization［J］.InternationalJournalofHydrogenEnergy，1997，22（7）：649－660.

［21］ Raj P K.Evaporating liquid flow in a channel （an integral model based on shallow water flow approximation）［J］.JournalofLossPreventionintheProcessIndustries，2011，24（6）：886－899.