运用多点地质统计学确定水下分流河道宽度及钻遇概率

向传刚

（中国石油大庆油田有限责任公司勘探开发研究院，黑龙江 大庆163712）

0 引言

大庆长垣南部下白垩统姚一段葡I 油层组，为一套三角洲前缘相沉积体系，以水下分流河道砂沉积为主，具有河道窄小、横向变化快等特点［1］，对河道宽度的描述是该类储层构型研究的难点［2-3］。储层随机建模技术的快速发展及地质统计学的理论更新与油田开发需要密切相关［4-7］。1962年，法国著名学者Matheron 提出了地质统计学，在其后的发展中，随机模拟技术逐步成熟完善［8］。近年来，人们广泛应用随机模拟方法进行储层非均质表征［9-10］。然而，地下储层本身具有不确定的性质和特征，在资料不完善的条件下，人们对河道等微相几何特征的认识还存在不确定性。作为一项油藏建模新技术［11］，多点地质统计学综合了传统建模方法的优点，用“训练图像”代替变差函数，刻画地质体复杂的空间结构与几何形态，最大程度地加入先验的地质知识，在描述空间变量的连续性和变异性方面具有较好的优势［12-13］。而采用了序贯算法，较易忠实井信息，并具有便捷、快速等特点。本文以大庆长垣南部某三角洲前缘相沉积区块为例，探讨应用多点地质统计学和对子井资料确定水下分流河道宽度的方法，其结果有一定的指导意义，可为储层精细非均质性研究提供参考。

1 多点地质统计学的优势

确定性建模，主要是先将密井网精细沉积相研究成果进行数字化处理，然后直接赋值给模型，最后生成确定性模型。该方法的优点是沉积相分布遵从理想化的沉积模式，缺点是河道宽度等参数依赖于人为的推测。基于两点地质统计学的沉积相随机模拟，主要用变差函数建立某方向两点之间参数变化关系，随机模拟沉积相的分布。

从三角洲前缘相平面分布来看，水下分流河道有窄小、弯多的特点。对于依据变差函数的两点地质统计学方法来说，其模拟结果不能很形象地反映水下分流河道的弯曲、摆动及连续性，而多点地质统计学在描述空间变量的连续性和变异性方面具有较好的优势［12-13］，这为水下分流河道的宽度研究提供了新方法。

2 水下分流河道随机模拟

本次研究以大庆长垣南部某三角洲前缘相沉积区块为试验区，结合多个位置点对子井钻遇水下分流河道的情况，进行了多点地质统计学水下分流河道随机模拟和概率统计研究。

2.1 研究区地质概况

研究区油藏属于白垩系姚家组一段的葡Ⅰ油组，共分为11 小层和26 个沉积单元，为一套三角洲前缘沉积的砂泥岩交互地层。砂体以水下分流河道沉积为主，部分为席状砂，厚度大于2.00 m 的单砂体钻遇率仅为15.1%，而厚度小于1.00 m 的钻遇率高达61.3%，平均单砂层厚度为0.85 m，是典型的窄薄砂岩油藏。该油组储层非均质性较强，描述水下分流河道在平面上的发育规模是开展该类油藏非均质性研究的关键。

2.2 训练图像的建立

在常规两点地质统计学中，主要通过变程作为控制条件来模拟参数分布。对于多点地质统计学沉积相模拟来说，训练图像起着控制作用。训练图像是三维沉积相模拟的基础［12-13］，用来体现地质人员想要模拟的典型沉积相几何分布形态。在建模软件中，训练图像可以通过3 种方式得到： 一是用布尔模型在规则的网格上建立一个简单的无条件3D 模型；二是地质人员根据其理想的沉积相模式和井震结合结果进行手工画相；三是外部导入模型（如3D 数字露头模型）。本研究根据区块沉积背景及现代沉积研究结果，结合井震预测结果，采用手工画相的方法建立训练图像（见图1）。

图1 不同宽度条件下水下分流河道沉积微相训练图像

训练图像源本为油田某二次加密井区92 单元，区内河道钻遇率为32.3%，与整个研究区的81-92 单元河道钻遇率接近。区内储层属于葡I 油组沉积时期，物源方向为NNE。对其沉积微相研究表明，河道砂体呈弯曲条带状，剖面呈顶平底凸透镜状。依据密井网的测井资料横向对比，基本可以确定河道的走向，但水下分流河道的边界在井间的具体位置无法确定。绘制相带图时，依据经验将河道边界定为1/2 井距处。目前井网为300 m×300 m 九点法面积井网，局部钻有二次加密井。据此统计沉积相带图中河道宽度范围为100～200 m。参考鄱阳湖三角洲水下分流河道的发育规模［13］，认为河道宽度范围为50～200 m 较为合理。

本文在建立训练图像时，根据研究区的沉积背景及现代沉积研究成果，再结合井震预测结果，分别在水下分流河道宽度为40，80，120，160，200 m 情况下，以人机交互方式，建立了水下分流河道训练图像。这样，既能反映区内水下分流河道定性分布模式，又可为多点地质统计学随机模拟提供基础模型。

2.3 地质模型的建立

多点地质统计学相模拟方法，最初模拟是在一些粗的网格上进行的，然后逐渐细化。模拟过程中，可以用第2 变量数据体作为约束条件，进行协同随机模拟。本次研究采用密井网区波阻抗属性体作为第2 变量，对沉积微相进行约束，采用多点地质统计学随机模拟的方法，建立水下分流河道沉积相模型。

从模拟结果（见图2）来看，应用多点地质统计学，能较好地反映不同宽度河道在平面上的相对位置关系。模拟结果考虑了河道宽度的不确定性问题，再现了研究区81-92 单元不同水下分流河道宽度条件下弯曲、多分岔、砂体横向变化快的特点。该结果模型，既忠实于井信息，又实现了训练图像的结构性，因此具有较高的可靠性。

图2 不同训练图像条件下沉积微相随机模拟结果

3 水下分流河道宽度分析

由于开发区存在一部分对子井，可以在不同河道宽度训练样本条件下的模拟结果上再虚拟一些对子井，通过统计其钻遇河道的概率情况，然后与实际对子井资料进行对比，从而确定水下分流河道的常见宽度。

3.1 虚拟对子井设置

区内基础井网为300 m×300 m 的规则井网，根据实际对子井分布情况，对基础井网的每口井分4 个方向设置了8 口50 m 井距的虚拟更新井（见图3），与原实钻井配对成8 对虚拟对子井。在进行概率统计时，每个对子井方向的2 口虚拟更新井，每次只允许1 口与对应实钻井进行配对，统计其钻遇河道的情况。即N 与O 井配成对子井统计其钻遇情况时，S 井不参与统计。

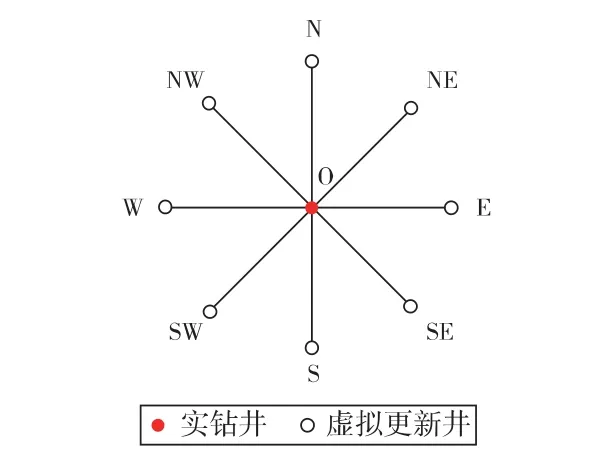
图3 虚拟对子井设置示意

3.2 对子井钻遇水下分流河道情况

研究区内目前尚无小井距密井组，不能采用密井组解剖提取法确定河道的宽度。但区内存在99 对井距为50 m 左右的对子井，本次研究对这些对子井的水下分流河道钻遇情况进行了统计。以区内水下分流河道较为发育的81-92 单元为例，通过对99 口对子井的沉积微相研究，按结果分4 种方向进行统计（见表1）。结果表明，若对子井钻遇河道，NS 向对子井钻遇同一河道的比例较高，其次为近NE—SW 向对子井，这与沉积区物源方向为NNE 向的认识一致。

表1 研究区所在油田不同方向对子井钻遇分流河道情况

3.3 水下分流河道宽度概率分布

采用不同训练图像和100 个随机种子，对研究区水下分流河道各进行了100 次的随机模拟，分别统计不同对子井方向的水下分流河道钻遇情况的概率 （见表2）。由表2可知，钻遇率数据与平均钻遇率具有一定的标准偏差，这说明河道钻遇情况具有不确定性。但是，河道宽度为120 m 和160 m 时，标准偏差较小，一般小于0.2，其结果较为可信。通过与实际对子井钻遇情况对比，发现河道宽度在120 m 时，虚拟对子井钻遇情况的钻遇率平均值与实际钻遇概率基本一致。同时由钻遇概率分布（见图4）可以看出，各向的虚拟对子井钻遇率基本呈正态分布，其结果遵循统计学原理。

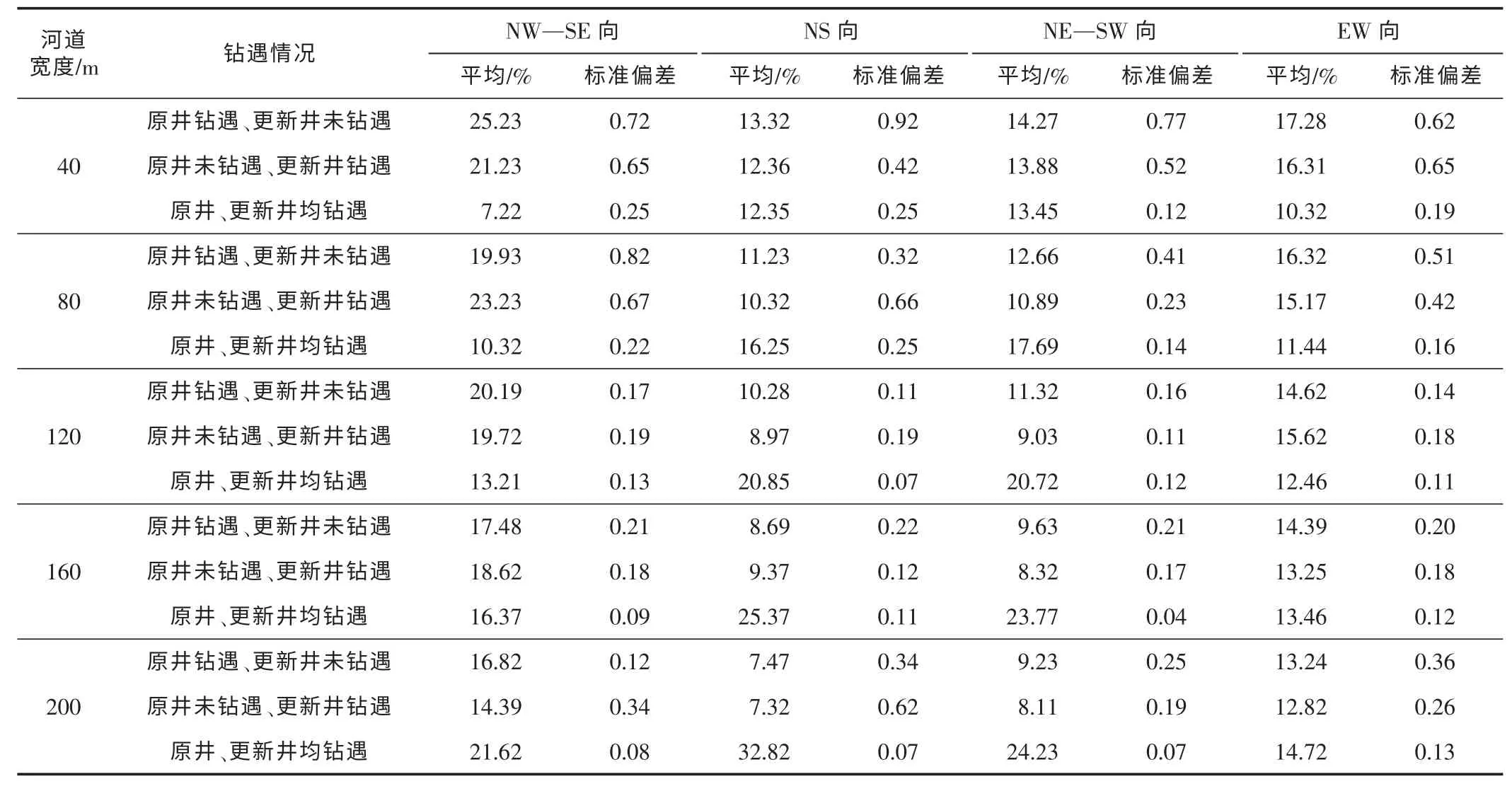
表2 不同训练图像条件下100 次随机模拟钻遇率

从地质上对该区块开展了井震结合预测研究，主要以波阻抗反演指导绘制井震结合相带图为主。通过提取该区块井震结合预测结果，河道宽度基本定为80～150 m，以120 m 河道宽度居多。其结果与本次研究较为符合，因此可以确定研究区内河道宽度为120 m。

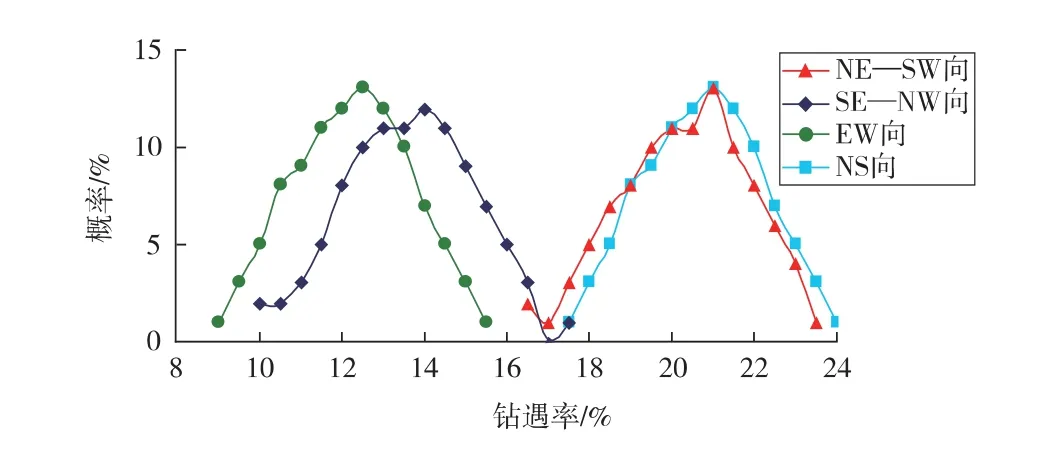
图4 120 m 河道宽度时各向对子井均钻遇同一河道概率分布

4 结论

1）运用多点地质统计学，以“训练图像”代替变差函数，可以模拟刻画地质体复杂的空间结构与几何形态。在三角洲前缘相沉积区，采用不同河道宽度制作“训练图像”，可对水下分流河道进行精细描述，包括河道的平面形态描述及不同井网钻遇微相组合概率统计，有助于指导油田开发中制订更加合理的开发方案。

2）根据基础井网中每口井4 个方向虚拟对子井钻遇河道的情况，利用多点地质统计学随机模拟结果与对子井钻遇河道的钻遇情况进行对比，可以确定河道的宽度，为储层精细非均质性研究提供了基础。

［1］林承焰，余成林，董春梅，等.老油田剩余油分布：水下分流河道岔道口剩余油富集［J］.石油学报，2011，32（5）：829-834.

［2］赵翰卿，付志国，吕晓光.储层层次分析和模式预测描述法［J］.大庆石油地质与开发，2004，23（5）：74-77.

［3］陈婷婷，胡望水，李相明，等.从密井网区到探评井区沉积微相平面图的编制［J］.断块油气田，2014，21（5）：545-549.

［4］李玉君.相控下的流动单元三维建模研究［J］.断块油气田，2007，14（6）：47-49.

［5］江艳平，芦凤明，李涛，等.复杂断块油藏地质建模难点及对策［J］.断块油气田，2013，20（5）：585-588.

［6］尹艳树，冯舒，尹太举.曲流河储层建模方法的比较研究［J］.断块油气田，2012，19（1）：44-46.

［7］李伶俐，何生，马伟竣.随机建模在大牛地气田新区早期气藏描述中的应用［J］.断块油气田，2010，17（3）：280-284.

［8］Journel A G，Huijbregts C J.Mining geostatistics［M］.London-New York-San Francisco：Academic Press，1978：21-26.

［9］宁士华，肖斐，束宁凯.特高含水开发期曲流河储层构型深化研究及应用［J］.断块油气田，2013，20（3）：354-358.

［10］Kostenevich K A.Construction of detailed 3D geological model of a deposit with difficult geological structures on the basis of basic facies models［R］.SPE 136422，2010.

［11］吴胜和，李文克.多点地质统计学：理论、应用与展望［J］.古地理学报，2005，7（1）：137-143.

［12］石书缘，尹艳树，冯文杰.多点地质统计学建模的发展趋势［J］.物探与化探，2012，36（4）：655-660.

［13］段冬平，侯加根，刘钰铭，等.多点地质统计学方法在三角洲前缘微相模拟中的应用［J］.中国石油大学学报：自然科学版，2012，36（2）：22-26.