平流层软式飞艇的多参数敏感性分析

李天娥，孙晓颖，陆正争，2，武 岳，王长国（.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），50090哈尔滨；2.中国航天建设集团，0007北京；.哈尔滨工业大学复合材料与结构研究所，5000哈尔滨）

平流层软式飞艇的多参数敏感性分析

李天娥1，孙晓颖1，陆正争1，2，武 岳1，王长国3
（1.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），150090哈尔滨；
2.中国航天建设集团，100071北京；3.哈尔滨工业大学复合材料与结构研究所，150001哈尔滨）

为研究各参数对平流层软式飞艇力学性能的影响，采用基于拉丁超立方抽样的全局灵敏度分析方法——Sobol'法对某平流层软式飞艇进行了多参数敏感性分析，统计分析了材料参数、荷载参数及外形参数对结构静力性能及自振特性的总体敏感度；采用单参数变化的思想，研究了主要敏感参数对结构最大等效应力、最大变形及自振频率的影响规律.结果表明：对于结构静力性能，蒙皮面密度及吊索相关参数的敏感度可以忽略不计；对于自振特性，吊索相关参数的敏感度可以忽略不计；增加长细比、蒙皮厚度、蒙皮弹性模量或减小径向最低点压差值可以有效地提高结构的局部力学性能；增加径向最低点压差值或减小长细比可有效提高结构腰部抗变形能力.

平流层飞艇；多参数敏感性；Sobol'法；拉丁超立方抽样；振动

平流层飞艇是长时间驻留在20 km高度左右的一种浮空器.长时定点驻空的特点使平流层飞艇成为新型的信息平台，在航空探索、地面监测、通信通讯等领域备受青睐［1］.由于平流层大气密度小、气压低，所以平流层飞艇体积一般都很庞大.软式飞艇以其可满足大体积、轻质要求的特征，成为平流层飞艇的首选结构形式［2］.

平流层软式飞艇属于大尺度太空充气膜结构.但不同于建筑膜结构，为了满足长时定点驻空的要求，平流层飞艇对其受力性能有着严格的精度要求.然而在结构加工中，存在着众多影响结构性能的不确定因素，如材料性能、内外压差值及几何外形等.这些因素与设计值的随机误差导致实际结构与设计模型间存在一定的误差.实际结构加工中，不可能完全消除这些因素的不确定性.所以，需要通过参数敏感性分析确定不同参数对飞艇结构力学性能的影响程度，为合理控制不同参数的随机误差，提高飞艇结构的设计精度提供参考.

敏感性分析包括单参数敏感性分析与多参数敏感性分析［3］.单参数敏感性分析是在其他参数不变的情况下，分析单个参数对目标性能的影响程度，称为局部敏感度.该方法已经在结构工程领域得到了广泛的应用，但在飞艇领域的应用还较少.姚伟等［4］从飞行器控制角度出发，采用单参数敏感性的思路分析了地理纬度、抗风能力、有效载荷重量、蒙皮材料比重等参数对飞艇优化尺寸的影响.单参数敏感性分析方法操作简单，但无法考虑参数间的耦合作用，且对于非线性较大的模型，得到的参数敏感性会受到其余参数中心取值的影响［5］.

多参数敏感性分析考虑了参数间的相关性，结果更加科学、合理.国外对多参数敏感性的研究主要集中在生态、医学领域［6］.近年来，国内相关学者将其引入结构工程领域.陈旭［7］采用Sobol'法分别研究了单层柱壳和K6型网壳中屋面恒荷载、杆件截面积、风荷载输出响应等参数对结构最大位移、杆件最大内力的影响，定量地描述了这些参数的一阶敏感度、交叉项敏感度和总敏感度.程军［8］等采用Sobol'法研究了环形张力索桁架结构中构件长度误差对构件的截面积、单元初始预应力、初始长度、弹性模量的敏感度.Zdenek［9］采用Sobol'法分析了单层平面钢架结构承载能力对材料属性以及几何特性等重要初始随机缺陷的敏感度.平流层软式飞艇具有结构复杂、非线性强、参数众多的特点，故采用多参数敏感性分析方法［7－9］更为合理.

综上所述，国内外尚缺少对平流层飞艇的参数敏感性研究，尤其是多参数敏感性分析.本文以某旋转椭球飞艇为研究对象，建立了含有艇体、吊索、吊舱、尾翼的分析模型，对其进行了静力及自振工况下的多参数敏感性分析，且分析了主要结构参数对结构静力性能及自振频率的影响规律，为指导结构设计提供了重要依据.

1 多参数敏感性分析

1.1 Sobol'法

多参数敏感性分析是在所有参数同时随机变化的情况下，研究参数及参数间相互作用对结构性能的影响程度，称为全局敏感度.多参数敏感性分析方法主要包括回归法［10］、响应面法［11］、Morris法［12］、傅里叶幅度法［13］、Sobol'法［14］、傅里叶幅度敏感度检验扩展法（EFAST）［15］.其中，Sobol'法与EFAST法对非线性较强、参数相互作用较明显及参数较多的模型有很好的适用性.但是，EFAST法的分析模型必须赋予整数频率的独立参数、计算较为复杂、结果收敛较慢、算法稳健性较差［7］.本文采用Sobol'法，该方法可分析参数1次，2次及更高次敏感度，可区分参数独立及交叉项的敏感度. Sobol'法的核心思想是将参数对模型的总方差分为参数的独立方差及参数间相互作用的方差.假设模型Y＝f（x），x＝x1，x2，..，xk，xi服从［0，1］均匀分布.该模型可分解为［16－18］记x）d x＝f0，对除了xi外的所有参数积分得fi（xi），对除了xi、xj外的所有参数积分得i，xj），以此类推，可得f1，2，..，k（x1，x2，..，xk）.所有参数对模型结果的影响程度表示为V＝）d x－f02；单个参数对模型结果的影响程度表示为Vi＝d xi；参数间的作用对模型结果的影响程度表示为Vi1，i2，...，is＝xi1d xi2..d xis.它们间存在的关系为

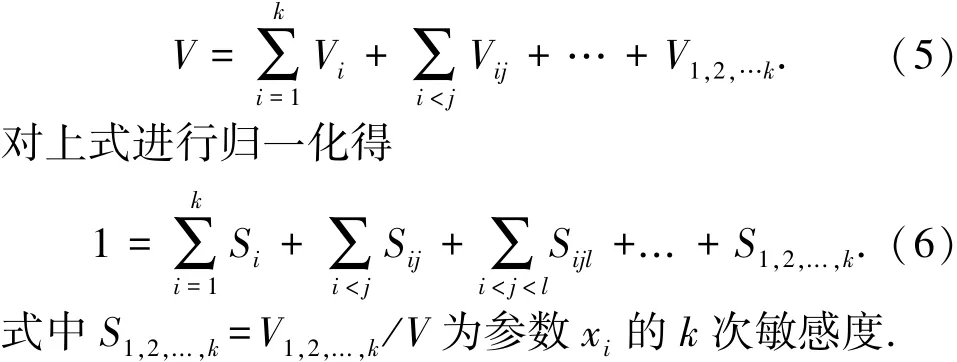
参数xi的敏感度等于所有包含参数xi的敏感度之和，即STi＝∑S（i）.

对于参数较多的敏感度计算，将分析参数分为两组来简化计算.假设分析参数有4个，令v＝x1，u＝（x2，x3，x4）.则参数x1的总体敏感度由下式计算：式中，vj，uj和v′j，uj为两次抽样的样本，N为每次抽样的样本数量.

1.2 拉丁超立方抽样

多参数敏感性分析之前需要通过抽样获取参数样本.本文采用拉丁超立方抽样（LHS），该方法是传统蒙特卡洛采样法的改进［17］.LHS利用较少的抽样次数即可较好地获取覆盖参数定义空间的样本.与一般抽样法相比，LHS的抽样效率提高约20%～40%［5］.

LHS的具体操作为：首先按照等概率分层方法对总体样本空间进行分段划分，在划分的小区间内等概率抽样；其次在子区间内采用映射法生成随机数.例如对于函数Y＝f（x1，x2，…，xn），在第i个区间的随机数xi可以通过下式得到［16］：

式中：x为［0，1］内均匀分布的随机数；xi为第i个子区间的随机数，满足（i－1）／N＜xi＜（i／N），i＝1，2，..，N，即xi能均匀分布在所有子区间内.

2 分析模型

2.1 有限元模型

平流层软式飞艇结构主要由提供浮力的流线形艇体、载荷的吊舱、起稳定控制作用的尾翼组成.本文对某软式飞艇进行足尺建模，其艇体为双椭球体，如图1所示［18］.艇体两个长半轴及短半轴的基准值分别为a1＝59.5 m、a2＝84.0 m、b＝20.5 m.采用十字形尾翼，单片尾翼尺寸如图2所示.

图1 双轴椭球体飞艇横截面

图2 单片尾翼尺寸

吊索的布置方式如图3所示，设3排共15根.吊索的直径d＝5 mm；弹性模量EC＝120 GPa.图3中的矩形为吊舱，设其尺寸为长15.0 m×宽5.5 m×高3.0 m.

图3 吊索的布置图

采用ANSYS进行建模，艇体蒙皮采用Shell181单元，吊索采用Link10单元，模型尾部固定，头部允许X向变形.

2.2 分析参数

分析参数包括蒙皮厚度、蒙皮弹性模量、蒙皮面密度、吊索直径、吊索弹性模量、吊索长度误差、径向最低点压差值及长细比.径向最低点压差值为y＝－b对应位置的内外压差，现代软式飞艇径向最低点压差值的估算公式为P0＝(125+0.033 V2max)N／m2，其中Vmax（km／h）是最高空气速度［2］.文献［19］给出20 km处的风速一般为10～25 m／s（对应P0＝167.8～392.3 Pa），文献［20］给出20 km处的最大风速为28 m／s（对应P0＝460.3 Pa）.Vmax的具体取值与飞艇的工作环境有关，本文假定P0基准值为400 Pa，样本取值范围为360～440 Pa；长细比为艇体的纵向长度与径向最大直径的比值.

进行多参数敏感性分析前，采用LHS对参数进行两次样本抽样.假设所有参数服从均匀分布，各参数的抽样范围及标准值见表1.

表1 参数分布及抽样范围

3 多参数敏感性分析

3.1 静力多参数敏感性分析

飞艇承受的主要静荷载包括艇体自重、吊舱荷载及浮力.艇体自重按照面荷载施加，设艇体蒙皮的体密度为432 g／m3［21］；吊舱荷载以集中力的方式施加，按每1 000 m3艇囊体积对应10～13 kg的悬挂系统进行计算［2］；浮力以梯度压差的形式作用于艇体，沿艇体径向不同高度处的压差按照下式计算［22］：

式中：h为荷载施加点所在平面与艇体最大截面最低点的距离；y、b分别为荷载施加点的纵坐标及艇体的最大半径值；P0为艇体最大截面最低点的压差值；ρa0＝1.189 3 kg／m3，ρhe0＝0.169 kg／m3分别为常温下空气和氦气的密度；g＝9.8 m／s2为重力加速度.

假设各参数取标准值得到的结构性能为基准态.参数发生变化时，对应的结构性能会与基准态发生偏离.采用应力与变形的差异描述偏离的趋势与程度.应力与变形的差异通过误差均方根表示：

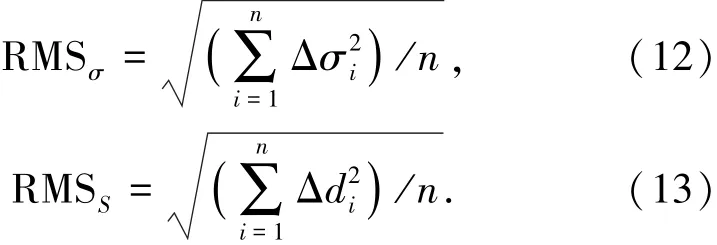
式中：RMSσ，RMSS分别为应力与变形误差均方根；Δσi为分析状态点的应力与基准态对应点应力差值；Δdi为分析状态点与基准态对应点之间的距离；n为结点数.

本文除了分析各参数随机变化对RMS的总体敏感度，还分析了对结构最大等效应力σmax与最大变形δmax的总体敏感度.其中RMS反映结构的整体力学性能，σmax与δmax反映结构的局部力学性能.

样本数较少时，各参数敏感度的波动较大.当样本数达到一定数目后，各参数敏感度逐渐趋于稳定.图4以RMSS为例，给出了各参数敏感度随样本数量的变化曲线.当样本数达到1 200时，各参数敏感性基本达到稳定.

图4 RMSS对各参数的敏感度稳定性曲线

计算RMSσ、RMSS、σmax及δmax对各参数的敏感度，如图5至图8所示.为了从整体上对不同类型参数的总体敏感度进行比较，对计算所得的敏感度进行归一化处理.

由图5、图6发现，RMSσ及RMSS对λ、P0及Tm的敏感度都比较大；由于弹性模量反映的是材料的变形能力，所以RMSS对Em的敏感度达到22.34%，而RMSσ对Em的敏感度却可以忽略不计；与主要敏感参数相比，RMS对蒙皮面密度及吊索相关参数的敏感度约等于0，说明蒙皮面密度及吊索相关参数的变化对结构整体静力性能的影响可以忽略不计.

图5 RMSσ对各参数的敏感度

图6 RMSS对各参数的敏感度

图7 σmax对各参数的敏感度

图8 δmax对各参数的敏感度

由图7与图8发现，对于反映结构局部力学性能的σmax与δmax来说，λ、P0、Tm都为主要敏感参数，蒙皮面密度及吊索相关参数为不敏感参数.δmax对参数Em的敏感度达到了53.02%，但σmax对参数Em的敏感度却可忽略不计.

对比图5～8发现：在静力作用下，飞艇结构整体力学性能与局部力学性能对蒙皮面密度及吊索相关参数的敏感度都可以忽略不计.对于反映结构应力性能的RMSσ与σmax，主要敏感参数为λ、P0、Tm；对于反映结构变形性能的RMSS与δmax，除上述三参数外，Em的影响不可忽略.

基于多参数敏感性分析结果，计算分析了主要敏感参数对结构最大等效应力与最大位移的影响规律，如图9～12所示.

图9 σmax和δmax随λ的变化

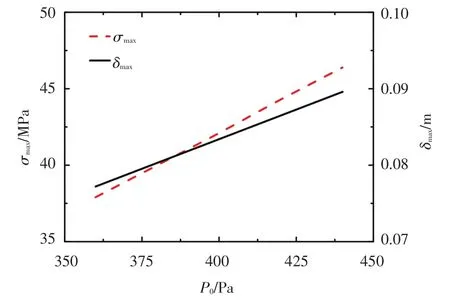
图10 σmax和δmax随P0的变化

图11 σmax和δmax随Tm的变化

图12 σmax和δmax随Em的变化

由图9发现，随着长细比λ的增加，σmax与δmax都呈线性减小的趋势；由图10发现，随着径向最低点压差值P0的增加，σmax与δmax都呈线性增加的趋势.由图11发现，随着蒙皮厚度Tm的增加，σmax与δmax都呈线性减小的趋势；图12表明δmax随着蒙皮弹性模量Em的增加而减小，σmax随Em的增加而发生微小的下降.

参数变化规律分析结果说明在满足设计要求的前提下，增加λ、Tm、Em或减小P0可以有效地减小结构应力集中与位移集中的局部极值，提高结构的局部力学性能.

3.2 自振特性的多参数敏感性分析

在参数取基准值时，对飞艇结构进行振动分析，前12阶的自振频率列于表2.

表2 前十二阶自振频率

由表2发现，飞艇结构的前六阶频率接近于0，这是由于飞艇结构处于无约束、无外荷载的飘浮状态，根据结构力学，结构的前六阶振型主要表现为刚体模态，主气囊没有明显的变形，结构整体发生振动.列举结构的第三阶模态与第五阶模态如图13（a）与13（b）所示.结合表2与图13发现，软式飞艇具有重频的现象.其中，第7阶与第8阶的频率接近，振型类似，振型为不同方向的压扁；第9阶与第10阶频率接近，振型为不同方向的腹部截面十字收缩；第11阶与第12阶频率接近，振型为不同方向的弯扭.

由图13发现，从第七阶开始，飞艇结构的艇体腰部出现大的变形，且随着模态阶数的增加而增加.从第11阶模态开始，结构腰部发生较大变形的同时还伴随着整体的弯扭变形.因此，在结构设计时，要特别注意飞艇腰部的设计，且应该注意提高结构的整体抗弯及抗扭性能.

分析各阶频率对各参数的敏感度，归一化后的结果列于表3.

图13 前12阶模态

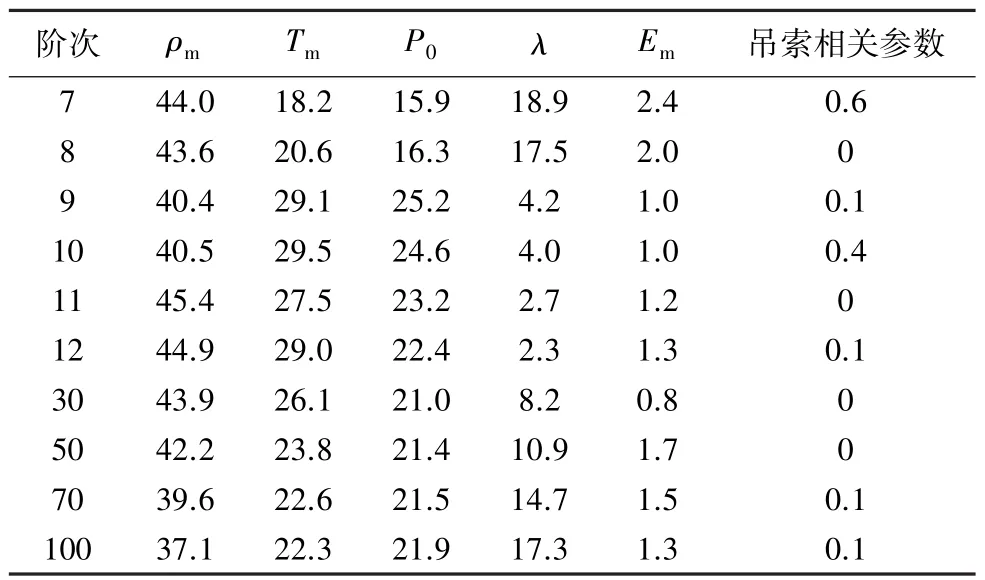
表3 不同阶次对各参数的敏感度%

观察表3的7～12阶次发现，相邻阶次的各参数敏感度相近，该现象亦可由各参数对结构各阶自振频率的影响曲线斜率得以验证（如图14～18所示）.综合观察表3发现，由于结构的自振频率与自重、刚度直接相关，所以体现结构自重的蒙皮面密度ρm、蒙皮厚度Tm及体现结构刚度的径向最低点压差值P0、长细比λ为自振频率的主要敏感参数，其中ρm的影响最大，Tm与P0的敏感度接近，λ的敏感度随着阶次显示先减小后增大的趋势；与主要敏感参数相比，蒙皮弹性模量Em的敏感度相对较小；吊索相关参数的敏感度很小，可以忽略不计.

由图14～18发现，软式飞艇的相邻振动阶次具有明显的重频现象，且相邻阶次的频率随各参数的变化趋势相同及斜率相近.由图14发现，随着蒙皮面密度ρm的增加，结构自重增加，对应各阶频率都呈现降低趋势；同理，各阶频率随蒙皮厚度Tm的增加亦呈现降低趋势（如图15所示）.由图16发现，随着径向最低点压差值P0的增加，第7～12阶频率明显增加，这是由于结构刚度随着P0的增加而增加，即提高了结构抗弯扭变形及腰部抗压变形能力.由图17发现，随着长细比λ的增加，第7（8）阶频率及11（12）阶频率具有降低的趋势，而第9（10）阶频率变化较小，说明结构的腰部抗变形能力及抗弯扭刚度随着λ的增加而降低.

综上，增加P0或减小λ可以有效的提高结构的刚度，即提高结构腰部抗变形能力.

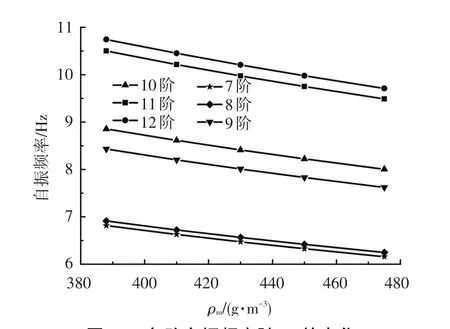
图14 各阶自振频率随ρm的变化

图15 各阶自振频率随Tm的变化

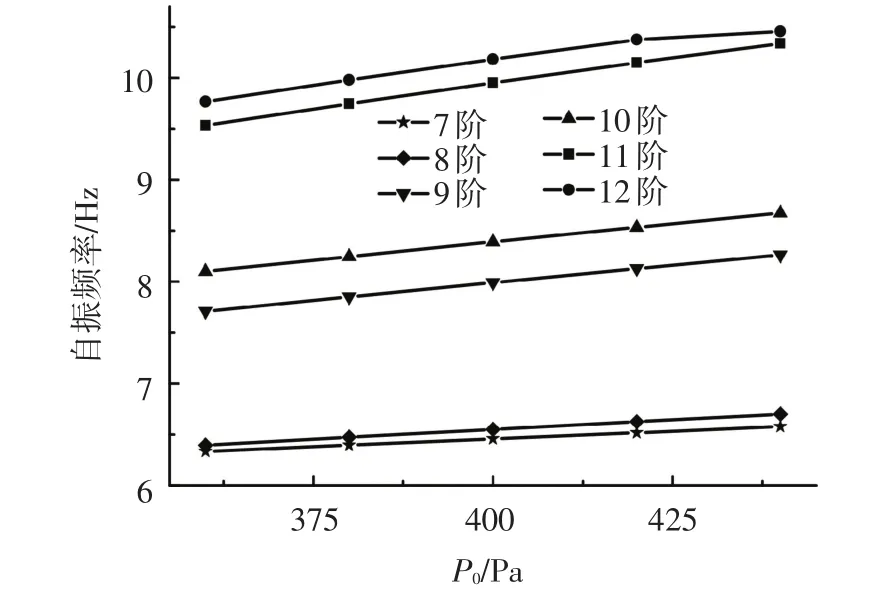
图16 各阶自振频率随P0的变化

图17 各阶自振频率随λ的变化

4 结 论

本文对平流层软式飞艇进行了静力性能与自振特性的多参数敏感性分析，分析了主要敏感参数对结构最大等效应力、最大位移及自振频率的影响，得到如下结论：

1）长细比、径向最低点压差值、蒙皮厚度是影响结构应力性能的主要参数；除上述参数外，影响结构变形性能的主要参数还包括蒙皮弹性模量；蒙皮面密度及吊索相关参数对结构静力性能的影响可忽略不计.

2）蒙皮面密度、蒙皮厚度及径向最低点压差值、长细比为自振频率的主要敏感参数；相比主要敏感参数，蒙皮弹性模量对自振频率的影响较小；吊索相关参数对自振频率的影响可忽略不计.

3）增加长细比、蒙皮厚度、蒙皮弹性模量或减小径向最低点压差值可有效地减小结构应力集中与位移集中的局部极值，提高结构的局部力学性能.

4）结构的振动具有重频特点.结构设计时，要特别注意提高飞艇腰部的抗变形能力.增加径向最低点压差值或减小长细比可有效提高结构腰部抗变形能力.

［1］BORMANNA，HERRMANN J P，SKUTNIK S.Alternative buoyancy concepts：Firstnumericaland experimentalresults from a hot steam balloon［C］／／AIAA′s 3rd Annual Aviation Technology，Integration，and Operations（ATIO）Forum.Reston VA：AIAA，2003：AIAA 2003－6840.

［2］KHOURY G A，GILLETT J D.Airship technology［M］. Cambridge：Cambridge University Press，1999.

［3］张晓航.防空导弹武器装备体系作战效能全局敏感性分析方法研究［D］.长沙：国防科学技术大学，2010.

［4］姚伟，李勇，王文隽，等.平流层飞艇优化方法和设计参数敏感性分析［J］.宇航学报，2007，28（6）：1524－1528.

［5］金晓飞.500米口径射电望远镜FAST结构安全及精度控制关键问题研究［D］.哈尔滨：哈尔滨工业大学，2010.

［6］徐崇刚，胡远满，常禹，等.生态模型的灵敏度分析［J］.应用生态学报，2004，15（6）：1056－1062.

［7］陈旭.单层网壳结构风振响应参数灵敏度研究［D］.哈尔滨：哈尔滨工业大学，2012.

［8］程军.柔性预张力结构的构件长度误差敏感性分析［D］.浙江：浙江大学，2010.

［9］ZDENEK K.Sensitivity analysis of stability problems of steel plane frames［J］.Thin⁃Walled Structures，2011，49：645－651.

［10］MANACHE G，MELCHING C S.Identification of reliable regression and correlation⁃based sensitivity measures for importance ranking of water⁃quality model parameters［J］. Environmental Modeling and Software，2008，23（5）：549－562.

［11］SANAYEI M，IMBARO G R.Structural model updating using experimental static measurements［J］.Journal of Structural Engineering，1997，123（6）：792－798.

［12］MORRIS M D.Factorial sampling plans for preliminary computational experiments［J］.Technometrics，1991，33（2）：161－174.

［13］LU Yichi，MOHANTY S.Sensitivity analysis of a complex，proposed geologic waste disposal system using the fourier amplitude sensitivity test method［J］.Reliability Engineering and System Safety，2001，72（3）：275－291.

［14］SOBOL'I M.Sensitivity analysis for non⁃linear mathemati⁃cal models［J］.Mathematical Modelling and Computational Experiment，1993，1：407－414.

［15］SALTELLI A，TARANTOLA S，CHAN K P S.A quantitative model⁃independent method for global sensitivity analysis of model output［J］.Technometrics，1999，41（1）：39－56.

［16］陆正争.软式飞艇参数敏感度分析与优化［D］.哈尔滨：哈尔滨工业大学，2013.

［17］贾建芳，岳红，王宏.基于LHS方法NF⁃κB信号转导网络的多参数敏感性分析［J］.应用基础与工程科学学报，2008，16（4）：605－615.

［18］MUELLER B J，MICHAEL A P，ZHAO Yiyuan. Development of an aerodynamic model and control law design for a high⁃altitude airship［C］／／AIAA 3rd Unmanned Unlimited Technical Conference.Reston VA：AIAA，2004：20－23.

［19］邓黎.平流层飞艇的环境控制［J］.航天返回与遥感，2006，27（3）：51－56.

［20］王永志，张卫民，王斌，等.高空飞艇阻力计算［C］／／中国第一届近代空气动力学与气动热力学会议论文集.绵阳：中国空气动力学会，2006：882－885.

［21］曹旭，顾正铭，王伟志.可用于平流层飞艇蒙皮的PBO织物编织和性能研究［J］.航天返回与遥感，2008，28（3）：57－62.

［22］席俊波.飞艇囊体几何非线性有限元分析［D］.西安：西北工业大学，2006.

（编辑 张 宏）

Multi⁃parameter sensitivity of stratosphere non⁃rigid airship

LI Tian′e1，SUN Xiaoying1，LU Zhengzheng1，2，WU Yue1，WANG Changguo3
（1.Key Lab.of Structural Engineering and Control（Harbin Institute of Technology），Ministry of Education 150090 Harbin，China；2.China Aerospace Construction Group Co.，Ltd，100071 Beijing，China；3.Center for Composite Material and Structure，Harbin Institute of Technology，150001 Harbin，China）

In order to study the influence of parameters on mechanical performance of stratosphere non⁃rigid airship，Sobol'method which is a global sensitivity analysis method based on the Latin hypercube sampling is used for analyzing the multi⁃parameter sensitivity.The global sensitivities of material parameters，load parameters and configuration parameters to the static performances and the vibration characteristics are analyzed.The influence laws of the main sensitive parameters on the maximum equivalent stress，the maximum deformation and frequencies are analyzed based on the single parameter changing.The research indicates that the sensitivities of membrane surface density and sling parameters to the static performances can be neglected.The sensitivities of sling parameters to the vibration characteristics can be neglected.Local mechanical properties can be effectively improved by increasing slenderness ratio，membrane thickness，membrane elastic modulus or decreasing pressure at the radiallowestpoint. The anti⁃deformation capacity of waist can be effectively improved by increasing the pressure at the radial lowest point or decreasing slenderness ratio.

stratosphere airship；multi⁃parameter sensitivity；Sobol'method；Latin hypercube sampling；vibration

V274

A

0367－6234（2015）10－0013－07

10.11918／j.issn.0367⁃6234.2015.10.003

2014－09－11.

国家自然科学基金（50908068，91215302）；航空科学基金（2013ZA77001）.

李天娥（1987—），女，博士；武 岳（1972—），男，教授，博士生导师；王长国（1979—），男，教授，博士生导师.

孙晓颖，sxy_hit＠163.com.