界面点源和半圆柱在直角域中的反平面散射

高 春，齐 辉，潘向南，蔡立明，赵元博（.哈尔滨工程大学航天与建筑工程学院，5000哈尔滨；2.哈尔滨学院土木工程系，50086哈尔滨）

界面点源和半圆柱在直角域中的反平面散射

高 春1，2，齐 辉1，潘向南1，蔡立明1，赵元博1
（1.哈尔滨工程大学航天与建筑工程学院，150001哈尔滨；2.哈尔滨学院土木工程系，150086哈尔滨）

为得到直角域中垂直边界上的半圆柱对点源载荷的反平面弹性动力学解析解，按照镜像方法和波函数展开法，研究了点源对半圆柱的稳态散射以及其与边界的相互作用，得到直角域中的位移场和应力场.首先，延拓直角域为半空间，延拓半圆柱为圆柱，得到等价问题；其次，构造位移波的波函数级数表达式；最后，对圆柱边界做Fourier展开，定解波函数系数.数值计算了圆柱边沿的动应力，结果表明，半圆柱的散射总是明显地分为投射侧和隐蔽侧，相对低频总是能引起更大的动应力，介质参数对径向动应力和周向动应力的分布，有着截然不同的影响.理论分析得到的稳态解丰富了SH波散射的理论，为双相介质界面圆柱的SH波散射的Green函数方法奠定了基础，数值算例为相应的工程问题提供了参考.

SH波散射；点源函数；界面圆柱；直角域；动应力分布

反平面运动作为弹性动力学最简单与最基本的研究对象，具有十分重要的理论意义.作为反平面弹性动力学问题的SH波传播与散射在地震工程、岩土工程、地下工程等中有着广泛的应用价值.早在上世纪七、八十年代，文献［1－2］就已经系统地研究了SH波对柱体的散射问题.本世纪以来，文献［3－10］陆续研究了全空间中界面圆孔、圆柱、衬砌对平面SH波和反平面线源荷载的散射，文献［10－11］研究了SH波入射下，凸起结构与不同基础地形的相互作用.近年来，文献［12－19］分别研究了弹性直角域和双相介质中圆柱孔洞、夹杂对SH波和点源荷载的散射，并且取得了一定成果.但双相介质半空间中界面圆柱的反平面散射问题的相关研究还很匮乏，鉴于界面动力学问题的复杂性和重要性，本文研究界面反平面点源荷载对弹性直角域中的界面圆柱的稳态作用.这是解决双相介质界面圆柱对SH波散射的Green函数方法的基础，利用本文构造的界面点源荷载的稳态解，通过叠加原理就可以求得任意分布的界面荷载对含界面半圆柱的弹性直角域的稳态响应.同时，通过对数值算例进行的分析，本文得到的结论可以为理论研究和工程实践提供一定的参考和指导.

1 描述与分析

1.1 控制方程

本文研究一类弹性动力学反平面问题.如图1所示，有一个弹性直角域，其水平边界为BH平面，垂直边界为BV平面.在垂直边界上嵌入一个半圆柱，它的圆心O点位于BV平面上，距离水平边界BH平面的直线长度为h.直角域的剪切弹性模量为μ1，质量密度为ρ1，半圆柱的剪切弹性模量为μ2，质量密度为ρ2.以半圆柱的圆心O点为原点，垂直边界BV平面内法线方向为x轴正方向，水平边界BH平面外法线方向为y轴正方向，建立平面直角坐标系（O，x，y）.以原点O为极点，x轴为极轴，按逆时针方向，建立平面极坐标系（O，r，θ）.以出平面方向（图中标为“☉”）为反平面位移的正方向，入平面方向为反平面位移的负反向.

图1 弹性直角域中的界面点源和半圆柱

这样，弹性直角域和半圆柱中的质点分别满足波动方程

式中：Δ为二维Laplace算子，w为反平面位移，f为反平面外力.

考虑稳态问题，分离时间变量t和空间变量（x，y），（r，θ），得到位移空间变量非齐次Helmholtz方程为

式中：k1、k2分别为直角域和半圆柱中剪切波的波数；c1、c2分别为直角域和半圆柱中剪切波的相速度为略去时间谐和函数exp（－iωt）的反平面外力；ω为稳态运动的角频率.

按照复变函数描述，引入复变量z和共轭复变量－z ，建立复平面（z，，其中，i＝－1是虚数单位.

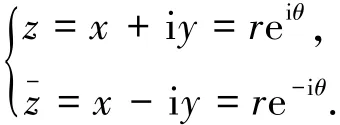
在垂直边界BV平面上的i y0点，有反平面稳态点源荷载δ（z－i y0）exp（－iωt），代入非齐次的Helmholtz方程式（1），即fω＝δ（z－i y0），它们的解分别为

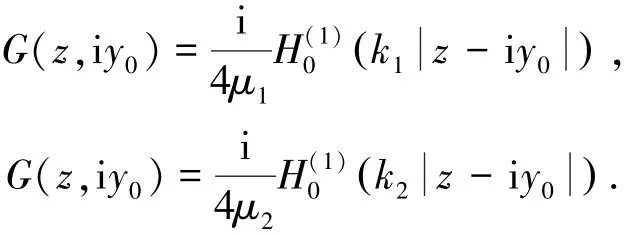
它们是点源函数在全空间中的基本解，其中，δ（·）为Dirac函数·）为0阶第1种Hankel函数.

1.2 等价问题

本文讨论的反平面弹性动力学对应的数学物理方程定解问题的泛定方程就是控制方程式（1），定解条件是BH平面和BV平面上齐次的Neumann条件以及BC柱面上齐次的Dirichlet条件和Neumann条件.

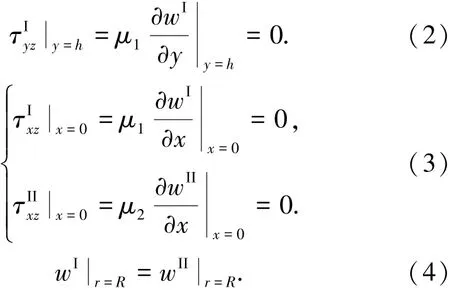
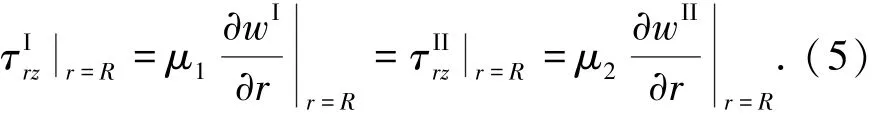
这里，应力分量和位移的上标I和II分别代表在直角域Medium I和半圆柱Medium II中.

按照镜像的方法构造定解问题的等价问题.如图2所示，以垂直边界BV平面为对称面，将直角域延拓为半空间，将半圆柱延拓为圆柱，在延拓的区域中加上对称的反平面稳态点源荷载δ（z－i y0）exp（－iωt）.按这样延拓处理，前后的定解问题完全等价，并且自然满足BV平面上的Neumann条件式（3）.

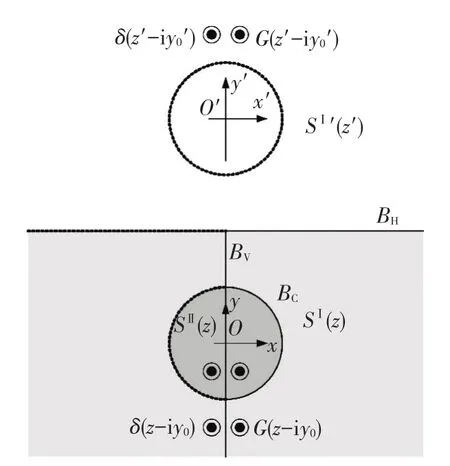
图2 等价问题的镜像方法

这是含圆柱夹杂的弹性半空间在对称面上的反平面点源荷载作用下的稳态响应问题.作为稳态问题，在以下讨论中，统一略去时间谐和函数exp（－iωt）.

2 位移波的表达式

2.1 点源荷载

等价问题的反平面外力是点源荷载2δ（z－i y0）.

当它的作用点在延拓的圆柱内，即y0＜R时，它的位移场GII以及径向应力分量τrz（记作GIrIz）为

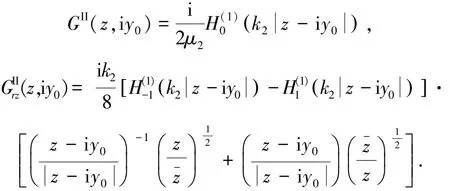
当它的作用点在由直角域延拓得到的半空间内，即y0≤h且y0≥R时，需要考虑水平边界BH平面的影响.如图2所示，在原点O关于BH平面对称的镜像点O′上，建立平面直角坐标系（O′，x′，y′），其对应的复变量z′和共轭复变量－z ′满足

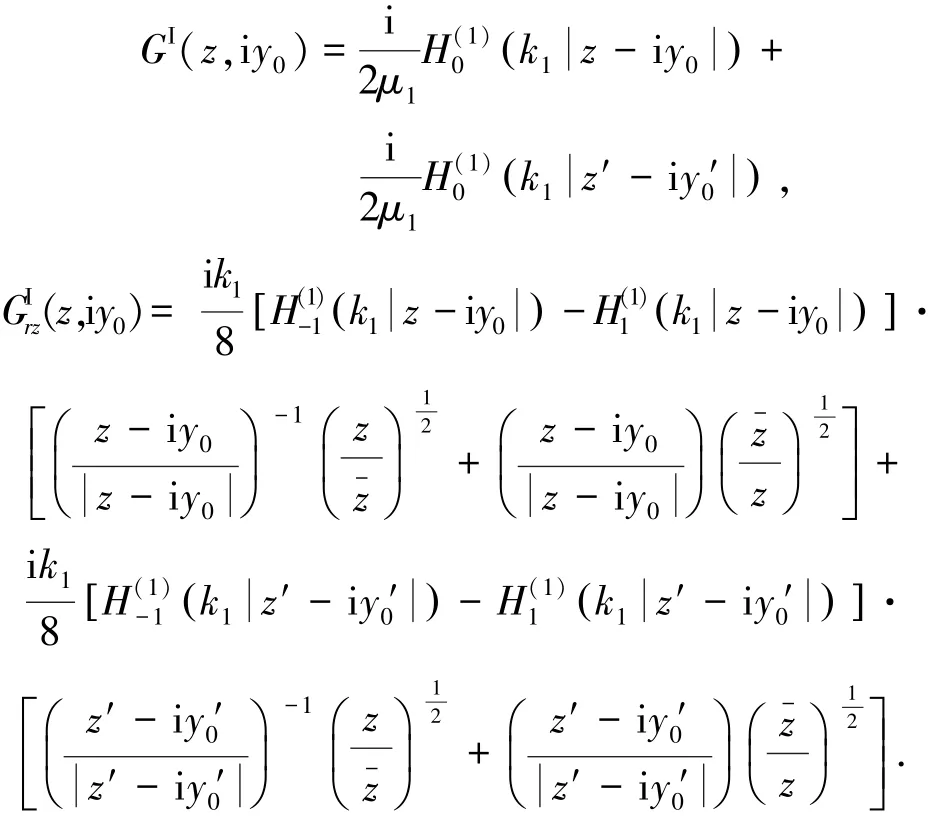
2.2 圆柱的位移波

按照Fourier⁃Hankel波函数展开法，延拓的圆柱在延拓的半空间中将会产生散射波.它的位移场记作SI，表示为级数形式为

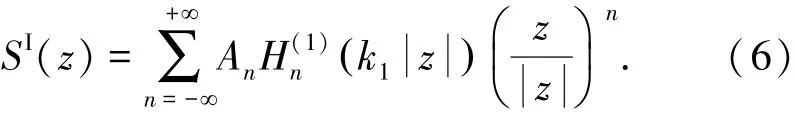
式中An为待定的波函数系数.

散射波的径向应力分量τrz记作SIrz，表示为级数形式为

式中Ｈ－ｎ（ｚ）、Ｈ+ｎ（ｚ）分别为求导得到的中间变量.

按照镜像的方法，构造延拓的圆柱关于水平边界ＢＨ 平面对称的镜像散射波.它的位移场记作ＳＩ′，它的径向应力分量τｒｚ 记作ＳＩｒ ｚ ′，它们的级数形式表示为

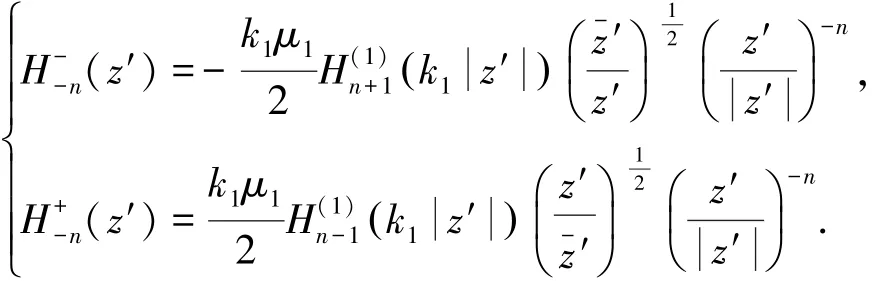
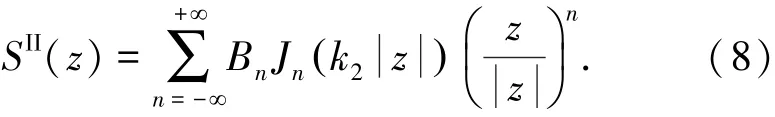
式中：Bn为待定的波函数系数，Jn（·）为n阶Bessel函数.驻波的径向应力分量τrz记作表示为级数形式为

于是，本文得到等价问题的弹性半空间和圆柱中的位移场w和径向应力分量场τrz的表达式.

3 定解方程组

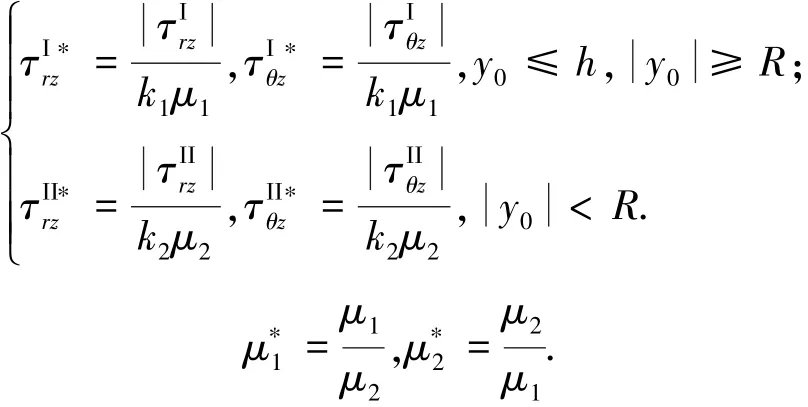
式中z ＝R，它们都是角变量θ的函数.对式（9）两端分别按角变量θ做Fourier级数展开，按照简谐函数系的正交性，得到待定系数An和Bn的线性代数方程组，截断方程组，按常规的Gauss消去法，即可求得An和Bn的具体数值.

4 延拓圆柱边沿的动应力

4.1 应力按照波函数展开法，将计算求得的An和Bn的具体数值代入Fourier⁃Hankel波函数和Fourier⁃Bessel波函数的级数式（6）～（8），加上已知的反平面外力点源荷载2δ（z－i y0），这样就得到了等价问题中的全部波场.当y0＜R时，延拓的半空间和圆柱

在等价问题中，延拓的半空间Medium I的径向应力分量场和周向应力分量场均满足：

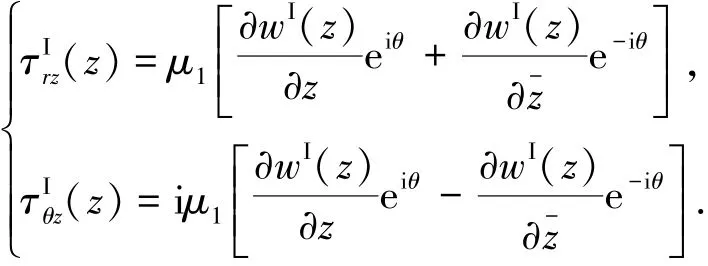
延拓的圆柱Medium II的径向应力分量场τIIrz（z）和周向应力分量场τIIθz（z）圴满足：

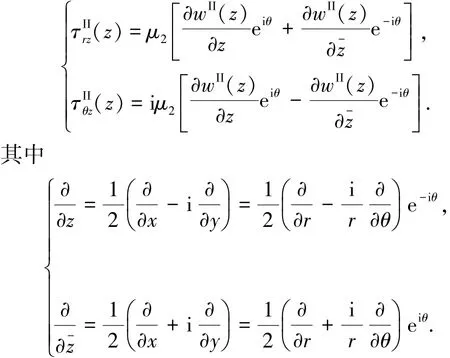
式中∂／∂z、∂／∂－z 分别为复变量z和共轭复变量－z的形式导数.这些应力都是由点源荷载2δ（z－i y0）激励产生，当y0＜R时，它们依赖于延拓的圆柱Medium II中剪切波的波数k2，当y0≤h且y0≥R时，它们依赖于延拓的半空间Medium I中剪切波的波数k1.同时，延拓的半空间和圆柱中的应力场分别是剪切模量μ1和μ2的一次函数.由此，定义量纲一的应力分量τ以及定义剪切模量比和分别为

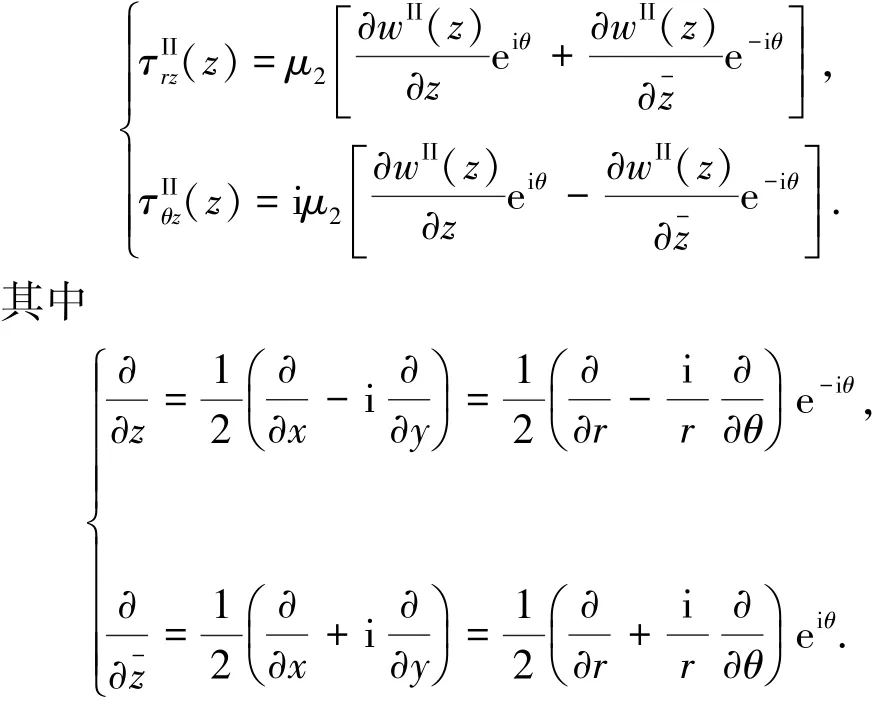
4.2 算例分析

计算延拓的半空间中的点源荷载在延拓圆柱边沿BC柱面上量纲一的径向应力分量和周向应力分量

图3 延拓圆柱边沿的动应力（h＝2R，y0＝1.5 R）

5 结 论

1）点源荷载对界面半圆柱的散射，明显地分为投射侧和影蔽侧.径向应力的投射侧和影蔽侧有明显的界限，并且在圆心与点源作用点连线上取得投射侧和影蔽侧的最大值，随着半圆柱剪切模量的增大，径向应力的最大值在投射侧几乎是影蔽侧的数倍.

2）周向应力同样在投射侧取得最大值，但并不是在正对点源荷载的方法，而是有一个偏角.

3）总体而言，随着半圆柱的剪切弹性模量的增大，径向应力也将增大，而周向应力将减小；随着半圆柱的剪切弹性模量的减小，径向应力也将减小，而周向应力将增大.

［1］MOW C C，PAO Y H.Diffraction of elastic waves and dynamic stress concentrations［M］.New York：Crane and Russak，1973.

［2］LIU Diankui，GAI Bingzheng，TAO Guiyuan.Applications of the method of complex functions to dynamic stress concentrations［J］.Wave Motion，1982，4（3）：293－304.

［3］刘殿魁，刘宏伟.SH波散射与界面圆孔附近的动应力集中［J］.力学学报，1998，30（5）：597－604.

［4］刘殿魁，史守峡.界面上圆形衬砌结构对平面SH波散射［J］.力学学报，2002，34（5）：796－803.

［5］刘殿魁，田家勇.SH波对界面圆柱形弹性夹杂散射及动应力集中［J］.爆炸与冲击，1999，19（2）：115－123.［6］田家勇，刘殿魁，刘春旭.界面固定圆形刚柱对SH波散射的远场解［J］.哈尔滨工程大学学报，1999，20（4）：90－97.

［7］齐辉，刘殿魁，史守峡.含有半圆环形衬砌的弹性半空间受线源荷载作用的位移场［J］.哈尔滨工程大学学报，2001，22（2）：81－85.

［8］齐辉，王艳，刘殿魁.半无限空间界面附近SH波对圆形衬砌的散射［J］.地震工程与工程振动，2003，23（3）：41－46.

［9］赵嘉喜，齐辉，苏胜伟.SH波对界面含有半圆形脱胶的圆柱形弹性夹杂的散射的近似分析［J］.应用数学和力学，2008，29（6）：705－712.

［10］邱发强，王慧文，王雪.SH波入射时非等腰三角形结构与基础相互作用［J］.哈尔滨工业大学学报，2010，42（4）：634－638.

［11］杨在林，许华南，陈志刚.等腰三角形凸起与半圆形凹陷地形对SH波的散射［J］.哈尔滨工业大学学报，2011，S1：6－11.

［12］折勇，齐辉，杨在林.SH波对直角平面区域内圆形孔洞的散射与地震动［J］.应用力学学报，2008，25（3）：392－398.

［13］QI Hui，SHI Yong，LIU Diankui.Interaction of a circular cavity and a beeline crack in right⁃angle plane impacted by SH⁃wave［J］.Journal of Harbin Institute of Technology，2009，16（4）：548－553.

［14］齐辉，折勇，李宏亮，等.SH波入射时垂直半空间中双相介质界面附近圆孔的动力分析［J］.爆炸与冲击，2009，29（1）：73－79.

［15］QI Hui，YANG Jie，SHI Yong.Scattering of SH⁃wave by cylindrical inclusion near interface in bi⁃material half space［J］.Journal of Mechanics，2011，27（1）：37－45.

［16］QI H，YANG J，SHI Y，et al.Dynamic analysis for circular inclusion near interfacial crack impacted by SH wave in half space［J］.Journal of Mechanics，2012，28（1）：143－151.

［17］QI Hui，YANG Jie.Dynamic analysis for circular inclusions ofarbitrary positions near interfacial crack impacted by SH⁃wave in half⁃space［J］.European Journal of Mechanics⁃A／Solids，2012，36：18－24.

［18］赵春香，齐辉，陈冬妮，等.线源荷载对半圆形凸起圆形夹杂附近浅埋圆孔的动力作用［J］.地震工程与工程振动，2013，33（3）：59－63.

［19］齐辉，赵春香，黄敏.出平面线源荷载作用下半空间内浅埋圆孔对半圆形凸起的圆柱形弹性夹杂的动力影响［J］.振动与冲击，2013，32（17）：109－112.

（编辑 张 红）

Anti⁃plane scattering of interfacial point source load and semi⁃circular cylinder in an elastic quarter space

GAO Chun1，2，QI Hui1，PAN Xiangnan1，CAI Liming1，ZHAO Yuanbo1
（1.College of Aerospace and Civil Engineering，Harbin Engineering University，150001 Harbin，China；2.Dept of Civil Engineering，Harbin University，150086 Harbin，China）

To obtain anti⁃plane elastodynamic analytic solution of a semi⁃circular cylinder，subject to anti⁃plane point source loading in a vertical bound of an elastic quarter space，image method and wave function expansion method are employed to study steady state scattering of the semi⁃circular cylinder and interaction of bounds，then displacement and stress are determined in this quarter space.More specifically，firstly，the quarter space is extended as a half space，and the semi⁃circular cylinder is also extended as a circular cylinder.Then，displacement wave is constructed as series form of wave function and circular cylindrical bound is expanded as Fourier series to determine coefficients of wave function finally.Dynamic stress distributed around circular cylinder is calculated to show that scattering of the semi⁃circular cylinder is apparently to distinguish front and back，and relative low frequency of loading usually causes more dynamic stress around the semi⁃circular cylinder，and material parameters also have two widely divergent influences on the radial and circumferential dynamic stress distribution.This steady state solution is presented to enrich SH wave scattering theory and to formulate Green function method for SH wave scattering of bi⁃material interfacial circular cylinder with theoretical analysis.Numerical calculating examples demonstrate the related engineering problem for underground engineers，earthquake engineers，geotechnical engineers and civil engineers as well.

SH wave scattering；point source；interfacial circular cylinder；quarter space；dynamic stress distribution

O343.1；O326

A

0367－6234（2015）10－0094－06

10.11918／j.issn.0367⁃6234.2015.10.018

2014－01－02.

国家自然科学基金（51379048）.

高 春，（1975—），女，副教授，博士研究生；齐 辉，（1963—），男，教授，博士生导师.

潘向南，panxiangnan＠hrbeu.edu.cn.