论三角函数的无理性

北京师范大学 吕孙忠 (邮编：100875)

北京师范大学珠海分校应用数学学院 高文华 (邮编：519085)

论三角函数的无理性

北京师范大学 吕孙忠 (邮编：100875)

北京师范大学珠海分校应用数学学院 高文华 (邮编：519085)

文[1]中提出了一个关于三角函数的问题：对怎样的整数n，sinn°和cosn°当中至少有一个是有理数？文[2]对这个问题做了进一步的探究.但这两篇文章对n的讨论，仅仅局限于整数集上，笔者基于文[2]的研究基础上，扩大n的数域，再给出了若干结论.

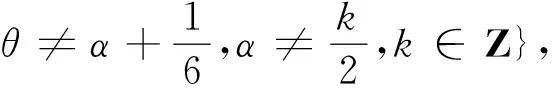
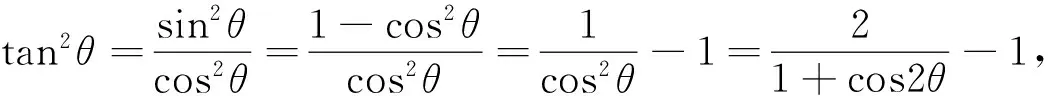
文[2]中讨论了当n为奇数时，若cosnθ为无理数，则cosθ为无理数.

推论1 若cosnθ为无理数，则cosθ为无理数，其中n∈Z.

证明 将cosnθ展开，得cosnθ=a0cosnθ+a1cosn-2θ+……+ak，其中a0,a1,……ak均为整数，若cosnθ为无理数，则cosθ必为无理数.

推论2 若tanθ为有理数，则tan(nθ)为有理数，其中n∈Z.

证明 同样用数学归纳法可证，此处略.

例 ( 2014 年北约)证明tan3°是无理数．

我们知道kπ=k×360°，它在弧度制中是无理数，而在度的单位中却是一个整数.如果将单位转为度，那么在正弦，余弦和正切中，对∀θ∈(0,90)且θ∈Q，只有sin30°，cos60°和tan45°为有理数，在度的单位中做一点讨论.

推论6 如果一个三角形的三边都是有理数，若内角的度数为有理数，则该内角的大小只能是60°，90°，120°.

证明 根据余弦定理和引理1，即证明.

推论7 如果一个三角形的三边和三个内角的度数均为有理数，则该三角形一定是等边三角形.

证明 根据推论5，可得该三角形三个内角为60°，90°，120°之一，推理可得内角只能为60°，所以该三角形为等边三角形.

推论7的条件也可放宽至两个内角为有理数，因为若三角形的两个内角为有理数，那么第三个内角也必为有理数.

思考 当θ=nrad，n为有理数且n≠0时，能否用初等方法证明sinθ和cosθ为无理数.(该问题可以用超越数理论解决)

1 卢莉英．由计算sin18°而联想的[J].数学通报，2011(3):60-61,63

2 郝四柱．整数度数的正余弦何时才能是有理数[J].数学通报，2014(1):53-54

3 王萼芳，石生明.高等代数第三版[M].北京：高等教育出版社，2003

4 喻沛如.再谈三角函数的无理性[J].江西教育学院学刊，1982(1):51-52

5 闵嗣鹤，严士健.初等数论第三版[M].北京：高等教育出版社，2005

2015-03-05)