对一道高考数学压轴题的研究

湖北省武汉市黄陂六中 梅 磊 (邮编：430300)

对一道高考数学压轴题的研究

湖北省武汉市黄陂六中 梅 磊 (邮编：430300)

2014年高考数学湖北卷文科压轴题(理科次压轴题)如下：

在平面直角坐标系xOy中，点M到点F(1,0)的距离比它到y轴的距离多1．记点M的轨迹为C.

(Ⅰ)求轨迹C的方程；

(Ⅱ)设斜率为k的直线l过定点P(-2,1). 求直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.

本题立足课本上的通性通法，考查求轨迹方程的基本方法、直线与抛物线的位置关系，考查函数与方程的思想、分类与整合的思想，考查推理论证能力和运算求解能力.该题运算量适中，难度适宜，贴近课本，两问衔接自然，充分体现了解析几何的本质，使得考生的理性思维和学科能力得到充分的考查.

1 解法分析

第(Ⅰ)问求轨迹C的方程，考查曲线与方程的对应关系，直接由题意列出动点M的坐标满足的关系式|MF|=|x|+1，再化简即可，此问是考生所熟知的类型，有利于稳定考生的情绪，增强解题的信心.

第(Ⅱ)问判断直线l与轨迹C的交点的个数，可以用解析法来解决，即要讨论直线l方程与轨迹C的方程组成的方程组的解的情况，由方程组的解的情况判断直线l与轨迹C的交点的个数，体现了转化与化归的思想.注意到轨迹C的方程可以分为两个部分(可分别记为C1和C2)，可以分别讨论直线l的方程与C1的方程组成的方程组的解的情况和直线l方程与C2的方程组成的方程组的解的情况.在讨论直线l方程与C1的方程组成的方程组的解的情况时，要分k=0和k≠0两种情况讨论，且在k≠0这种情形中又要分△=0，△>0和△<0三种情况讨论，反复体现了分类与整合的思想，此问也是考生所熟知的类型，有利于考生征服压轴题，体验成功的喜悦.

具体解答如下(与参考答案略有不同)：

(Ⅰ)设点M(x,y)，依题意当x≥0时，点M(x,y)到点F(1,0)的距离与它到直线x=-1相等，由抛物线定义知，此时点M的轨迹C的方程为C1:y2=4x;

当x<0时，点M(x,y)到点F(1,0)的距离与它到直线x=1相等，显然，此时点M的轨迹C的方程为C2:y=0(x<0).

(Ⅱ)依题意，可设直线l的方程为y-1=k(x+2).

(1)先考虑直线l和C2的公共点的个数.

当k=0时，直线l与x轴平行，此时直线l与C2无公共点；

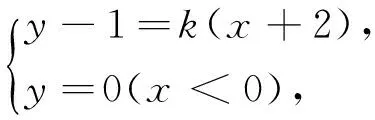
(2)再考虑直线l和C1的公共点的个数.

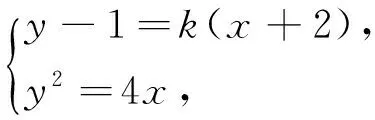
当k=0时，易知，直线l与C1恰有一个公共点.

当k≠0时，方程ky2-4y+4(2k+1)=0的判别式为△=-16(2k2+k-1).

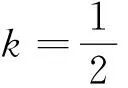
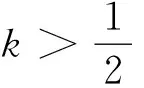
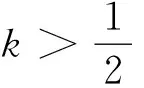
2 题源探究

看到此题，我们不难联想到下面三道题.

题源1 (1990年希望杯高二第一试第13题)若平面内的动点P到定点F(1,0)的距离比P点到y轴的距离多1．则动点P的轨迹方程是______.

题源2 (2011年湖南高考文科数学第21题)已知平面内的动点P到定点F(1,0)的距离与点P到y轴的距离的差等于1．

(Ⅰ)求动点P的轨迹C的方程；

题源3 (人教A版选修1-1课本第62页例5，选修2-1课本第71页例6)已知抛物线的方程为y2=4x，直线l过定点P(-2,1)，斜率为k.当k为何值时，直线l与抛物线：只有一个公共点；有两个公共点；没有公共点.

显然，试题由上述三道题整合加工而成，其中试题的第(Ⅰ)问与题源1和题源2的第(Ⅰ)问如出一辙，都是求轨迹C的方程，求解方法也一样；试题的第(Ⅱ)问与题源2极为相似，直线l过定点P(-2,1)坐标完全一样，试题判断直线l与C1的交点个数与题源2完全相同；试题判断直线l与C2的交点个数与题源3完全类似.

3 导向解读

本题满分14分，其中第(Ⅰ)问5分，第(Ⅱ)问9分.考生只要了解求曲线的方程的基本方法，解答第(Ⅰ)问是很容易.如果考生掌握判断直线与抛物线公共点个数的基本方法，解答第(Ⅱ)问也是不难的.故对于大多数考生而言，可以拿到一半左右的分数.

然而，本题的实测结果却不尽人意，文科考生的平均分仅为2.18，理科考生的平均分也仅3.71分，远远低于预期.

为什么会出现这样的结果呢？

长期以来，说到高考数学压轴题，在很多师生眼中，那是尖子生的天下.从压轴题的功能看，应该具有必要的难度和较强的区分度，有利于高校选拔优秀人才.为此，命题组担心的是压不压得住的问题，而高中师生考虑的则是做不做的问题，命题与应试之间的矛盾凸显无疑.在认同命题者水平的前提下，值得引起我们注意和反思的一个误区，就是部分高中数学教师指导学生复习备考的“异化”现象：即明确告诉学生不要在压轴题上浪费过多的时间，甚至干脆让学生放弃压轴题.在这种应试意识的影响下，教师自己也疏于对压轴题的研究，不愿意或舍不得花时间去领悟压轴题的味道，从而也就难以指导学生去研究压轴题，挑战压轴题，征服压轴题.这种消极的影响造成考生对压轴题的心理畏惧是可想而知的.每年总有部分考生因为时间关系无暇顾及压轴题，这是正常的，但仍有不少考生在时间允许的情况下完全放弃压轴题，甚至考后连压轴题是什么样的题都不知道，这就不正常了.

2014年高考数学湖北卷文科压轴题(理科次压轴题)发出的信号是强烈的：不要完全放弃压轴题，而要勇敢挑战压轴题，压轴题一般都会设置层次分明的台阶，入口宽，上手易，只是深入难，解到底难，但即使难，解题所用的方法也是通性通法和常规常法.

其实，对于所有认真复习备考的同学来说，都有能力与实力在高考数学压轴题上拿到一半左右的分数，要获取这一半左右的分数，不需要大量针对性训练，也不需要复杂艰深的思考，只需要你有正确的心态！信心很重要，细心不可少.

对于教师而言，更要提高自身对压轴题研究的意识和水平，帮助考生掌握正确解答压轴题的策略，走出解答压轴题的误区.

1 梅磊.求解一道2014年高考数学压轴题的心路历程[J].中学数学教学，2014(6)

2015-03-03)