三个变量 四种层次

浙江省嘉兴市秀州中学 屠新跃 (邮编：314033)

三个变量 四种层次

浙江省嘉兴市秀州中学 屠新跃 (邮编：314033)

问题 设集合M={(a,b)|a≤-1，且b≤m}，其中m∈R．若对任意的(a,b)∈M，均有a·2b-b-3a≥0，求实数m的最大值．

1 主元思想

就是把问题理解为一个变量的函数值在其定义域上恒大于或等于零，关键是求出这个函数的最小值，一般可以先研究这个函数的单调性．那么，以哪个变量作为主变量，应当是首先要确定的问题．

1.1 以a为主变量

设函数f(a)=(2b-3)·a-b，则f(a)的图象就是直线或其一部分．而要使a≤-1时，恒有f(a)≥0，则a的系数只能满足2b-3≤0．否则，若2b-3>0，则f(a)是(-, -1]上的增函数，则有一次函数f(a)→ -，不合题意，舍去．

因此2b-3≤0，则f(a)最小值是f(-1)=-2b+3-b≥0，即2b+b≤3．又b≤m，考虑函数y(b)=2b+b是在R上递增，则y(b)≤y(m)=2m+m，且恰有y(1)=3，则m≤1.

所以，m的最大值就是1．

1.2 以b为主变量

设函数g(b)=a·2b-b-3a，由于a·2b(a≤-1)和-b都是R上的减函数，所以g(b)在(-,m]上递减，则g(b)的最小值是g(m)=a·2m-m-3a≥0，a(2m-3)≥m，若2m-3≥0，右边=m≥log23>0，而a≤-1，左边≤0，则a(2m-3)≥m不可能成立，则2m-3<0，那么有-(2m-3)≥m，m+2m≤3，同理有m≤1，则m的最大值是1．

2 分离变量

问题的本质就是求变量b的最大值，这样三个变量就变成了两个变量，那就可以尝试将这两个变量a,b分离．也就是通过变形，能使得不等式的两边各含有一个变量，再求某一边的最值来解决问题．

由已知得(2b-3)·a≥b，再对2b-3的符号进行讨论，达到变量a,b分离．

当2b-3=0，右边=b=log23>左边=0，舍去；

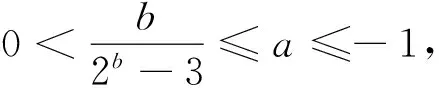
题中的不等式a·2b-b-3a≥0，可以转化为两个函数取值的大小关系问题，借助这两个函数的图形，通过观察比较，就可以直观地在画出的图形中，寻找它们的高、低(大、小)关系．

这里，应先转化为相对简单的两个函数形式，以便于在同一个坐标系下分别画出它们的图象．

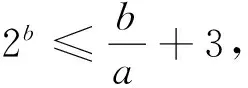
4 必要条件

对题设中给定范围的变量a，取一些特殊值来代入，可求得另一个变量b的范围A，它必定是要求的变量b的结论B的必要条件，也就是必须有B⊆A．这样，就可以有力地缩小b的取值范围，使问题得到优化，然后可以对结论作大胆的猜想，在这个基础上，再去证明猜想就是问题的充分条件．

根据题意，“a=-1，b=m”，是“a·2b-b-3a≥0”恒成立的一个必要条件，代入得

-2m-m+3≥0，2m+m≤3，同理有m≤1，就可以猜想m的最大值是1；而当b=1代入a·2b-b-3a≥0，得2a-1-3a≥0，则a≤-1，这就证明了它的充分性．

所以，m的最大值是1．尽管这样的解法有其一定的偶然性，但不失为一种很好的思维方式，至少可以使未知变量的范围得到有效的控制．

2015-01-05)