课堂,何必绑定教材？——“三角函数的诱导公式”的教学随笔

江苏省南通市小海中学 蒋 昊 (邮编：226015)

课堂,何必绑定教材？
——“三角函数的诱导公式”的教学随笔

江苏省南通市小海中学 蒋 昊 (邮编：226015)

1 教材中采用的建构方式

年初,笔者上了一堂高中数学课,课题是：《三角函数的诱导公式(1)》，其四组诱导公式的呈现方式如下：

①由三角函数定义可知，终边相同角的同一三角函数值相等.

sin(2kπ+α)=sinα(k∈Z)

cos(2kπ+α)=cosα(k∈Z)

tan(2kπ+α)=tanα(k∈Z)

(公式一)

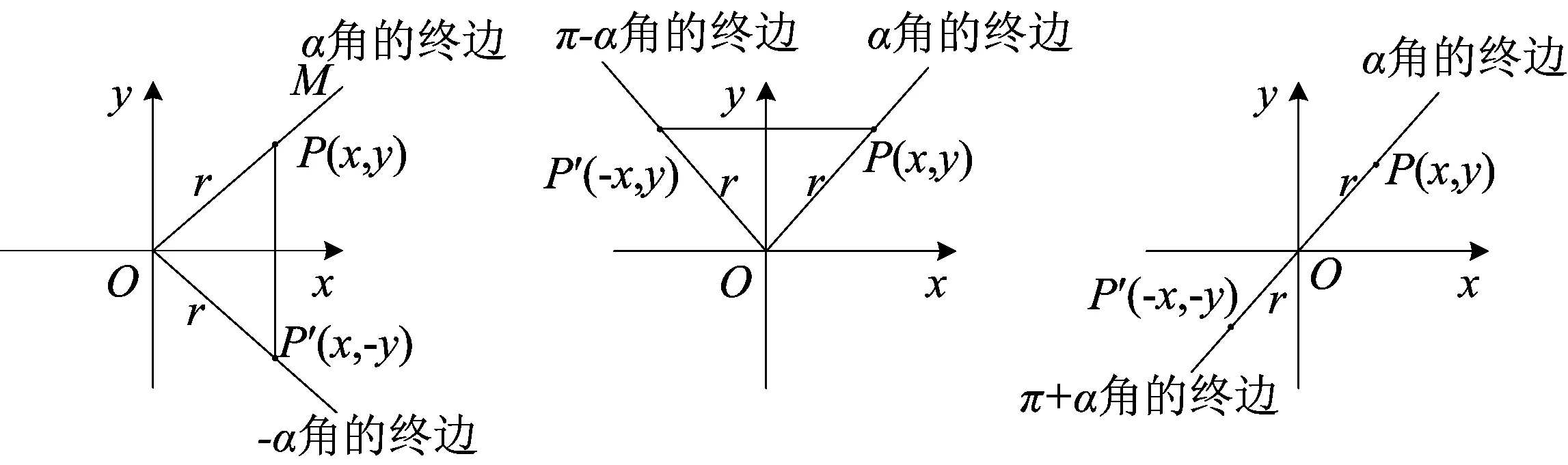
②α、β角的终边关于x轴对称，如图(1)：

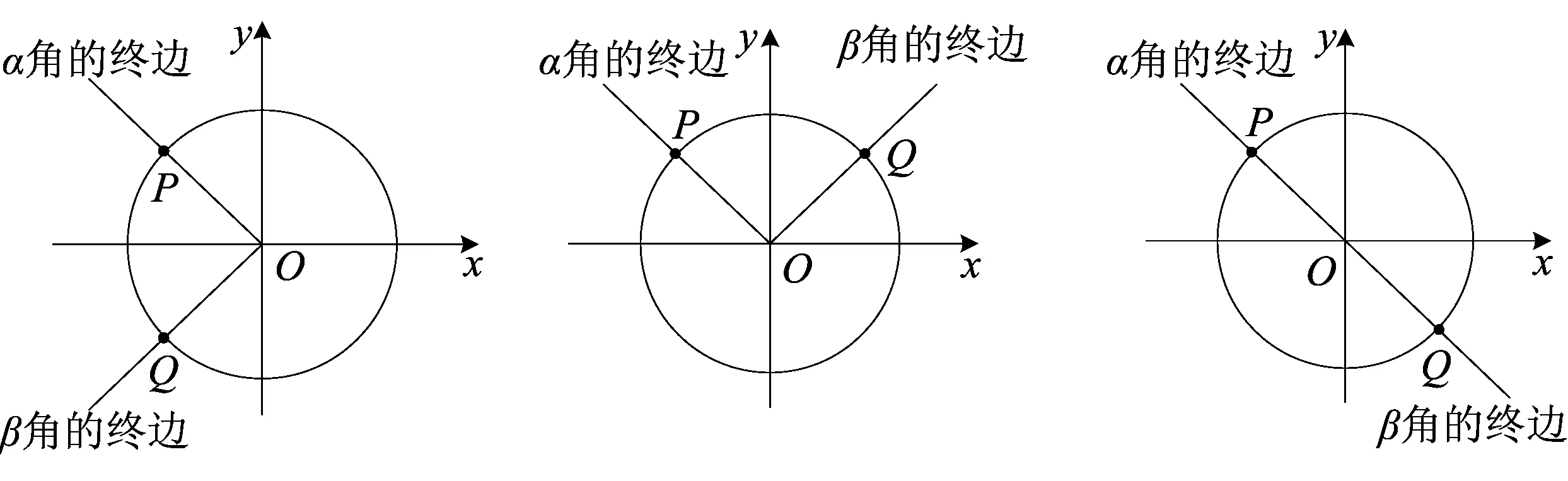
(1) (2) (3)

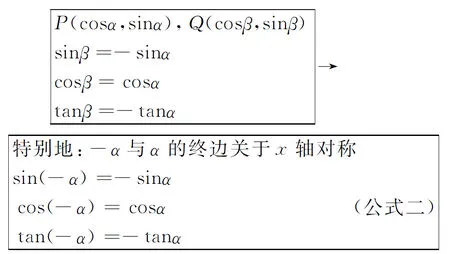
③α、β角的终边关于y轴对称，如图(2)：

④α、β角的终边关于原点O对称，如图(3)：

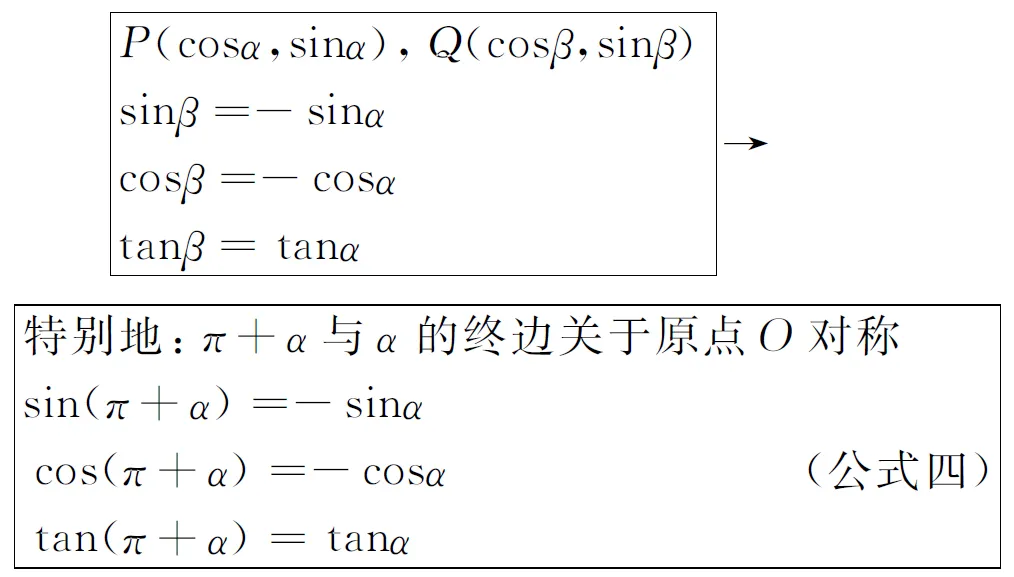
其中，对于公式(2)、(3)，执教者试图由学生通过公式(2)的推导过程而类比推得，事实上处理得并不成功.这节课的知识生成全盘采用了苏教版教材《普通高中课程标准实验教科书·数学Ⅳ》中 “§1.2.3三角函数的诱导公式”的呈现方式，课堂教学过程中学生反应一般.课后笔者一直在思考，对于本节课脑海中始终萦绕着一些疑问：讲解本课时单位圆非用不可吗？教材中知识的建构方式是不是唯一的？其建构方式是否适合所有的学生？适合我自己班的学生吗？课堂，是否必须绑定教材？

2 笔者教学时的建构方式

基于对以上问题的思考，笔者在另一个班执教《三角函数的诱导公式(1)》这节课时，并未采用教材中的呈现方式，转而直接从三角函数的定义出发引导学生发现四组诱导公式：

情景一 利用ppt动画分别演示三角函数定义；演示点P在终边上移动以及演示将α的终边旋转β和旋转2周，并提出以下问题：

问题1 在平面直角坐标系中，如何定义任意角α的正弦、余弦和正切的呢？

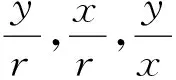
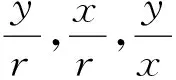
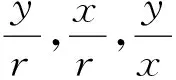
问题5OM除了是α的终边，还可以是哪些角的终边？

问题6 角α的终边和角2kπ+α的终边是重合的，那么它们的三角函数值有怎样的关系？

情景二 将α的终边OM旋转到关于x轴对称位置ON.如图(4)

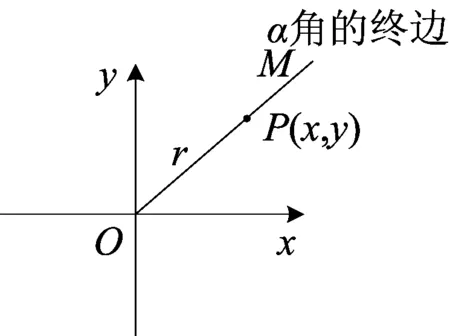
问题6 将OM旋转到ON,使得ON和OM关于x轴对称，那么ON可以是哪个角的终边?

问题7α和-α的终边关于x轴对称，那么它们的三角函数有什么关系呢?

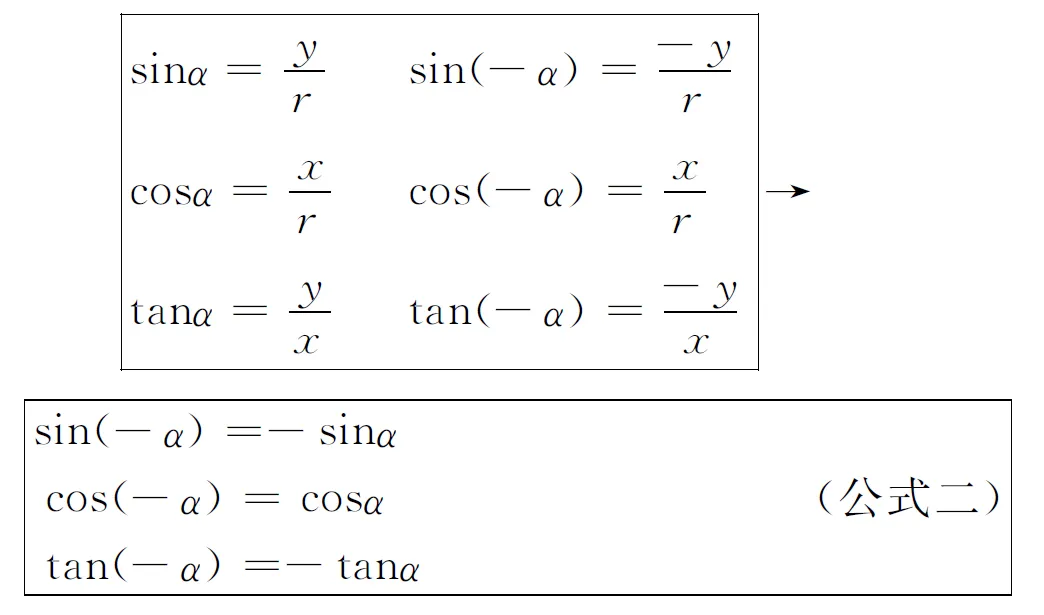
情景三 以小组合作学习的方式探究诱导公式(三)和(四).如图(5)和(6)

(4) (5) (6)

问题8 如果让你继续探究，你将探究什么呢？

分两组探究：甲组探究关于y轴对称，乙组探究关于原点对称．甲乙两组分别汇报探究结果，得到诱导公式(三)(四).

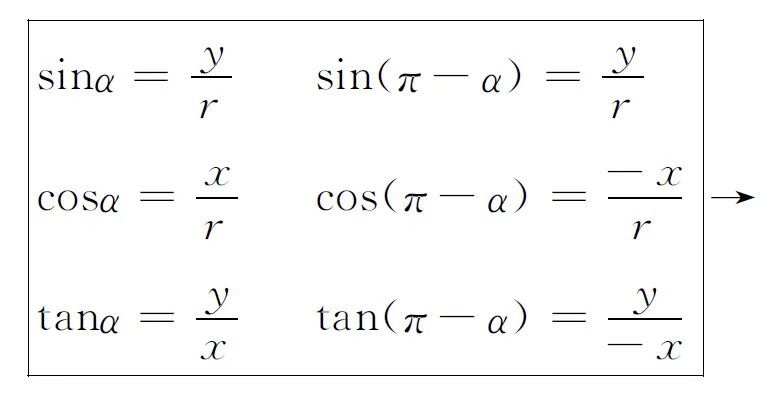
3 两种建构方式的比较

从要求学生具有的知识储备的角度来看，教材中提供的建构方式是建立在“任意角三角函数的定义”的基础上，以单位圆为工具，结合“三角函数线”，“同角的三角函数关系式”等知识点，从而实现三角函数四组诱导公式的生成.而笔者教学时紧扣了问题本质，即以“三角函数的定义”为核心，围绕四种终边位置关系展开，建构过程中摈弃单位圆，不把问题特殊化，基于一般性的条件，始终仅依靠“三角函数的定义”来探求三角函数的四组诱导公式.

从学生的接受程度来看，教材中的建构方式对学生综合运用所学知识解决问题的能力要求较高.如果学生基础薄弱，或对之前所讲的部分知识点存有漏洞，那么在学习本课时会产生疑惑，对诱导公式的生成过程不明其理.在教学时，一下子把 “单位圆”、sinα、sinβ、cosα、cosβ、tanα、tanβ以及α、2kπ+α、π-α、π+α等若干数学量统统呈现出来，学生是很难理出头绪的.即便在老师讲授公式二的基础上，试图让学生快速理解掌握建构方式，并举一反三也是不易的，这也就是为什么在观摩课上教师让学生自主探究公式(三)、(四)而卡壳的原因.反观笔者的课堂教学，教师在示范性地引导学生推导出“终边位置相同”的“角α”与“角2kπ+α”之间的三角函数关系式即公式一，以及“终边关于x轴对称”的“角α”与“角-α”之间的三角函数关系式即公式二后，学生的自主探究目标也就此明确下来即探究“终边关于y轴对称”的“角α”与“角π-α”和“终边关于原点对称”的“角α”与“角π+α”.由于推导过程始终依托“三角函数的定义”，因而老师推导完公式二后学生对于探究方法一目了然.在教学过程中，也的确反映出学生对于公式(三)、(四)的推导极易掌握.

4 教学感想

通过对《三角函数诱导公式(1)》这节课建构方式的思考，笔者深刻认识到课堂教学，绝不应该绑定教材！

教师是知识的传播者，而不是教材的解说员.如果一个教师始终把自己定位成一个“教书匠”，那么他的教育教学工作必然是要被淘汰的，同时他也看轻了教师这份职业.我们不应该单纯的停留在把教材上的内容告知给学生，我们传授的是“知识”不是“教材”.对于教材我们要有准确的定位，它仅仅是我们开展教学工作的工具，不是我们教学的唯一依据.我们应该研究教材，在教材的基础上有自己的思考，有自己的发展和延伸，甚至于有时要敢于合理地怀疑教材，抛开教材来传授知识.这也正是教师之所以能成为教师的原因.

新课程理念积极倡导把学生看作学习和发展的主体.作为教师不能把“学生是学习的主体”停留在口头上，不能片面地将“主体”等价于让学生自主探究，自主发现.学生是我们课堂教学的直接受众，真正的“主体”应该体现在教师是否能时刻站在学生的角度上去考虑我们的教学，建构我们的课堂.诚然，教材的编者是在中学数学教材教法方面卓有研究的专家，但这并不能成为我们惰性思考的借口，也不能成为我们照本宣科的理由.教材中的建构方式必然是经过考虑的，但不代表适合所有的学生，不代表这是唯一的呈现方式，更不代表这种建构方式一定为我们的学生所接受.正如陶行知先生所言“培养教育人和种花木一样，首先要认识花木的特点，区别不同情况给以施肥、浇水和培养教育”.这才叫“因材施教”！最了解班级学生的是教师，而学生需要的是最适合自己的课堂，这就要求教师不能被教材绑着走，要努力钻研提高业务水平，要从班级学生的实际出发，建构课堂，生成知识.从而打造一个真正传播知识，因材施教的课堂.

1 教育部.普通高中数学课程标准(实验)[S].北京:人民教育出版社,2003

2 单墫.普通高中课程标准实验教科书·数学Ⅳ[M].南京:江苏教育出版社,2007

3 罗小军.优化课堂资源 建构有效课堂[J].甘肃教育,2009(2)

2015-04-13)