扫描轨迹下的分段迭代补偿策略

魏 凯 范文超 陈兴林 张广莹

(哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001)

扫描轨迹下的分段迭代补偿策略

魏 凯 范文超 陈兴林 张广莹

(哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001)

为提高光刻机掩模台系统的步进扫描品质，进而提高硅片成品质量，提出一种基于S曲线的轨迹规划。对迭代学习控制进行了研究，并针对普通全局迭代算法可能造成系统在特定环节恶化的局限性，采用分段迭代补偿策略，对迭代学习控制器进行分段优化。仿真表明，分段迭代学习控制满足系统的实际需求，可以应用在掩模台系统的调试中。

光刻机 掩模台 步进扫描 S曲线 分段迭代学习控制

0 引言

在对硅片的处理过程中，光刻机掩模台系统主要采用步进扫描的方式进行运动。其运动的品质与成品的质量息息相关，而步进的速度又决定了系统的产率。除了系统本身的高性能之外，轨迹规划也起到不容忽视的作用。合理的轨迹规划不仅能减小系统运动过程中的机械冲击，还能使系统的运动轨迹更加平滑[1-2]。而对于迭代学习控制而言，单纯的在光刻机的运动轨迹中使用迭代学习确实能起到一定的作用，但有时却事与愿违。文献[3]中直接采用了全时段的非因果迭代学习控制率，出现了曝光阶段性能无法提高甚至部分恶化的现象。这是由于其忽略了扫描光刻系统的工作特点，全时段的迭代有时会由于动态过程而牺牲系统稳态过程性能[4-6]。本文从光刻机掩模台工作轨迹的特点入手，将原有的迭代学习控制进行分段，期望获得更好的控制效果。

本课题来源于国家科技部“十二五”重大科技发展专项“极大规模集成电路制造装备与成套工艺专项”的子课题“扫描步进式光刻机双工件台控制系统研制”。

1 扫描光刻系统轨迹规划

在步进扫描的过程中，硅片台在一个曝光域的曝光完成后，要步进到下一个曝光区域，重复扫描曝光的过程。300 mm的标准晶圆上通常分布着80～100块曝光小块(Die)，曝光小块的大小与曝光狭缝和扫描的长度有关，而曝光狭缝的大小又取决于投影物镜的视场。扫描的过程伴随着动态曝光的过程，从一个曝光小块步进到另一个曝光小块的过程称为Die-to-Die的运动过程[7]。

Die-to-Die的过程包含y轴方向的扫描运动和x轴方向的步进运动。对于掩模台的宏动部分而言，由于不存在x轴方向的自由度，因此只需讨论y轴方向的扫描运动。在台体一个轨迹周期的往复运动过程中，为减小硅片台在加减速过程中对系统框架的冲击，实际工程中普遍采用S曲线进行轨迹规划。S曲线通过使轨迹加速度曲线平滑连续来避免机械冲击，进而减小对台体的损害。普遍采用的S曲线轨迹设计方法是：设计出一个准则J，给定边界条件，在满足这些边界的前提下，找到能够使优化准则J最小的解来规划轨迹。常用的S曲线设计准则有时间最优、力最小、能量最小、冲击最小以及它们的复合准则等。表1列出了S曲线相应的边界条件和轨迹表达型式，以便对比。

表1 S曲线主要设计准则

单纯的时间最优规则只考虑时间的最优解，而不考虑曲线连续性、冲击、能量等因素，通常不直接作为实际轨迹使用，而是考虑与其他规则配合。能量最小的方法在某种程度上可以等效于驱动器输出受限的时间最优法，但是光刻系统并不对能耗做任何要求，所以也不适用本系统。复合法是一种考虑非常全面的方法，它利用了曲线线性的特点，可以考虑到几乎所有的约束准则；并根据实际情况调整权重系数qi的值，使轨迹能够满足某些系统的苛刻要求。对于扫描光刻系统，由于系统对测量精度要求极高，也就必须避免一切不必要的机械冲击，且系统追求效率，因此，通常结合使用冲击最小和时间最优的准则对S曲线进行设计。一个典型的5阶S曲线如图1所示。

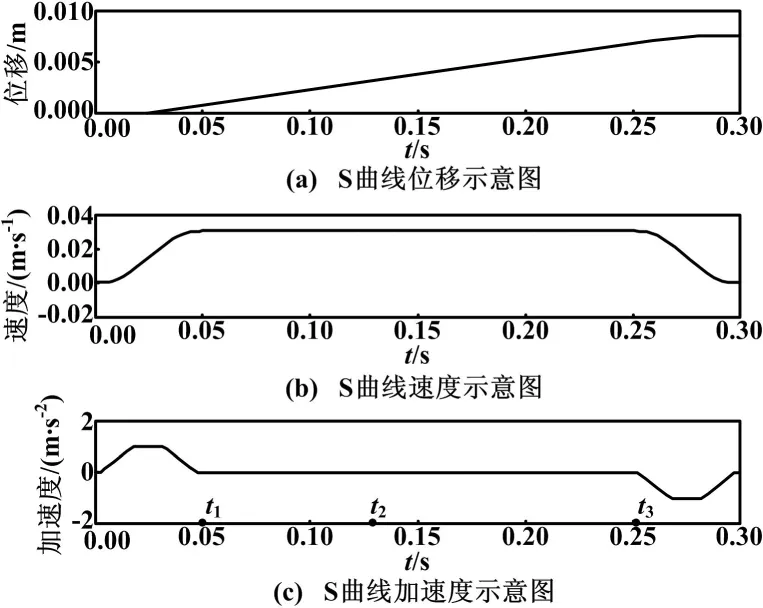
图1 一个周期行程的S曲线示意图

除了对速度和加速度进行限制外，还需对系统的加速度进行限制，使整个跟踪轨迹较为平滑。

参考轨迹包含了以下几个过程：①从零时刻经过加速过程到达t1时刻；②t1～t2时间段为加速结束后的动态调整过程，称为调节时间；③t2～t3时间段为匀速扫描曝光阶段，此时对硅片进行动态曝光；④t3时刻后，系统将进入减速阶段，此时一个曝光小片的曝光结束。

从t3时刻开始，台体在减速的同时，沿x轴方向进行步进运动，直到运动到下一个小片的起始位置，然后沿着y轴相反的方向进行扫描曝光[7]。

根据上述条件得到一个5阶S曲线的表达式如下。

(1)

(2)

式中：vs为扫描速度；ls为加速过程的位移；ρ为一个正常数参数。

将实际数据代入计算，一个位移为30 mm的5阶S曲线的整个行程的示意图如图2所示。从图2可以看出，轨迹的前后两部分存在对称关系。

图2 5阶S曲线完整周期

2 分段迭代学习控制

2.1 分段迭代学习控制器设计

为了更好地利用分段迭代学习对控制量的预测和稳定效果，对上述轨迹进行分析。如图2所示，在扫描段的t1、t3、t5、t7是加速度变化最为剧烈的几个关键时刻，在反馈作用下，也是跟踪误差变化最大的时刻。若系统已经对前一个迭代周期的完整时间段内的误差进行学习，则在上述几个时刻周围都会引起强烈的学习控制作用。然而，这些控制作用是否都是积极的值得进一步探讨。可以预见，在反馈和迭代学习的共同控制作用下，t2～t3段和t6～t7段作为光刻系统的匀速扫描过程相对稳定，会获得较好的跟踪性能，因为此时无论是推理波动还是系统模型都相对稳定，具有很强的规律性。而在t0～t2段和t4～t6段，系统处于剧烈的动态调节过程，系统模型可能受到多种扰动，跟踪性能会大打折扣。因此，在t1和t5时刻，系统由动态特性变化到静态特性，学习控制可以有效减小调节时间；而t3和t7时刻的学习作用由于与t1和t5时刻是对称的，系统由静态特性变化到动态特性，此时的学习控制为了改善减速阶段的性能，很可能牺牲周围区域的跟踪特性。显然，前者对系统的扫描性能的影响是所期望的，而后者则不然[8-11]。因此，引入分段学习控制的思想有充分的必要性。根据上述分析，可将扫描光刻系统的学习控制作用分为六段。第Ⅰ段为t0～t2区间，第Ⅱ段为t2～t3区间，第Ⅲ段为t3～t4区间，第Ⅳ段为t4～t6区间，第Ⅴ段为t6～t7区间，第Ⅵ段为t7～1.0 s区间。则在原有学习控制律Ls的基础上，通过引入分段学习加权正定阵，进而得到分段迭代学习控制律的矩阵形式，可以表达为：

L=L1+L2+L3+L4+L5+L6=

W1LsW1+W2LsW2+W3LsW3+

W4LsW4+W5LsW5+W6LsW6

(3)

2.2 分段迭代学习收敛性证明

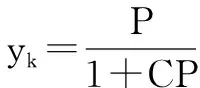
(4)

(5)

实际上，有限时间段内的迭代学习控制律是对频域内迭代学习控制律的有效截短。对于稳定的学习控制律而言，这样的处理不仅不会影响算法的收敛性，而且会改善系统在最关键的匀速扫面段的性能。

3 系统仿真

为了验证上述理论，首先将生成的S曲线导入到系统模型当中作为位置给定输入，系统的其他结构保持不变。此时按照原有的迭代学习控制率进行仿真，得到的结果如图3所示。

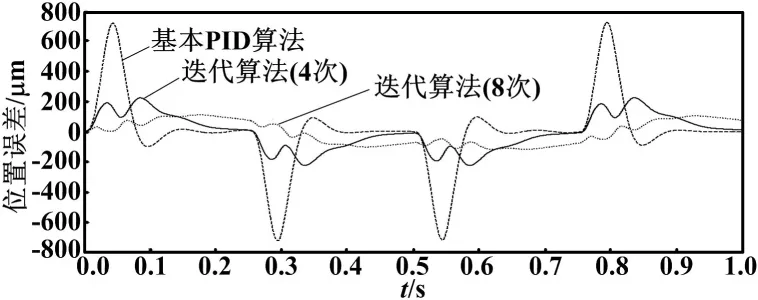
图3 全局迭代S轨迹的系统误差曲线

从图3可以看出，正如上文分析的一样，常用的反馈控制律往往在过渡过程段性能较差，迭代学习控制的优点是可以改善过渡过程段的跟踪性能。经过8次迭代学习控制之后，直线电机在加速段的动态误差得到了很好的抑制。然而，在匀速扫描阶段，系统的误差曲线却出现了明显的劣化。在速度和位置控制环PID控制器的作用下，直线电机系统经过调整时间之后,在匀速段由定位力扰动引起的误差被控制在19 μm以内。但是由于有全局迭代学习的引入，作为抑制动态加速段的跟踪误差的副作用，该匀速段的误差峰值甚至达到了108 μm。即使不对电机定位力扰动进行补偿，也不应出现如此大的跟踪误差。这种结果显然是不能接受的，毕竟对于光刻扫描系统而言，最关键的阶段就是匀速扫描阶段，这一段的系统性能应该得到最高优先级的保证。因此，基于仿真试验的结果，进行分段迭代控制的必要性毋庸置疑。

由于完整S轨迹的对称性，先对其上升阶段进行分段试验。上升段包含了之前规划的第Ⅰ段(t0～t2区间)、第Ⅱ段(t2～t3区间)以及第Ⅲ段(t3时刻之后)。由于迭代学习控制对于系统动态性能有显著提高，所以在第Ⅰ段和第Ⅲ段仍应尽量发挥迭代学习控制的作用。而对于匀速扫描阶段第Ⅱ段，则要在保证其对直线电机定位力扰动补偿作用的前提下，适当削减由区间周围的剧烈误差变化学习作用。经过对PID型迭代算法参数的反复调节，得到如图4、图5所示的仿真曲线。

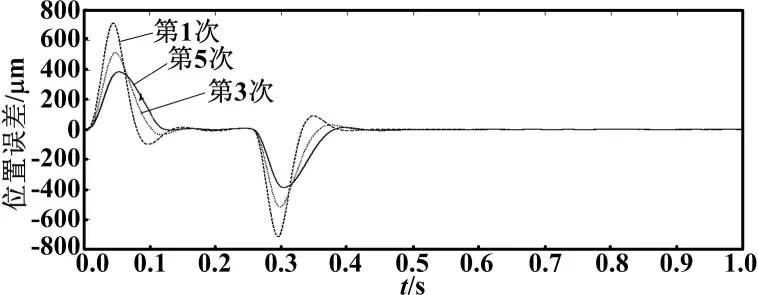
图4 S轨迹的系统误差曲线

图5 S轨迹的系统匀速段误差曲线

从图4和图5可以看出，经过对迭代学习进行分段之后，系统在匀速段的控制效果得到了明显改善，而加速段虽然不及原算法效果显著，但是仍在迭代学习控制之下有明显的收敛趋势。对曲线匀速段进行放大观察，可以看到，经过时间段0.15～0.25 s的匀速扫描区间，电机的定位力扰动依然得到了有效补偿，波动幅值从原始的19 μm减小到了8 μm以内，削减了约57.8%。

对全局迭代的方式和分段迭代的方式得到的误差二范数进行比较，结果如图6所示。

图6 沿迭代轴的误差二范数曲线

将分段方法和对应的参数对称地扩展到整个S曲线，仿真结果如图7所示。

图7 完整S曲线分段迭代曲线

可见，在S曲线全行程上，上述分段迭代学习方法确实适用，其匀速扫描阶段的细节部分和图6一致。因此，相比全局迭代算法，分段迭代学习补偿控制才真正满足系统的实际需求。

4 结束语

在实际系统中引入迭代学习控制算法时，虽然可以满足收敛性，但是往往会造成系统在特定环节的劣化。为此，针对光刻机实际扫描过程的轨迹需求，对迭代学习控制器进行分段优化，并通过仿真证明了其可行性。

[1] 吴敏镜.超精密加工的技术基础和创新[J].新技术新工艺,2006(5):7-10.

[2] 李艳秋.光刻机的演变及今后发展趋势[J].微细加工技术,2003(2):1-5.

[3] Mishra S,Tomizuka M.Projection-based iterative learning control for wafer scanner systems[J].Mechatronics,IEEE/ASME Transactions on,2009,14(3):388-393.

[4] Lee J H,Lee K S,Kim W C.Model-based iterative learning control with a quadratic criterion for time-varying linear systems[J].Automatica,2000,36(5):641-657.

[5] Butcher M,Karimi A.Linear parameter-varying iterative learning control with application to a linear motor system[J].Mechatronics, IEEE/ASME Transactions on,2010,15(3):412-420.

[6] De Roover D,Bosgra O H.Synthesis of robust multivariable iterative learning controllers with application to a wafer stage motion system[J].International Journal of Control,2000,73(10):968-979.

[7] 陈兴林,姜晓明,王岩.扫描光刻系统的分段迭代学习控制策略[J].Journal of Harbin Institute of Technology,2013,45(7):18-23.

[8] 胡玉娥,翟春艳.迭代学习控制现状与展望[J].自动化仪表，2005，26(6):1-4.

[9] 张奕,王喜顺.迭代学习的高速伺服系统位置控制策略[J].自动化仪表，2010，31(2):21-24.

[10]全权,魏子博,高俊,等.软管式自主空中加油对接阶段中的建模与控制综述[J].航空学报,2014(9)：2390-2410.

[11]尚桦,李海军,闫清,等.迭代学习控制的分析与仿真[J].自动化技术与应用，2013(8)：6-9.

Segmented Iterative Compensation Strategy under Scanning Track

To improve the quality of step scan of the reticle stage system of lithography, thus enhance the quality of the finished products of silicon wafers, the trajectory planning based on S-curve is proposed. The iterative learning control is studied, and in accordance with the limitations under specific part of the system becomes deterioration in the general global iteration algorithm, the iterative learning controller is optimized in segmentally by adopting segmented iterative compensation strategy. The simulation indicates that iterative learning control satisfies practical demands for the system; it can be used in commissioning of the reticle stage system.

Lithography Reticle stage Step scan S-curve Segmented iterative learning control

国家重大科技专项基金资助项目(编号：2009ZX02207)。

魏凯(1990-)，男，现为哈尔滨工业大学控制科学与工程 专业在读硕士研究生；主要从事超精密伺服运动控制方面的研究。

TP273+.3

A

10.16086/j.cnki.issn1000-0380.201505005

修改稿收到日期：2014-08-25。