指针式仪表总体最小二乘图像校验算法

张远辉 张 鼎 许 昌 谢 波

(中国计量学院机电工程学院，浙江 杭州 310018)

指针式仪表总体最小二乘图像校验算法

张远辉 张 鼎 许 昌 谢 波

(中国计量学院机电工程学院，浙江 杭州 310018)

为了解决传统指针式仪表人工校验准确率低的问题，提出了一种基于计算机视觉的指针式仪表校验算法。将仪表图像由RGB颜色空间模型转换到HSV颜色空间模型，利用仪表盘指针的颜色特征信息提取指针；并采用总体最小二乘法拟合指针中心轴直线；通过腐蚀膨胀提取仪表刻度，计算指针与刻度的偏差，从而判断仪表是否合格。校验试验结果表明,该算法可靠性高、鲁棒性强、校验准确率高。

指针式仪表 计算机视觉 HSV颜色空间模型 总体最小二乘法 点到线距离

0 引言

利用计算机视觉辅助检测技术对产品的尺寸和角度进行检测，能克服传统人工目视检测过程中诸如人眼的检测精度有限、检测效率不高等缺点，加快检测速度。图像检测的一种典型应用是指针式仪表的指针角度检测，该类仪表在出厂前需要对其各项功能尤其是指针所指向的角度进行严格的校准。目前，常见的指针式仪表校验的方法有：①用Sobel垂直算子边缘提取并通过Hough变换获取指针旋转中心，再利用指针图像向旋转中心进行投影来检测指针位置的方法[1]；②利用动态滑动窗口算法确定目标感兴趣区域(region of interest，ROI)，利用小波变换提取ROI区域中指针的特征信息，从而计算其旋转角度的检测方法[2]；③先使用HSI颜色模型，通过色调H和饱和度S分量作为特征参数分割图像、消除阴影，提取出没有干扰的理想目标，再细化腐蚀目标和Hough变换直线检测计算旋转角度的方法[3]等。目前，对于仪表指针的校验往往是选取指针在运动过程中不同位置的两张图像，通过分析两张图像中的指针位置姿态信息计算旋转夹角，并与标准角度作对比[4]。将图像中识别的指针旋转角度转化为实际指针旋转角度，需要借助摄像机标定参数来进行换算。由于摄像机和待测仪表盘之间的位置不固定，因此为避免反复的摄像机标定过程，本文采用图像中指针位置与图像中表盘刻度的偏差来校验仪表。由于Hough变换进行直线检测的计算量较大，影响检测效率，本文采用总体最小二乘法拟合直线的方法来处理指针中心轴线的识别问题。

1 算法框图

基于图像总体最小二乘的指针式仪表校验算法的基本步骤如下。

① 图像采集：利用摄像机采集待校验仪表指针指向主要刻度的若干幅图像。

② 指针提取：转换图像的颜色空间模型，从RGB颜色空间模型转换成色调-饱和度-亮度(hue-saturation-value，HSV)颜色空间模型，利用色调H与饱和度S分量作为特征参数提取指针区域。

③ 指针直线拟合：把提取得到的指针区域上的所有点作为特征点，利用总体最小二乘法将指针拟合成一条直线，该拟合直线为指针的中心轴线。

④ 仪表刻度提取：利用表盘的颜色特征提取仪表主要刻度区域，根据刻度区域中的所有特征点计算每个刻度的质心。

⑤ 校验：根据指针拟合中心轴线的相关参数，计算其到仪表主要刻度的偏差。若此偏差在误差允许范围内，则判定仪表通过校验，反之则判定该仪表不合格。

指针式仪表校验算法框图如图1所示。

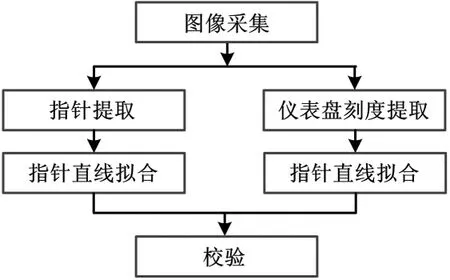
图1 指针式仪表校验算法框图

2 指针提取

仪表盘彩色图像中，指针颜色呈红色，其颜色特征明显区别于表盘其他区域。在RGB颜色空间模型下，颜色是由RGB三原色以不同比例相加产生。由于指针并非纯色，根据RGB颜色空间中的R特征提取指针效果并不理想。

HSV颜色空间[5-6]是均匀的颜色空间，采用三个颜色特征分量：色调H、饱和度S、亮度V，反映了人的视觉对颜色的感觉。色调H表示色彩的基本属性，饱和度S表示色彩的纯度，亮度V表示颜色的强度与图像的彩色信息无关。鉴于HSV颜色空间模型，可将图像的彩色信息通过色调H与饱和度S更细致的描述，并且对RGB三原色的区分度更大。因此，将RGB颜色空间模型转化到HSV颜色空间模型，用色调H与饱和度S当作特征参数来进行阈值分割，提取比较理想的指针特征。

由RGB颜色空间模型到HSV空间模型的转换公式如下：

V=Cmax

(1)

(2)

(3)

式中：Cmax=max(R,G,B)，代表RGB颜色空间中R、G、B三个分量中最大的值；Cmin=min(R,G,B)，代表RGB颜色空间中R、G、B三个分量中最小的值；NAN表示未定义；R、G、B的取值范围是[0,255]；色调H的取值范围是[0,360]；饱和度S的取值范围是[0,1]。

指针提取和直线拟合结果如图2所示。

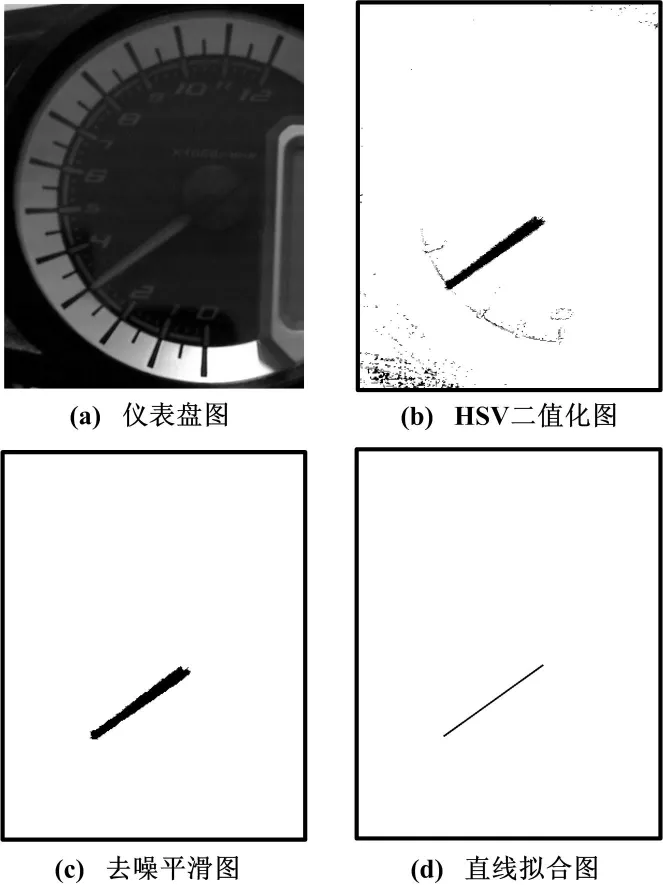
图2 指针提取和直线拟合结果

本文示例的仪表盘如图 2(a)所示，指针颜色为红色，其色调H和饱和度S与表盘差异明显。将图像RGB颜色空间模型转换成HSV颜色空间模型，选定色调H与饱和度S合适的阈值区间对图像进行二值化。计算公式如下：

(4)

式中：f(x,y)为二值化图像在点(x,y)处的像素值；h为色调值；h1、h2为色调阈值；s为饱和度值；s1、s2为饱和度阈值。

阈值可以通过计算直方图得出，二值化结果如图 2(b)所示，指针被提取出来，但是存在一定的噪声干扰。为了去除二值图像的噪声，对二值图像寻找轮廓，并计算每个轮廓的面积。由于噪声与指针的像素面积差距很大，通过设定面积阈值剔除噪声。再采用5×5模板对图像先膨胀后腐蚀，平滑后的图像如图 2(c)所示，此时剔除噪声后，指针提取比较理想。

3 指针中心轴线拟合

本文利用总体最小二乘法[7-8]拟合仪表盘指针的对称中心轴线。该方法的主要优点是直线拟合精度较高且计算量小。总体最小二乘法拟合直线示意图如图3所示。

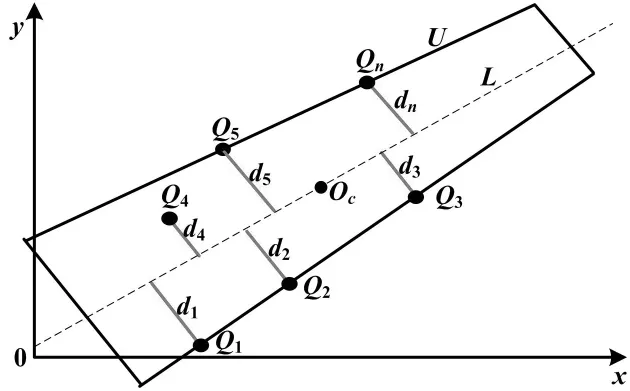
图3 总体最小二乘法拟合直线示意图

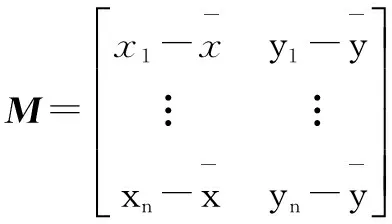
图3中，U为仪表指针区域；Q1=(x1,y1)T,Q2=(x2,y2)T,…,Qn=(xn,yn)T为U的特征点；直线L:Ax+By-C=0(图中点划线所示，A,B,C为待定系数)是通过总体最小二乘法拟合的直线。直线L求解方法如下。

二维平面上特征点Qi=(xi,yi)T到直线L的距离平方di为：

(5)

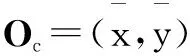
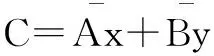
(6)

‖(u1σ1v1T+u2σ2v2T)t‖2

(7)式中：u1、u2为矩阵M奇异值分解的正交的n×1的列向量；σ1、σ2为矩阵M奇异值分解的奇异值，其中σ1≥σ2；v1、v2是2×1的列向量。

如果把M看作是一个运算符，则Mt表示对t的一个变换过程。当t等于向量v2时，即最小奇异值σ2对应的右奇异向量，‖Mt‖取得最小值，于是可求解得到L直线方程的系数A、B，此拟合直线为指针的对称中心轴线，如图 2(d)所示。

4 仪表刻度提取

计算指针与刻度的偏差，不仅需要指针的拟合直线，还需要提取仪表盘各个刻度(如图 2(a)所示)。仪表盘外圈刻度背景为亮白色，根据这个特征，刻度提取具体步骤如下。

首先将图像转换成灰度图像，计算公式如下：

Y=0.299R+0.587G+0.114B

(8)

式中：R、G、B为图像RGB颜色空间中各分量的值；Y为转换后的灰度图像分量值。

根据仪表盘外圈刻度背景为亮白色这一特征信息，对灰度图像进行二值化，排除仪表图像中大部分与刻度无关的信息。由于二值化图像中存在噪声，并且外圈刻度背景是一个面积较大的整体，通过计算轮廓的面积剔除噪声，结果如图4(a)所示，此时刻度背景被提取出来，且各个白色凹陷部分即为所需要获取的刻度。

采用9×9模板对刻度背景图进行先膨胀后腐蚀处理，确保刻度背景的凹陷部分被填充，如图4(b)所示。将被填充前后的两幅刻度背景图像作绝对值相减，即可得到理想的仪表盘刻度，如图4(c)所示。计算每个刻度的质心[9]，计算公式为:

(9)

式中：xc、yc为刻度的质心；xi、yi为刻度像素点的横坐标和纵坐标。

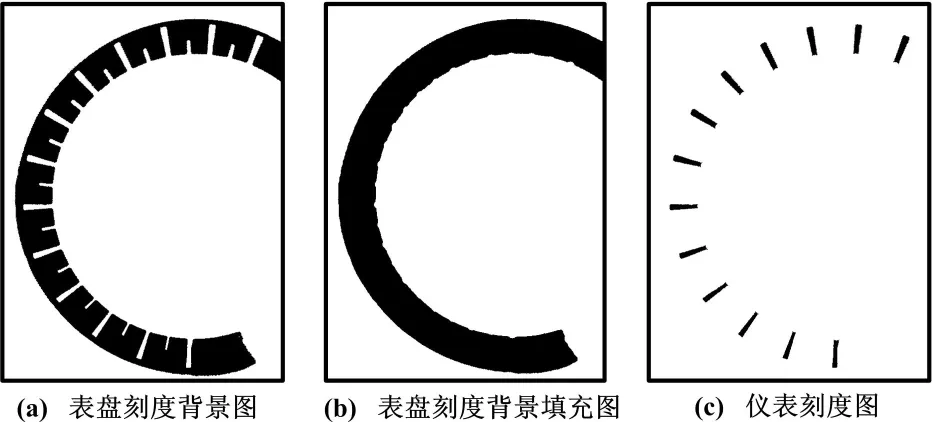
图4 仪表刻度提取结果

5 指针校验

通常指针式仪表的校验，采用图像处理计算指针角度与实际标准角度作对比的方法。但在拍摄过程中，由于摄像头的光轴与仪表表面不能保证绝对垂直，并且也存在沿摄像机光轴垂直方向的偏移，这些都需要通过摄像机标定得以修正。所以本文采用计算指针到仪表刻度偏差的方法来避免摄像机标定的过程。通过计算刻度的质心与指针拟合直线的距离，判断此距离是否在误差允许范围内，从而实现仪表校验。

指针到刻度的误差距离计算示意图如图5所示。

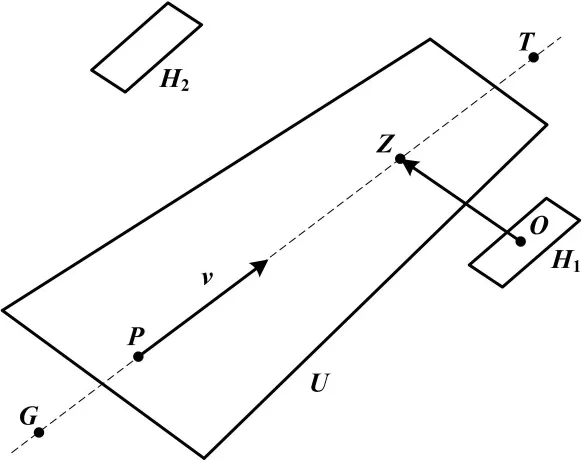
图5 指针到刻度的误差距离计算示意图

图5中，v为指针U的拟合中心轴直线GT的单位方向向量，P=(x,y)T为GT上的一个点，二维平面上的直线方程可以描述为GT:X=P+kv，k为任意实数，X为直线上的任意点。H1、H2为仪表的刻度，点O为刻度H1的质心，由O向直线GT做投影，垂足为Z，矢量n=OZ为直线GT过点O的法向量：

n=(P-O)-[(P-O)v]v

(10)

点O到直线GT的距离f[O,(P,v)]为：

f[O,(P,v)]=‖n‖

(11)

利用总体最小二乘法拟合的指针中心轴直线，通过式(11)可以求得指针到刻度的距离。根据所规定的误差标准，从而判断仪表指针是否需要重新校准。

6 试验结果

采集指针分别指向0、1 000、3 000、6 000、9 000和12 000 (单位为r/min)刻度的图像，每采集一幅图像后，调整一次摄像头与仪表的相对位置，每个刻度分别采集10幅图像。由式(7)根据总体最小二乘法可得到指针的拟合直线，由式(11)可计算得到指针与刻度的距离偏差。通过与对应的标准值作比较，当误差小于θ时(θ值可根据该仪表所需要达到的精度设定)，则认为仪表指针工作正常；反之则提示出错信号，此仪表指针需要重新校准。

为了验证本文方法的合理性，将指针与刻度的距离转换为更加直观的指针与刻度的偏差角度。用所有刻度质心点拟合一个“刻度圆”，其圆半径即为刻度质心到仪表旋转中心的距离。根据刻度圆半径和指针到刻度的偏差距离，通过反正切函数tan-1计算指针与刻度的偏差角度，计算同一刻度拍摄得到的10幅图像的偏差角度与标准差。使用“细化+Hough”方法作为本文方法的对照试验。该方法首先对图像进行指针区域提取；再利用改进鲁棒性能的Zhang并行快速细化算法[10]将指针细化为骨骼线；然后通过多分辨率Hough变换[11]提取指针骨骼线直线，计算指针与刻度的距离偏差从而得到对应的偏差角度，并计算标准差。对比结果如表 1所示。细化+Hough方法作为指针式仪表检测常用的算法，具有准确率高的特点。当提取到的指针存在少许毛刺时，对细化产生干扰导致Hough变换计算得到的偏差角度波动较大。

由表1发现，本文方法得到的指针与刻度的距离转转换成指针与刻度的偏差角度后，其偏差角度小于1°，且偏差角度的标准差较小，因此本文方法总体上优于细化+Hough方法。在计算量方面，本文方法校验单幅仪表图像的平均处理时间为0.79 ms，细化+Hough方法为13.50 ms，测试条件是Win7系统，Visual C++2010环境，CPU主频为2.20 GHz，内存为2 GB。细化+Hough方法的运算时间大大高于本文方法。一方面是由于Hough变换提取直线前需要对图像进行细化处理，改进鲁棒性能的Zhang细化算法采用更多的判断条件以克服经典Zhang细化算法在对角线位置(比如45°或者135°位置的指针)骨骼线过度收缩的缺陷问题；另一方面是由于Hough变换采用多分辨率角度测量，设定其运算精度为0.01°，计算量也较大。综上所述，本文提出的指针式仪表校验方法精度高，运算量小且具有较强的鲁棒性。

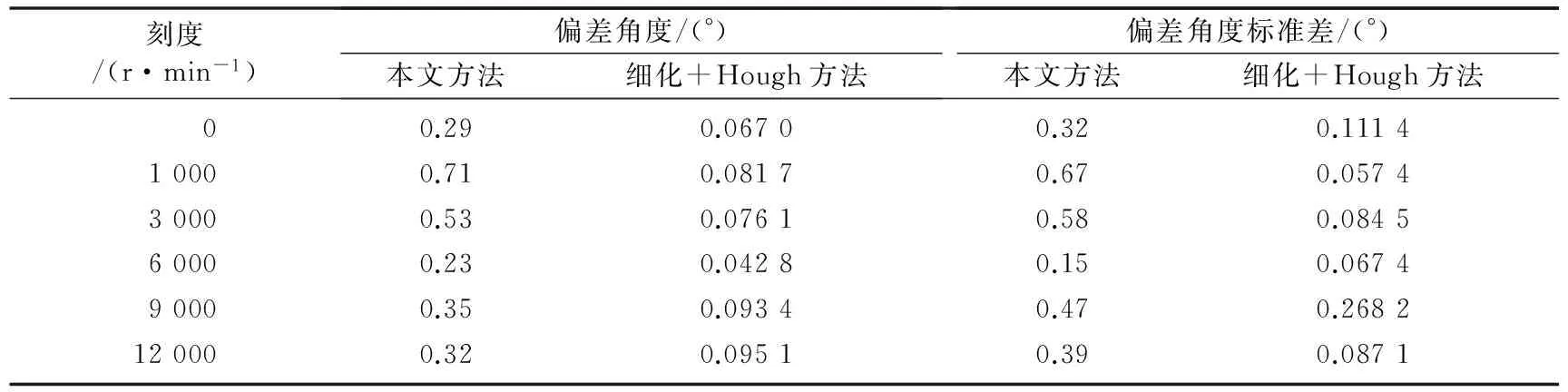
表1 指针与刻度偏差角度与标准差

7 结束语

本文设计的指针式仪表校验算法，在HSV颜色空间模式下进行指针提取，采用总体最小二乘法拟合指针中心轴线，计算指针相对于刻度的偏差,从而判定仪表指针是否工作正常。算法有如下特点：①算法主要针对于仪表指针相较于表盘中其他区域色调与饱和度存在明显差异，而对表盘形状没有要求；②利用总体最小二乘法拟合指针直线不仅有较高的可靠性，而且相比于Hough变换减少了计算量；③通过计算指针与刻度的距离来判断仪表指针是否工作正常，可以避免图像采集过程中摄像机标定过程。

对于常用指针式摩托车仪表的试验结果表明，该算法可靠性高、鲁棒性强、校验准确率高，因此具有广阔的应用前景。

[1] 李栋,杨志家.基于机器视觉的指针仪表识读方法[J].仪表技术与传感器,2012(10):31-34.

[2] Jaffery Z A.Architecture of noninvasive real time visual monitoring system for dial[J].Sensor,2013,13(4):1236-1244.

[3] 周泓,徐海儿,耿晨歌.基于HSI模型和Hough变换的指针式汽车仪表自动校验[J].浙江大学学报:工学版,2010,44(6):1108-1112.

[4] 张冀,王俊宏,尉迟明.基于计算机视觉的汽车仪表指针检测方法[J].计算机工程与科学,2013,35(3):134-139.

[5] 常巧红,高满屯.基于HSV色彩空间与数学形态学的车牌定位研究[J].图学学报,2013,34(4):159-162.

[6] James I.Face image retrieval with HSV color space using clustering techniques[J].The SIJ Transactions on Computer Science Engineering & its Applications,2013,1(1):17-20.

[7] 吴梅,王瑞,李琦.基于总体最小二乘法的表盘图像中心点提取[J].自动化与仪表,2013,28(10):53-56.

[8] Lee G,Barlow J L.Two projection methods for regularized total least squares approximation[J].Linear Algebra and its Applications,2014,461:18-41.

[9] 史少龙,尹达一.改进型灰度质心实时算法研究[J].光电工程,2013,40(12):18-24.

[10]Tarabek P.A robust parallel thinning algorithm for pattern recognition[C]//7th International Symposium on Applied Computational Intelligence and Informatics(SACI).Romania:IEEE,2012:75-79.

[11]Woodford O J,Pham M T,Maki A.Demisting the hough transform for 3D shape recognition and registration[J].International Journal of Computer Vision,2014,106(3):332-341.

Image Calibration Algorithm Based on Total Least Squares Method for Pointer Instruments

To solve the problem of low accuracy for traditional pointer instruments caused by manual calibration, the verification algorithm based on computer vision for pointer instrument is proposed. The image of the instrument is transformed from RGB color space model into HSV color space model, the pointer is extracted by adopting the color characteristics of the panel pointer, then the total least squares method is used to fit the central axis of pointer; and the scale of the instrument is extracted through eroding and dilating algorithm, the deviation between the pointer and scale is calculated, thus to judge if the instrument is qualified or not. The result of calibration experiments indicates that this algorithm is reliable and robust; the calibration accuracy is high.

Pointer instrument Computer vision HSV color space model Total least squares method Point-to-line distance

国家自然科学基金资助项目(编号：61302191)；

浙江省教育厅科研基金资助项目(编号：Y201224542)。

张远辉(1982-)，男，2009年毕业于浙江大学控制理论与控制工程专业，获博士学位，讲师；主要研究方向为机器人智能控制、计算机视觉和图像处理。

TP391

A

10.16086/j.cnki.issn1000-0380.201505019

修改稿收到日期：2014-10-29。