基于参数样条的轮式车跟踪控制策略
2015-06-15李年裕王志辉李兆耿
李年裕, 王志辉, 李兆耿, 田 鹏
(1. 装甲兵工程学院控制工程系, 北京 100072; 2. 装甲兵学院装备运用系, 安徽 蚌埠 233051; 3. 63729部队, 山西 太原 030027)
基于参数样条的轮式车跟踪控制策略
李年裕1, 王志辉1, 李兆耿2, 田 鹏3
(1. 装甲兵工程学院控制工程系, 北京 100072; 2. 装甲兵学院装备运用系, 安徽 蚌埠 233051; 3. 63729部队, 山西 太原 030027)
以某6×6无人轮式车为对象研究跟踪控制策略,使其能够自主跟踪引导车的运动轨迹,并与引导车保持一定的安全距离。首先研究了采用参数样条曲线建立柔性虚拟曲杆模型的方法,并提出了虚拟曲杆的弹性力控制策略;然后又引入一种轨迹跟踪控制律,实现了对6×6无人轮式车跟踪运动的双闭环控制。最后通过Matlab仿真和实车试验对该控制策略进行了验证,结果表明:该控制策略能够保证车辆稳定行驶,并有效地提高了跟踪精度。
轮式车;跟踪控制; 参数样条;虚拟曲杆
车辆跟踪控制策略的研究具有重大的军事和社会经济意义。近年来,欧洲一直在研究“公路列车”技术[1],美国为未来国防而研制的Demo-2和Demo-3[2]等都具有车辆自动跟踪功能。
车辆自动跟踪技术是智能交通系统(Intelligent Transport System, ITS)研究中的重要内容,它能使后车(Follower)在一定安全距离下自动紧密跟随前车(Leader)的运动轨迹行驶,兼顾了交通效率和安全2个方面,具有广阔的应用前景[3-4]。现有的车辆自动跟踪系统控制策略有3类:1)直接以前车为目标点进行跟踪;2)以后车前方的一个虚拟点为目标点进行跟踪;3)以前车后方的一个虚拟点为目标点进行跟踪。
若直接以前车为目标点进行跟踪,在弯道行驶时,后车因前车转弯而立即转弯,可能会撞向路边或其他车辆。Pham[5]模仿人的驾驶习惯,定义了一个后车运动方向上的虚拟点作为目标点,该点与后车转角有角度偏差,并与后车车头方向中心保持固定距离,实验结果表明:以后车前方的一个虚拟点为目标点进行跟踪,无法实现准确跟踪前车轨迹。Ng等[6-7]借鉴欧洲Chauffeur项目[8]中的电子拖杆跟踪系统,提出了“虚拟拖杆模型(Virtual Trailer Link Model)”,即前、后车由2根铰接的虚拟直拖杆相连,两杆之间的角度可以变化,杆的当前构型则通过前车当前位姿与历史位姿进行贝叶斯估计得出[7],后车不直接跟踪前车,而是跟踪虚拟拖杆的末端,实验结果表明:这种跟踪策略有效地减小了跟踪误差。
在“虚拟拖杆”的基础上,张晓媚等[9-10]提出了“柔性虚拟曲杆模型”:虚拟曲杆就是前、后两车之间的轨迹,长度根据车距可伸缩,前车转弯时虚杆对后车有延时力的作用。张晓媚等采用系列短圆弧来描述柔性虚杆的形态,与文献[6-7]中虚拟拖杆模型相比,采用短圆弧建立的柔性虚杆模型跟踪精度更高;但是短圆弧法未能很好地保证航向角连续,拟合前车轨迹的准确性也欠佳。
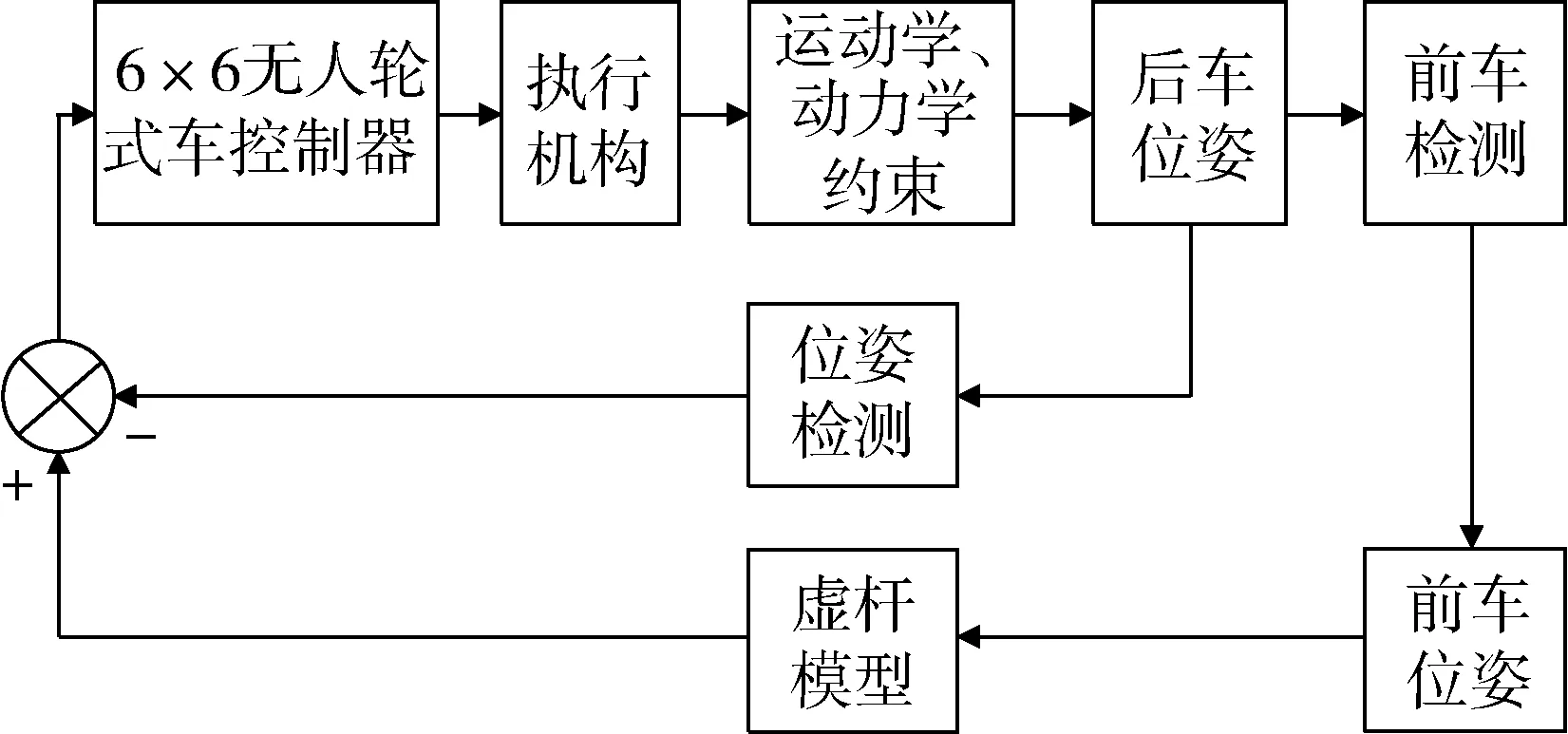
为此,笔者以某6×6无人轮式车(图1)为控制对象,拟采用参数样条曲线建立柔性虚拟曲杆模型,以期能够更加准确、平滑地描述前车行驶过的轨迹,并在此基础上引入虚拟弹性力的控制,再和一种轨迹跟踪控制律共同作用,实现对6×6无人轮式车跟踪运动的双闭环控制,最后通过Matlab仿真和实车试验对该控制策略进行验证。

图1 6×6无人轮式车
1 基于参数样条的柔性虚杆模型
在跟踪过程中,后车每一采样时刻利用传感器对前车的位置进行一次检测,在全局坐标系下获得一系列前车的轨迹点Pi(xi,yi,θi)(i=1,2,…,n),其中:xi、yi为车辆位置横、纵坐标;θi为车辆姿态角。在传统的跟踪方法中,后车直接以这些离散点为跟踪目标,难以确保后车运动的平滑性和准确性。
前、后车跟踪坐标系如图2所示,在全局坐标系下分析后车对前车的跟踪。为了使后车平滑地沿着前车轨迹运动,需要利用采样得到的离散点准确拟合前车轨迹,根据柔性虚拟曲杆的思想[9-10],需要利用一种合理的曲线来建立虚拟曲杆模型,由虚拟曲杆“拉动”着后车,使后车跟踪着虚杆的末端运动。

图2 前、后车跟踪坐标系
前车轨迹拟合的方法一般有逼近法和插值法,由于逼近法所构建的曲线不一定会经过这些点,构造的曲线曲率可能小于车辆的转弯半径,使得无人车的行驶出现问题,因此采用插值法进行前车轨迹拟合。选取插值曲线有2种极端情况:1)在每对{Pi,Pi+1}(i=1,2,…,n-1)间进行线性插值,在插值点附近会出现拐折现象;2)采用高次多项式对轨迹点进行插值,当数据点增加时,多项式次数会增加,可能会产生震荡,出现“龙格现象”。
为了避免分段线性插值和单一的高阶多项式插值的缺陷,笔者考虑采用分段多项式函数进行插值,通过大多数应用发现:三次样条曲线是折中选择。因此,本文采用如下样条曲线:对于前车轨迹在Pi(xi,yi)与Pi+1(xi+1,yi+1)两点间的形态,采用三次样条曲线进行插值[11],同时为了保证样条曲线在各点处均有一阶导数连续,在每个插值点附加边界条件。但是,传统的样条曲线拟合会出现如下2个问题:
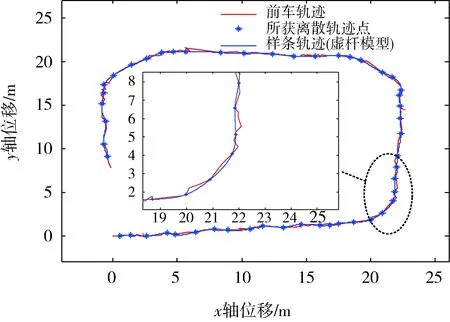
1) 对于点集Pi(xi,yi),使用样条函数拟合曲线的必要条件是x1 2) 如果点集Pi(xi,yi)中存在(xi,yi)和(xj,yj)2个点,其中xi=xj,即有一段垂直于x轴的路径,此时曲线的斜率为无穷大,无法使用y=f(x)的形式对此进行描述。 为此,可以采用参数样条的方式来对轨迹点进行拟合,通过合理地选择参数,可以使参数曲线对型值点的方向不敏感[12-13]。 对于点集Pi(xi,yi),每2个点(xi,yi)、(xi+1,yi+1) (i=1,2,…,n-1)间都构成一段曲线lk,以参数方程的形式写成如下的形式: (1) 式中:0≤t≤ti,为参数,这里采用弦长作为t值,其中ti为连接两点间直线段长度。 对于(xi,yi)、(xi+1,yi+1)间的某一点(x,y),可以得到该点与本段起点的直线距离,即弦长 (2) 对于每一个点,弦长与点的位置对应,设tmax为本段最大弦长,则 (3) 在[0,tmax]中的每一个值,都可以找到一个对应点。而从(xi,yi)指向(xi+1,yi+1)的曲线中,弦长t总是单调增加的。 以lk段xk(t)方程为例,有 xk(0)=a1=xi, (4) (5) (6) (7) 于是可以得到 (8) (9) 从而有 0≤t≤ti。 (10) (11) (12) 同理,可以解得yk(t)参数方程,从而建立点集Pi(xi,yi)的参数样条插值曲线: {lk}={xk(t),yk(t)}|k=1,2,…,n-1。 (13) 式(13)为全局坐标系下前车轨迹的解析表达式,描述了本文所使用的虚拟曲杆形态(图3)。后车的航向角表达式为 (14) 图3 虚拟曲杆形态 如此描述的轨迹保证了其上每一点的一阶导数都是连续的,即保证了前车的轨迹和航向角也是连续的,为后车更加平滑、准确地跟踪前车提供了保证。 通过弧长公式可以得到前后车之间的轨迹长度,即虚拟曲杆的长度为 (15) 为了便于车载工控机运算处理,应用牛顿-柯特斯公式对式(15)进行求解,得到 (16) 至此得到虚拟曲杆的解析表达式和虚拟曲杆的长度,该曲杆模型完全拟合了全局坐标系下前车的历史轨迹。 实际上,当车辆跟踪系统处于稳定状态时,后车应该与前车保持一定安全距离,紧密地跟随前车运动,后车的线速度等于前车的线速度。类似于北京加长版的公交车(图4)中间部分的弹性连接,在柔性虚杆模型的跟踪系统中,改变前车的运动状态会导致柔性虚杆伸缩弯曲,虚杆的内部作用力随之变化,进而改变后车的运动状态,使整个系统达到平衡。 图4 北京加长版公交车 图5 跟踪系统模型 跟踪系统模型如图5所示,将中间的柔性虚拟曲杆应用弹簧的物理性质,弹性系数为k,则虚杆的虚拟力为 F=k(l-D), (17) 式中:l为虚杆的当前长度; (18) 为动态安全距离,即虚杆的固有长度。其中:al、af分别为前、后车加速度;vl、vf分别为前、后车速度;D_static为前后车静止时的安全距离。 式(18)可以理解为虚杆固有长度等于前、后车静止时的安全距离、后车正常制动距离与后车反应时间行驶距离之和减去前车制动距离。 后车在虚杆虚拟力的作用下产生的加速度为 (19) 式中:mf为后车的质量。k、mf取值只要让后车速度尽量平滑即可。 后车在下一采样时间将要运动的距离为 (20) 式中:T为采样时间。 后车的速度变为 vfnew=vf+afT。 (21) 后车的速度不能取负值,如果为负值,则直接赋值0。后车沿着虚拟曲杆将要运动到A′(xA′,yA′,θA′),可以近似认为 (22) 至此得到后车在柔性虚拟曲杆拉动下的速度、加速度信息。在理想情况下,6×6无人轮式车可以按照该命令完成跟踪运动。但是在实际系统中,6×6无人轮式车受自身运动特性的限制,同时也存在干扰信息,故需要针对6×6无人轮式车设计一个轨迹跟踪控制律来收敛位姿误差,本文采用控制律[14]如下: (23) 李辉等[14]已经验证该系统是稳定的,式(23)中采用vr=(vf+vfnew)/2,ωr=ωfnew可以使后车运动更加平滑。 6×6无人轮式车跟踪控制系统的整体框架如图6所示,系统包括2个反馈环:外环是通过车载传感器对前车进行位姿检测和虚拟曲杆模型控制,使后车沿着前车轨迹运动;内环是6×6无人轮式车自身的位姿检测与控制,确保后车能够准确地跟踪虚杆的末端。 图6 6×6无人轮式车跟踪控制系统整体框架 利用Matlab软件对该控制系统进行仿真,为了检验本文控制算法的跟踪精度,把前车的轨迹设置成一个类似“S”型的曲线,包含了直驶、右转、左转,并与文献[10]中跟踪方法进行对比。将前车的速度设为4 m/s,安全距离设为固定值6 m,前后车初始距离设为5 m,采样周期设为0.1 s,控制参数取kx=5,ky=0.81,kα=2,kθ=1.8,k/mf=0.1。图7为采用2种跟踪跟踪控制策略仿真得到的车辆跟踪轨迹对比,可以看出:本文提出的跟踪控制策略可使跟踪误差更小。图8是2种跟踪控制策略下后车航向角的变化曲线对比,可以看出:在本文的跟踪控制策略下,后车航向角变化和前车基本一致,只是具有延时效应,这正符合正常车辆跟踪的特征,说明基于三次参数方程建立的虚杆模型能够更好地保证车辆的航向角连续。 图7 2种跟踪控制策略下车辆跟踪轨迹对比 图8 2种跟踪控制策略下后车航向角的变化曲线对比 图9为实车跟踪试验情形,其中:有人驾驶车作为前车;6×6无人轮式车作为后车。前后车装有GPS惯性导航组合装置,可记录前后车的轨迹,由于架设了差分GPS,因此定位精度在0.1 m以下。 图9 实车跟踪试验 4.1 “虚杆”生成试验 后车保持不动,采用参数样条法拟合前车运动的离散轨迹点,不断地生成“虚杆”。在全局坐标系下记录前车轨迹、离散轨迹点、“虚杆”曲线,如图10所示,其中:蓝色星点是后车获取的前车运动的离散轨迹点;蓝线是算法生成的样条轨迹,亦即“虚杆”轨迹;红线是前车的轨迹,由GPS惯导装置直接记录得到。 图10 “虚杆”生成试验 由图10可见:由离散点生成虚杆的轨迹和前车GPS记录的轨迹基本一致,说明基于参数样条的虚杆模型能够有效地描述前车的运动轨迹,且轨迹光滑,符合车辆运动的特点,为后车的跟踪控制提供了必要条件。 4.2 跟踪试验 在6×6无人轮式车内装有车载工控机,根据本文提出的跟踪控制方法,采用C++builder设计了相应的控制软件。图11记录的是跟踪控制系统进行弯道试验的结果,其中:红色是虚杆的轨迹;蓝色是后车跟踪的轨迹。 图11 跟踪控制系统弯道试验结果 从图11可以看出:6×6无人轮式车有效地完成了对虚杆末端的跟踪,运动路线基本上与虚杆轨迹相符,实际误差在0.5 m范围内;在跟踪过程中,平台起步平稳,直行和转向控制平稳,并在预期点停车,达到了预期的跟踪效果。 本文针对6×6无人轮式车的轨迹跟踪问题,研究了用参数样条曲线描述柔性虚拟曲杆形态的方法,并在参数样条建立的虚杆模型基础上,给出了一种双闭环的跟踪控制策略。文中提出的采用参数样条拟合曲线的方法能够较好地拟合前车的轨迹点并保证了航向角的连续性,使后车的跟踪运动更加平滑,同时解决了一般样条函数拟合时对型值点方向不敏感的问题,能够很好地描述各种形态的轨迹曲线。仿真结果和实车试验结果表明:本文研究的跟踪控制策略是可行的。 前车行驶过的轨迹对于后车一般来说是可行的,但本文没有考虑出现运动障碍物等突发情况。下一步,针对可能出现的运动障碍物,后车需要能够规划新的运动轨迹,以做出相应的避障和应急控制。 [1] 汤水. “公路列车”:让汽车自动驾驶[J]. 发明与创新,2011(5):35-36. [2] Yang H W. Tracking Control of a Nonholonomic Mobile Robot by Hybrid Feedback and Neural Dynamics Techniques [D]. Guelph,Canada: University of Guelph, 2003. [3] Mo Y K, Deng J. Fundamentals of Intelligent Public Transportation Dispatching Systems Planning[C]∥Proceedings of 2009 Second ISECS International Colloquium on Computing, Communication, Control, and Management(CCCM 2009). Piscataway, NJ, USA: IEEE Computer Society, 2009:41-44. [4] Gu J S, Yi S, Yi K. Human-centered Design of a Stop and Go Vehicle Cruise Control[J]. IEEE International Journal of Automotive Technology, 2006, 7(5):619-624. [5] Pham H.Development and Implementation of a Trajectory Planner and a Tracking Controller for an Autonomous Vehicle[D]. Singapore: School of Electrical and Electronic Engineering, Nanyang Technological University,2001. [6] Ng T C. Autonomous Vehicle Following: a Virtual Trailer Link Approach[D]. Sinapore: Sinapore Institute of Manufacturing Technology, Nanyang Technological University, 2009. [7] Ng T C, Adams M D, Guzman J I. Bayesian Estimation of Follower and Leader Vehicle Poses with a Virtual Trailer Link Model[J]. International Journal of Robotics Research, 2008, 27(1):91-106. [8] Borodani P. Full Automatic Control for Trucks in a Tow-bar System[C]∥Proceedings of International Symposium on Advanced Vehicle Control. Piscataway, NJ, USA:IEEE, 2000:131-138. [9] 张晓媚, 陈伟海, 刘敬猛. 基于柔性曲杆的车辆跟踪算法设计与实现[J]. 北京航空航天大学学报,2011,37 (3):789-194. [10] 陈伟海, 张晓媚, 吕章刚. 适用于独立式车辆自动跟踪的力延时柔性虚杆建模[J]. 机器人,2011,33(5):599-605. [11] Howard T M, Kelly A. Trajectory Generation for Car-like Robots Using Cubic Curvature Polynomials[J]. Field and Service Robots, 2001, 3(2):19-23. [12] 苏步青. 关于三次参数样条曲线的一些注记[J]. 应用数学学报, 1976, 1(1):49-58. [13] 苏步青. 关于三次参数样条曲线的一些定理[J]. 应用数学学报, 1977, 1(1):50-54. [14] 李辉, 李年裕, 张豫南. 一种无人地面车的轨迹跟踪控制方法[J]. 装甲兵工程学院学报, 2012, 10(5):80-84. (责任编辑:尚彩娟) Tracking Control Strategy for Wheeled Vehicles Based on Parameter Spline LI Nian-yu1, WANG Zhi-hui1, LI Zhao-geng2, TIAN Peng3 (1. Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2. Department of Equipment Application, Academy of Armored Forces, Bengbu 233051, China; 3. Troop No.63729 of PLA, Taiyuan 030027, China) The paper investigates the tracking control strategy for 6×6 unmanned wheeled vehicle to make it track the trajectory of the leader vehicle precisely under the condition of keeping a safe distance. Firstly, the method of establishing a flexible virtual curved bar model with parameter spline curve is studied and a control strategy based on virtual curved bar elastic force is proposed. Then a trajectory tracking control law is introduced to realize the double closed loop control of 6×6 unmanned wheeled vehicle’s tracking motion. Finally the control strategy is verified by Matlab simulation and real vehicle test. The results show that the vehicle tracking control strategy can guarantee the stability of the vehicle motion and can effectively improve the tracking precision. wheeled vehicle; tracking control; parameter spline; virtual curved bar 1672-1497(2015)04-0062-06 2015-04-08 军队科研计划项目 李年裕(1968-),男,副教授,博士。 TP275 A 10.3969/j.issn.1672-1497.2015.04.013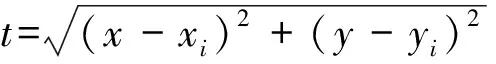

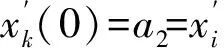

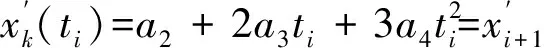
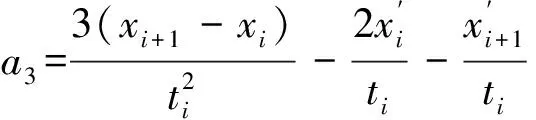
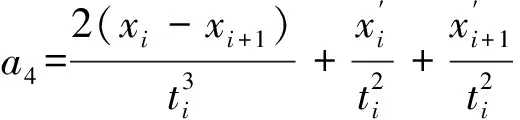

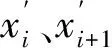


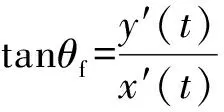

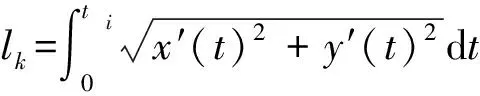

2 基于曲杆虚拟弹性力的控制算法


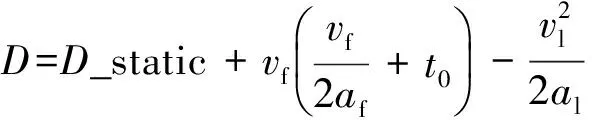
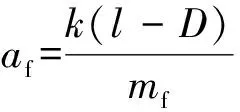



3 跟踪策略仿真验证
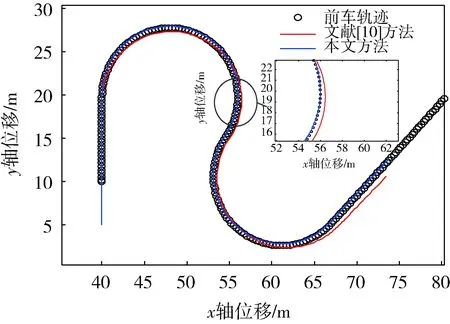
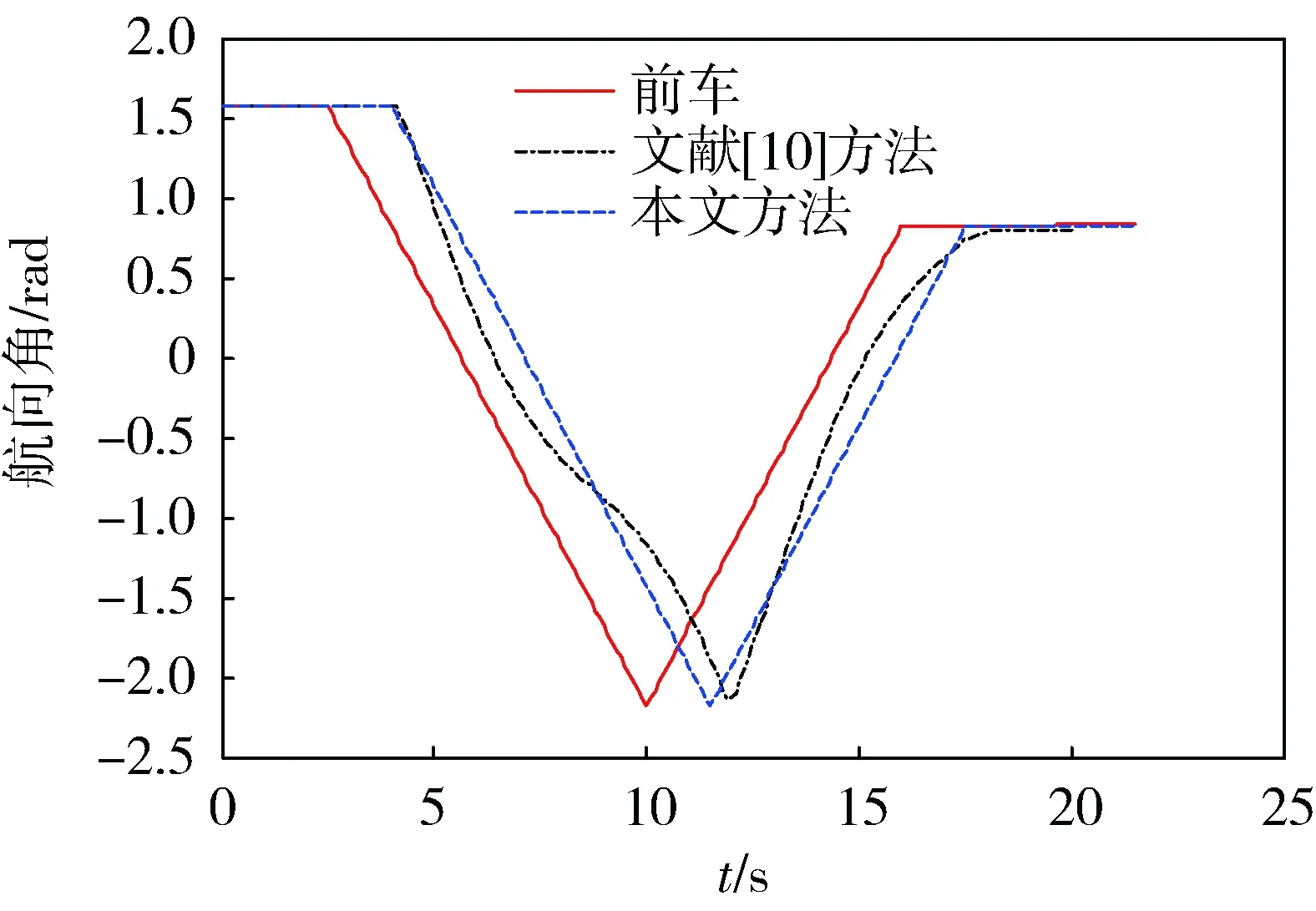
4 实车试验

5 结论
