渐进独立重尾索赔下延迟索赔风险模型的精细大偏差

乔克林，张 娟，刘琼琼

(延安大学数学与计算机科学学院，陕西延安716000)

渐进独立重尾索赔下延迟索赔风险模型的精细大偏差

乔克林，张 娟，刘琼琼

(延安大学数学与计算机科学学院，陕西延安716000)

1 引言及相关模型

服从重尾分布的精细大偏差是金融保险行业中一个重点研究的课题，它主要应用于研究极端事件导致大索赔情形下的金融保险问题。该课题的研究有利于保险公司可以做出更好的决策，降低发生经营风险的可能性。因而，有关大偏差问题的研究就显得很重要。

延迟索赔风险模型如下：

t≥0。

(1.1)

其中u>0表示保险公司的初始资本，c>0为保费率；{N(t),t≥0}是主索赔过程，N(t)=sup{i:Ti≤t}，t≥0。N(t)表示到时刻t为止主索赔发生的次数，当t→∞，有λ(t)=EN(t)→∞；主索赔额{Xi,i≥1}是非负同分布于X，分布函数为F，均值为μ1<∞。延迟索赔额{Yi,i≥1}是非负同分布与Y，分布函数为G，均值为μ2<∞。延迟索赔间隔Wi，i=1，2，…，独立同分布于W；序列{Xi，i≥1}，{Yi，i≥1}，{N(t)，t≥0}，{Wi，i=1,2,…}是两两相互独立的。

2 预备知识

若非负随机变量X不存在任何指数阶矩，即对于任意的t>0都有EetX=∞，则称它或相应的分布F为重尾分布。下面介绍几个重要的重尾分布族。

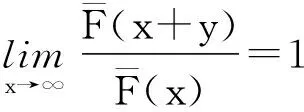
以上几种重尾分布族的包含关系[10]：

下面介绍几种随机变量之间的相依结构。

定义2.2[7，8]称随机变量序列{Xk，k≥1}渐进独立，若对于任意i≠j≥1，有

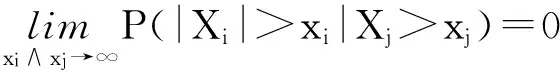
定义2.3[11]称随机变量序列{Xk，k≥1}广义负相依(ExtendedNegativelyDependent)，若存在一个正数M，使得对于每个n=1，2，…和所有x1，x2，…，xn，有

(2.1)

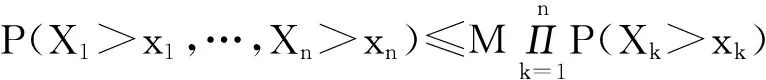
(2.2)

成立。其中(2.1)式称为下象限广义负相依(LowerExtendedNegativelyDependent)，(2.2)式称为上象限广义负相依(UpperExtendedNegativelyDependent)。

特别地，当M=1时上述的广义负相依变成了相应的负相依。

定义2.4[8]称随机变量序列{Xk，k≥1}负回归相依(NegativelyRegressionDependent)，若存在一个正数x0和c，使得

对于所有1≤i≤n，J⊂{1，2，…，n}{i}，xi>x0，xj>x0withj∈J都成立。

几种相依结构的相互关系[12]：对非负随机变量序列{Xk，k≥1}，渐进独立包含了上象限广义负相依、广义负相依、负相依和负回归相依。

定义2.5[13]令

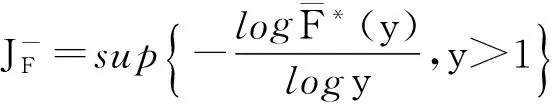
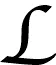
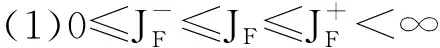
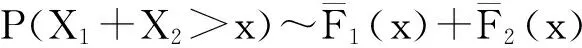
以下记

Hi=Xi+YiI(Ti+Wi≤t)，

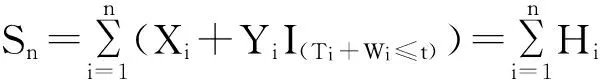
P(I(Ti+wi≤t)=1)=β(t)。

为了证明定理，我们给出在模型(1.1)下的两个引理。

引理2.4 对于随机变量序列(Zi=YiI(Ti+Wi≤t)，

i≥1}(设其共同的分布函数为E(x))，有

(2)若{Yi，i≥1}渐进独立，则{Zi，i≥1}也是渐进独立。

证明 (1)因为

(2)由{Zi=YiI(Ti+Wi≤t)，i≥1}的非负性，对于所有i≠j≥1和充分大的xi和xj，我们有

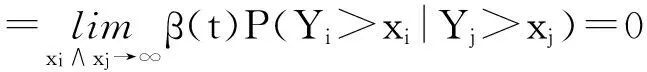
从而得证{Zi,i≥1}是渐进独立。

证明 由{Hi=Xi+Zi，i≥1}的非负性，对于所有i≠j≥1和充分大的xi和xj，我们有

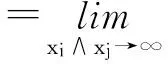
3 主要结论及其证明

(3.1)

证明 为证(3.1)式，只需证

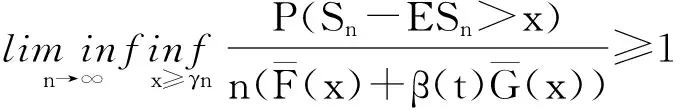
(3.2)

(3.3)

成立。

(3.2)式的证明：对任意γ>0，有

P(Sn-ESn>x)

=I1-I2。

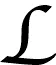
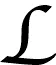
接下来估计I5。

其中倒数第二步见文献[8]中引理4.2的证明。

=0，

由上可得，当n→∞时，对x≥γn一致地有(3.3)式成立。综上，定理3.1证毕。

(3.4)

证明 对任意0<δ<1，有

P(S(t)-ES(t)>x)

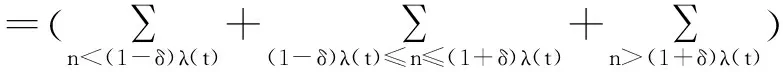
·P(Sn-ES(t)>x)P(N(t)=n)

P(N(t)=n)

=J1。

利用定理3.1的结论，对任意给定的常数γ>0，当x≥γλ(t)时，一致地有

P(N(t)=n)

(μ1+β(t)μ2)δλ(t))P(N(t)=n)

(1-δ)λ(t))，

其中a=δ(μ1+β(t)μ2)/γ。当δ→0时，

同理可得

从而

观察上式，我们可以发现x(1-a)>0，即

δ<γ/μ1+β(t)μ2。

又因0<δ<1，则0<δ<γ/μ1+β(t)μ2。

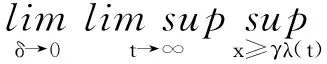
综上所述，定理3.2证毕。

上述结论分别是定理3.1和3.2的两个推论。因为上象限广义负相依可推出渐进独立。又因为上象限广义负相依、广义负相依、负相依和负回归相依都可看作渐进独立的特殊情况，所以把推论中的上象限广义负相依条件换成广义负相依、负相依和负回归相依中的任何一个，结论仍然成立。当换成是负相依时，推论就为文献[16]中的定理3.1.1和3.1.2。

[1]KlüppelbergC,MikoschT.Largedeviationsofheavy-tailedrandomsumswithapplicationsininsuranceandfinance[J].JApplProb,1997,34(2):293-308.

[2]TangQi-he,SuChun,JiangTao,etal.Largedeviationsforheavy-tailedrandomsumsincompoundrenewalmodel[J].StatProbLett,2001, 52(1): 91-100.

[3]NgKW,TangQi-he,YanJia-an,etal.Preciselargedeviationsforsumsofrandomvariableswithconsistentlyvaryingtails[J].JApplProb,2004,41(1):93-107.

[4]TangQi-he.Insensitivitytonegativedependenceofasymptoticbehaviorofpreciselargedeviations[J].Electron.J.Prob.2006,11(4):107-120.

[5]汪世界.带一致变化尾上负相依随机变量和的精细大偏差[J].合肥工业大学学报(自然科学版)，2010，33(3):464-466.

[6]LiL.Preciselargedeviationfordependentrandomvariableswithheavytails[J].StatistProbabLett,2009,79:1290-1298.

[7]MaulikK,ResnickS.Characterizationsandexamplesofhiddenregularvariation[J].Extre-mes,2004,7:31-67.

[8]GelukJ,TangQ.Asymptotictailprobabilitiesofsumsofdependentsubexponentialrandomvariables[J].JournalofTheoreticalProbability,2009,22(4):871-882.

[9]杨春芝.二元上尾独立随机变量和的精细大偏差[J].吉林化工学院学报,2014,31(3):88-89.

[10]陈琳，刘维奇.重尾分布族及其关系图[J].高校应用数学学报,2009,24(2):166-174.

[11]Block H W,Savits T H,Shaked M.Some concepts of negative dependence[J].The Annals of Probability,1982,10(3):765-772.

[12]陈忠维.相依重尾索赔下风险模型的有限时间破产概率[D].大连:大连理工大学,2013.

[13]肖鸿民，马秀芬，崔艳君，等.负相依索赔下更新风险模型的精细大偏差[J].江西师范大学学报(自然科学版),2013,37(1):12-15.

[14]Wang K Y,Wang Y B.Notes on the asympototicis of the tail probabilities of sums for egatively associated random variables with heavy tails[J].Chinese Journal of Applied Probability and Statistics,2007,23:337-344.

[15]Chen Y,Zhang W.Large deviation for random sums of negatively dependent random variables with consistently varying tails[J].Stat Prob Lett, 2007, 77: 530-538.

[16]王英.重尾相依风险模型的精细大偏差[D].兰州:西北师范大学,2013.

[责任编辑 毕 伟]

Precise Large Deviations for Delayed-Claims Risk Model under Asymptotically Independent and Heavy-tailed Claims

QIAO Ke-lin,ZHANG JUAN,LIU Qiong-qiong

(college of Mathematics and Computer Science,Yan′an University,Yan′an 716000,China)

2015-09-20

陕西省教育厅自然科学基金(2013JK0576)；陕西省高水平大学建设专项资金资助项目(2012SXTS07)；延安市科研计划项目(2014ZC-6)

乔克林(1964—)，男，陕西佳县人，延安大学副教授。

O211.9

A

1004-602X(2015)04-0008-05