非自治Cahn-Hilliard方程的拉回D-吸引子存在性

马腾洋，姜金平，雷思思

(延安大学数学与计算机科学学院，陕西延安716000)

非自治Cahn-Hilliard方程的拉回D-吸引子存在性

马腾洋，姜金平*，雷思思

(延安大学数学与计算机科学学院，陕西延安716000)

研究非自治Cahn-Hilliard方程的拉回D-吸引子的存在性。首先得到其存在拉回吸收集，然后借助拉回条件(C)，验证该类非自治Cahn-Hilliard方程的拉回D-吸引子的存在性。

非自治；Cahn-Hilliard方程；拉回D-吸引子

考虑如下的非自治Cahn-Hilliard方程：

ut+v△2u=△f(u)+g(x,t),

(x,t)∈Ω×(0,∞)，

(1)

u=△u=0，(x,t)∈∂Ω×(0,∞)，

(2)

u(x,τ)=uτ(x),t>τ。

(3)

式中：Ω是Rn(n≤3)的有界集，g(x,t)是依赖于时间t的外力项，是关于t的几乎周期函数。当

g(x,t)=0时是自治的Cahn-Hilliard方程。非线性项f(u)满足如下条件：

f′(u)>-k,F(u)>μ，

(4)

存在0<γ≤β≤∞使得

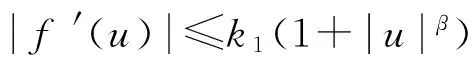
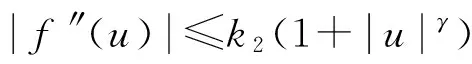
Cahn-Hilliard方程的解的存在性的研究已有大量工作[1-3]，文献[1，3]中，Cahn-Hilliard方程的全局吸引子得到广泛的研究。本文在文献[2]的基础上进一步研究其拉回吸引子的存在性。文献[4，5]研究的是非自治反应扩散方程的拉回吸引子的存在性。文献[6，7]从其它的方程等方面考察了拉回吸引子的存在性。本文采用文献[4]中的方法，证明了Cahn-Hilliard方程在空间L2(Ω)中拉回D-吸引子的存在性。

1 预备知识

令X是Banach空间，距离为d(·，·)，若一族定义于X上的双参数映射

U(t,τ):X→X,t≥τ,τ∈R满足：

1)U(t,τ)=U(t,r)U(r,τ),∀τ≤r≤t；

2)U(τ，τ)=Id,τ∈R。

则称U(t,τ)是一过程。

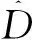
P(X)。

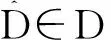
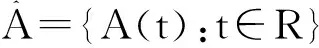
P(X)满足：

1)对任意的t∈R，A(t)是紧的；

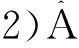
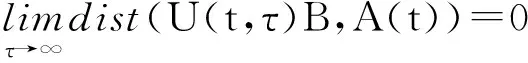
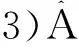
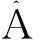
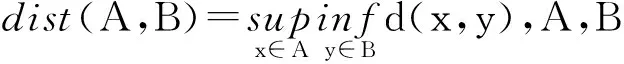
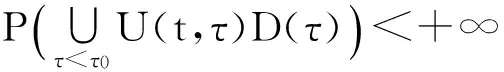
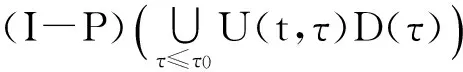
其中，P为X→X1的投影算子。

定理1[5]设X是一个Banach空间，U(t,τ)为X中的一个闭过程，且满足下列条件：

1)在X中存在一个拉回D-吸收集；

2)U(t,τ)满足拉回条件(C)；

那么在X中存在一个拉回D-吸引子

2 主要结论

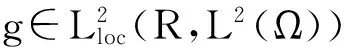
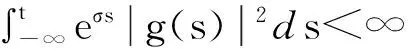
(6)

令D为L2(Ω)中的形如{D(t):t∈R}的所有非空子集，满足

(7)

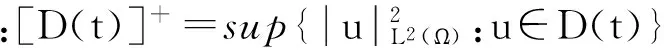
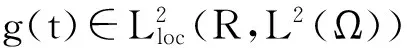
u∈C([τ,∞],H)∩ L2([τ,∞]，L2(Ω))。

该定理的证明是由Faedo-Galerkin方法得到的。具体证明见文献[1，5]。

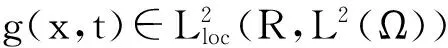
证明 对方程(1)两边用u做内积，有

=(△f(u),u)+(g(x,t),u)，

(8)

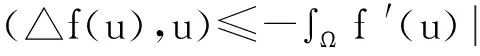
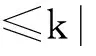
又由Young不等式和Holder不等式知

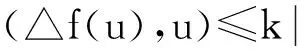
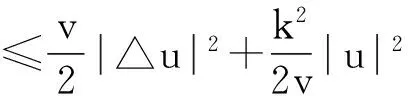
(9)

结合Poincare不等式，可得

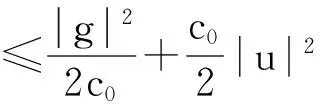
(10)

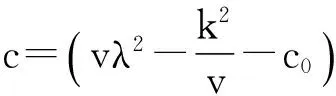
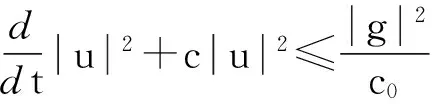
(11)

对(11)式运用Gronwall引理有

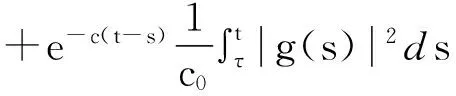
(12)

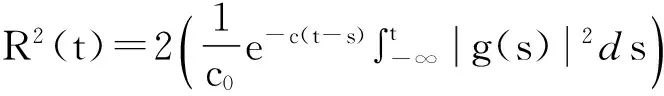
定理4 假设(2)-(5)成立，且满足(6)式，那么过程U在L2(Ω)中存在拉回D-吸引子。

证明 由定理3知，式(1)上的过程U在L2(Ω)中存在一个拉回D-吸收集。由定理1知只需满足拉回条件(C)即可。

令Vm=span{ω1，ω2，…，ωm}⊆V，Pm：V→Vm是一个正交投影算子。于是对于任意的u∈D(-△)，

记u=Pmu+(I-Pm)u=u1+u2。

对方程(1)同-△u2做内积，有

=(△f(u),-△u2)+(g(x,t),-△u2)。

(13)

因为 (△f(u),-△u2)=(▽f(u),▽△u2)≤ʃΩf ′(u)▽u2▽△u2dx≤c1ʃΩ▽u2▽△u2dx≤

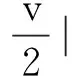
(14)

(15)

将(14)、(15)代入(13)式，整理得

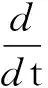
(16)

运用Poincare不等式，可得

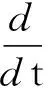
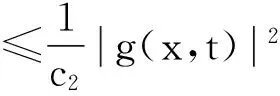
(17)

对(17)式，由Gronwall引理可知

‖u2(t)‖2≤‖u2(τ)‖2e-λm+1(t-τ)+

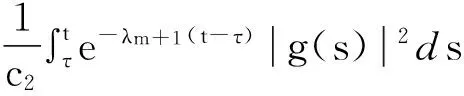
(18)

下面对(18)式中右侧的每一项进行估计。

对于第1项，当m+1充分大时，有

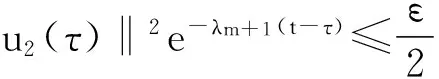
(19)

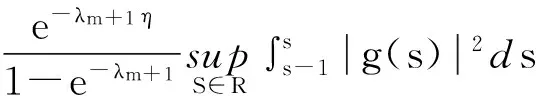
(20)

对于上式，当η足够小且λm+1充分大时，有

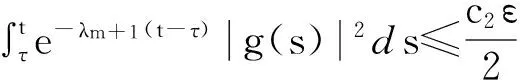
(21)

由(19)、(21)式可得

‖u2(t)‖2≤ε。

因此结论成立，证毕。

[1]TemanR.Infinite-dimensionaldynamicalsystemsinmechanicsandphysics[M].NewYork:Springer,1997.

[2]董超雨，姜金平，张晓明.非自治Cahn-Hilliard方程的一致吸引子[J].郑州大学学报(理学版)，2014，46(2)：21-23，30.

[3]王素云，李德生，张艳红.Cahn-Hilliard方程强解的全局吸引子[J].兰州大学学报(自然科学版)，2005，41(5)：134-137.

[4]任丽，李晓军.非自治反应扩散方程的拉回D-吸引子[J].江南大学学报，2014，13(2)：237-242.

[5]SongHaitao,WuHongqing.Pullbackattractorsofnonautonomousreaction-diffusionequations[J].JournalofMathematicalAnalysisandApplications, 2007,325(2):1200-1215.

[6]Marn-RubioP,RealJ.Ontherelationbetweentwodifferentconceptsofpullbackattractorsfornon-autonomousdynamicalsystems[J].NonlinearAnalysis,2009,71(9):3956- 3963.

[7]Garca-LuengoJ,Marn-RubioP,RealJ.PullbackattractorsinVfornon-autonomous2D-Navier-Stokesequationsandtheirtemperedbehaviour[J].JournalofDifferentialEquations,2012,252(8):4333-4356.

[责任编辑 毕 伟]

Existence of PullbackD-Attractors for Non-autonomous Cahn-Hilliard Equation

MA Teng-yang,JIANG Jin-ping*,LEI Si-si

(College of Mathematics and Computer Science,Yan′an University,Yan′an 716000,China)

The existence of pullbackD-attractor of the non-autonomous Cahn-Hilliard equation was investigated.Firstly,the existence of pullback absorbing set was given,then it was proved the existence of pullbackD-attractors for the class of the non- autonomous Cahn-Hilliard equation by the pullbackD- condition(C) .

non- autonomous; Cahn-Hilliard Equation; pullbackD-attractors

10.13876/J.cnki.ydnse.2015.04.001

2015-09-29

国家自然科学基金项目(11171269)；陕西省自然科学基础研究计划项目(2014JM2-1005)

马腾洋(1991—)，男，陕西洋县人，延安大学硕士研究生。 *为通讯作者

O175.29

A

1004-602X(2015)04-0001-03