重尾索赔下保费收入随机化风险模型的破产概率

乔克林，刘琼琼，张 娟

(延安大学数学与计算机科学学院，陕西延安716000)

重尾索赔下保费收入随机化风险模型的破产概率

乔克林，刘琼琼，张 娟

(延安大学数学与计算机科学学院，陕西延安716000)

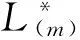
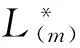
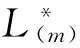
本文首先在文献[4-7]的基础上，建立同时考虑利率、保费收取随机化且索赔属于S族的风险模型，在模型中假定索赔计数过程为Poisson过程和保费到达过程为一般更新过程，借助概率论知识、随机过程及文献[6，7]中的方法，得出了该模型在t时刻盈余为负的概率渐近等价式。

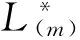
1 模型的建立

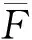
(1)设Xi为第i张保单的保费额，{Xi,i≥1}是一列独立同分布的非负随机变量序列，其具有共同的分布函数F1和有限的数学期望μ1>0；

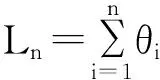
E[N1(t)]是更新函数；

(3)Yj为第j次的索赔额，{Yj,j≥1}是一列独立同分布的非负随机变量序列，其具有共同的分布函数F2和有限的数学期望μ2>0；

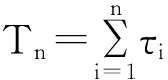
mN2(t)=E[N2(t)]=λt；

(5){Xi,i≥1}，{Yj,j≥1}，{N1(t),t≥0}与

{N2(t),t≥0}相互独立。

建立常利率更新风险模型为：

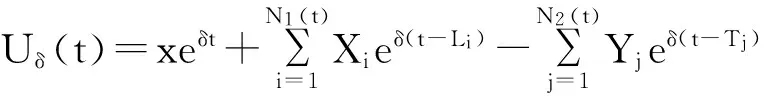
(1.1)

现建立模型(1.1)的贴现过程：

(1.2)

其中δ≥0为常利率。

对于上述风险模型(1.2)，我们定义在任意给定t>0时刻盈余为负的概率为

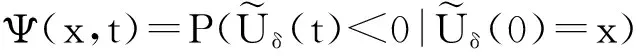
2 重尾分布与重要引理

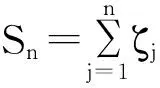
本文研究索赔分布为重尾的情形，下面给出几个与本文有关的重尾子族(详情可参见[3，8，9])，其中分布F以[0,∞)为支撑集。

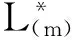
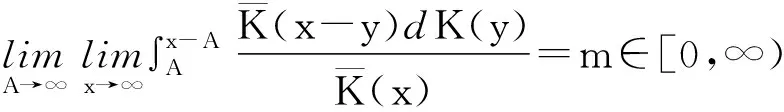
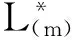
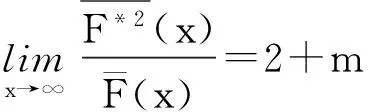
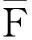
介绍了一些重要的子族后，现给出相关的重要引理。

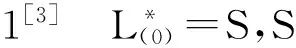
(U(1)，U(2)，…U(n))。

引理3[6]设X和Y是独立非负随机变量，如果X的分布F∈S，而Y有界且非退化到0，那么乘积XY的分布H∈S。

引理4[6]设分布W∈S，则对任意ε>0，存在一个C=C(ε)>0，使得

对所有n∈N和一切x≥0都成立。

引理5[9]设ζj，j=1，2，…为独立随机变量序列，具有分布Kj∈L，则对任意的n≥1，有

由引理5可得下面结果：

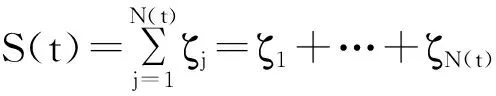
其中N(t)是从0时刻开始计数的计数过程。

证明 由引理5及全概率公式可得

即证。

注：当m=0时，可得到如下结果(参见[8]中的lemmaA3.15)：

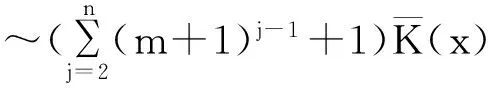
注：(1)令m=0时，可得下面已知结果：

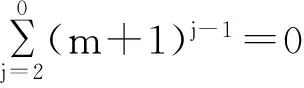
3 主要结果

下面给出本文的主要结果：

定理3.1 在模型(1.2)中，索赔量{Yj,j≥1}为独立同分布的非负随机变量序列，其分布函数F2∈S，则在t时刻盈余为负的概率可渐近表示为：

(3.1)

证明：风险模型(1.2)：

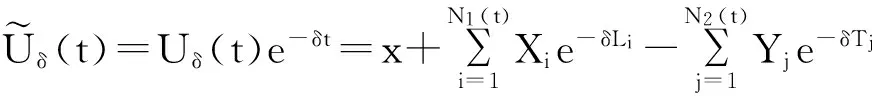
P(N2(t)=r)

P(N1(t)=n)P(N2(t)=r)

P(N1(t)=n)P(N2(t)=r)

P(N1(t)=n)P(N2(t)=r)

P(N1(t)=n)P(N2(t)=r)。

由假定条件及引理3可知，Yje-δUj是独立同分布的，记其分布为F且F∈S。

根据引理4，对任一固定ε>0，存在常数C=C(ε)>0，有下面不等式成立。

dFL1…Ln(t1,…,tn)P(N1(t)=n)

P(N2(t)=r)

(3.2)

dFL1…Ln(t1,…,tn)P(N1(t)=n)P(N2(t)=r)

=r)dF1(x1)…dF1(xn)dFL1…Ln(t1,…,tn)

P(N1(t)=n)

dFL1…Ln(t1,…,tn)P(N1(t)=n)

E(e-τ)]retP(N2(t)=r)dF1(x1)…dFn(xn)

dFL1…Ln(t1,…,tn)P(N1(t)=n)，

其中τ表示分布为G的代表性的随机变量。

则存在ε>0，使得(1+ε)E[e-τ]<1。于是，存在常数η0>0，一致地有

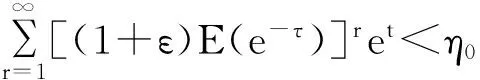
所以

dFL1…Ln(t1,…,tn)P(N2(t)=n)≤Cη0<∞。

dF1(x1)…dF1(xn)dFL1…Ln(t1,…,tn)

P(N1(t)=n)P(N2(t)=r)

dF1(x1)…dF1(xn)dFL1…Ln(t1,…,tn)

P(N1(t)=n)=mN2(t)=λt。

所以

Ψ(x,t)～λtP(Yje-δUj>x)=

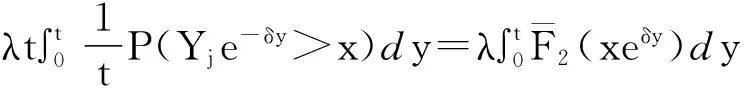
即证(3.1)式成立。

在模型(1.1)中，当常利率δ=0时，模型(1.1)变形为

(3.3)

将风险过程定义为

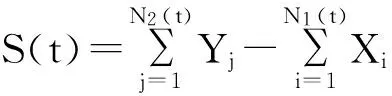
(3.4)

由于破产仅发生在索赔到达的时刻，显然有

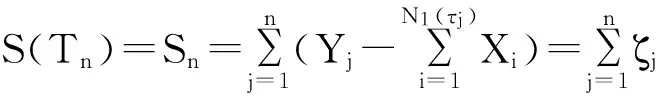
现进一步假定相对安全负荷条件满足

所以

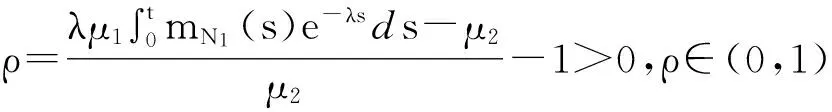
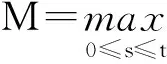
φ(x,t)=P(U(s)<0,∃0≤s≤t|U(0)=x)

在风险模型(3.4)中，当F2∈L*(m)时，得到下面结论。

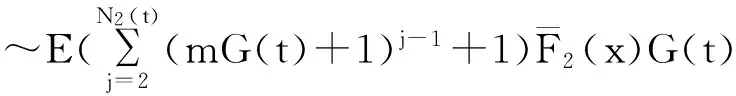
其中G(t)=1-e-λt。

dG(s)。

P(N1(s)=r)dG(s)

P(N1(s)=m)dG(s)

=G(t)∈(0,∞)，(对给定的t>0)。

故有

(3.5)

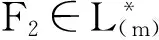
(3.6)

由于破产仅发生在索赔到达的时刻，且K⊂L，故由引理6及全概率公式，可知对x≥0有

φ(x,t)=P(U(s)<0,∃0≤s≤t|U(0)=x)

再根据(3.6)式及定理1知对任意的ε>0，有

故根据定理1和控制收敛定理得

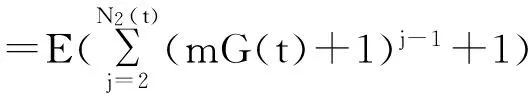
结合(3.5)式，有

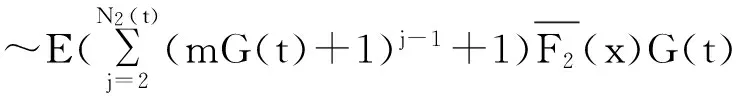
在定理3.2中令m=0，得如下结论。

推论3.1 在上述更新风险模型(3.4)中，设F2∈S，且mN2(t)=λt<∞，则在有限时间(0,t]内的破产概率可渐近表示为

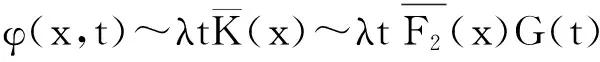
证明：利用类似于定理3.2的方法即可证。

4 结束语

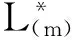
[1]包振华，叶中行.重尾索赔下双复合Poisson风险模型的赤字尾分布[J].汕头大学学报，2008，25(1)：10-14.

[2]马树建，王晓谦.重尾分布情况下一类破产概率的研究[J].南京工业大学学报，2007，29(1)：97-99.

[3]黄宝安，尹传村.一类重尾分布下的随机游动的渐近结果及其在风险理论中的应用[J].应用数学学报，2009，32(1)：28-36.

[4]何莉娜，刘再明.保费收取为随机过程且带常利率的破产模型[J].吉首大学学报(自然科学版)，2006，27(2)：9-11.

[5]陈珊，莫晓云.带常利率的双Poisson模型的破产概率[J].经济数学，2006，23(4)：331—341.

[6]肖鸿民，李红.重尾赔付下带常数利息力的延迟索赔风险模型的破产概率[J].西北师范大学学报(自然科学版)，2011，47(6)：17-19.

[7]吴永，邵明阳.重尾索赔下常利力更新风险模型的破产概率[J].重庆理工大学学报(自然科学)，2010，24(10)：97-100.

[8]EmbrechtsP,KlüppelbergC,MikoschT.ModellingExtremalEventsforInsuranceandFinance[M].Berlin：Springe-Vrerlag,1997.

[9]NgKW,TangQ,YangH.MaximaofSumsofHeavy-tailedRandomVariables[J].AstinBulletin,2002,32(1):43-55.

[10]刘莉，茆诗松.常利率下风险模型破产问题的研究[D].上海：华东师范大学数学系，2004.

[责任编辑 毕 伟]

Ruin Probability of Risk Model with Stochastic Premium under Heavy-tailed Claims

QIAO Ke-lin,LIU Qiong-qiong,ZHANG JUAN

(College of Mathematics and Computer Science,Yan′an University,Yan′an 716000,China)

2015-09-28

陕西省教育厅自然科学基金(2013JK0576)；陕西省高水平大学建设专项资金资助项目(2012SXTS07)；延安市科研计划项目(2014ZC-6)

乔克林(1964—)，男，陕西佳县人，延安大学副教授。

O211.9

A

1004-602X(2015)04-0013-05