圆柱正弦活齿传动机构传动比和传动条件研究*
2015-06-14曾运运袁新梅周思柱
□ 曾运运 □ 袁新梅 □ 周思柱
长江大学机械结构强度与振动研究所 湖北 荆州 434000
活齿传动分为平面活齿传动和空间活齿传动,目前为止,活齿传动研究主要集中在平面活齿,而空间活齿传动研究得比较少,但现在已经有学者开始将平面活齿传动理论和空间活齿传动理论联系起来进行研究。文献[1]分析了圆柱面空间活齿传动和平面活齿传动,指出可以将圆柱面活齿传动转化为平面活齿传动来分析。圆柱正弦活齿传动属于圆柱面空间活齿传动,笔者采用展开法,将圆柱正弦活齿传动转化为平面活齿传动,推导出该传动的传动比公式和连续传动条件,并进行实例计算,验证上述结论。
1 传动比计算
圆柱正弦活齿传动主要由主动轴、壳体、导架及活齿4个部分组成,主动轴外表面有外正弦滚道,周期数为Z1,活齿架上均匀分布着轴向活齿槽,壳体内表面有内正弦滚道,周期数为Z3,在外、内滚道及活齿槽交错区域内安装球形活齿。
为了便于分析,将壳体固定,以主动轴为输入轴,活齿架为输出轴,推导传动比公式。转角φ0和角速度ω之间的关系为ω=因此,主动轴和活齿架之间的传动比可以用转角来表示。该传动机构在工作过程中,活齿沿外正弦滚道作相对运动,沿内正弦滚道作绝对运动,图1为活齿沿外、内正弦滚道运动平面的展开图,线1和线2分别代表外、内正弦滚道的正弦轨迹,θ0代表活齿初始位置。线3代表线1在主动轴旋转Δθ后的曲线,线1、2、3的方程如下:

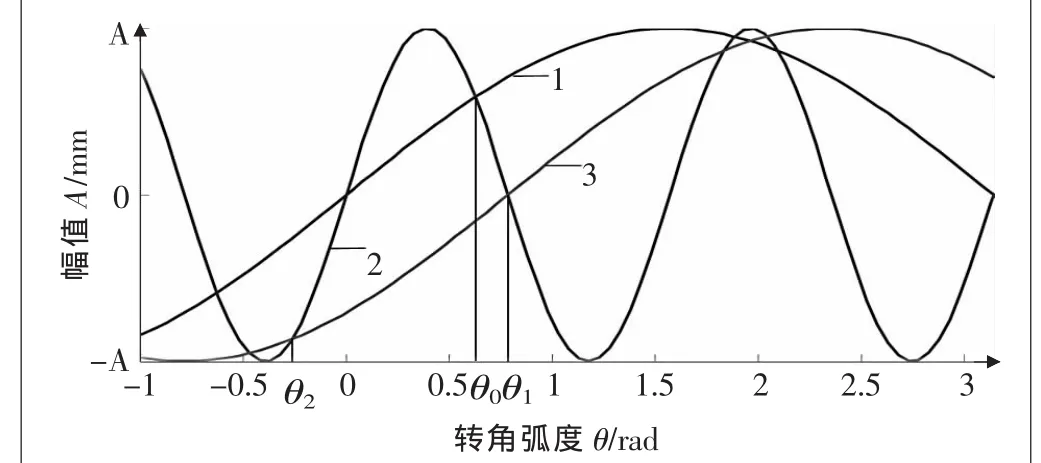
▲图1 活齿轨迹平面展开图
当活齿在初始位置 θ0时,联立式(1)和式(2)可得:
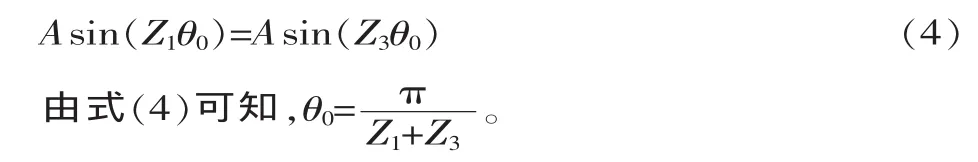
若主动轴和活齿架同向运动,当主动轴转过角度为Δθ1、活齿由初始位置θ0转到θ1时,其转过角度为Δθ2,联立式(2)和式(3)可得:

若主动轴和活齿架反向运动,当主动轴转过角度为Δθ1,活齿由初始位置θ0转到θ2时,其转过角度为Δθ2。 联立式(2)和式(3)可得:
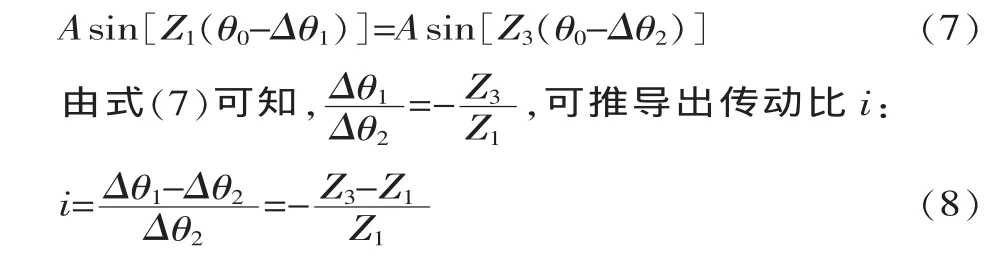
2 连续传动条件
连续运动条件是圆柱正弦活齿传动机构正常工作所必须满足的条件之一[2]。圆柱正弦活齿传动机构连续传动条件为:在工作中至少有一个活齿处于啮合状态,并且所有活齿均可连续接触正弦滚道齿面。
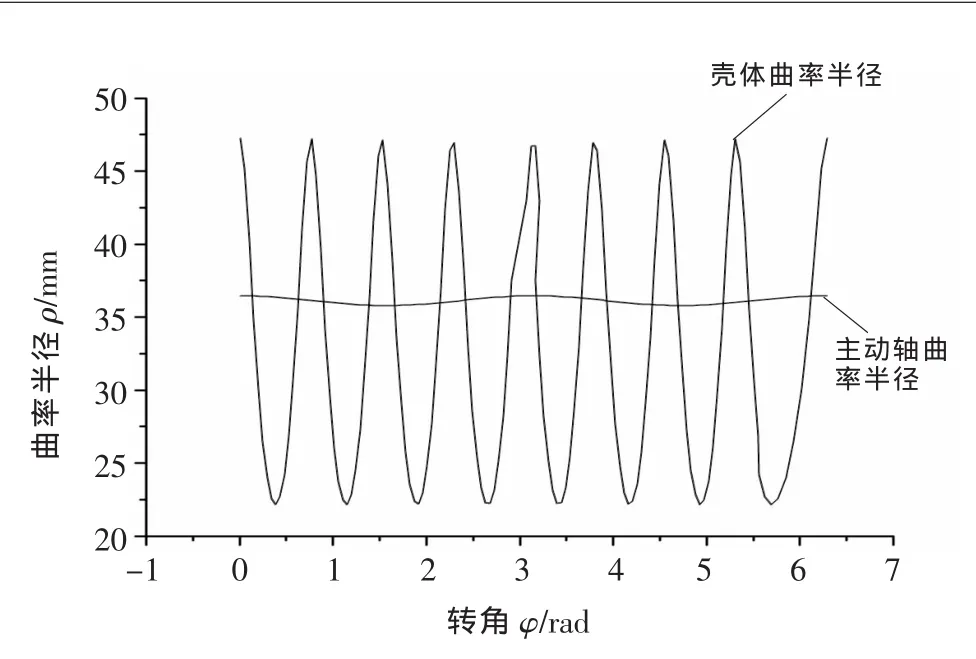
现以活齿在主动轴外正弦滚道运动为例,将主动轴外圆表面沿直母线展开。由外正弦滚道形状得知,当活齿啮合区域的小圆半径ra小于主动轴外正弦滚道理论齿廓曲线L的最小曲率半径ρmin,即ρmin>ra时,则不会发生顶切;当ρmin 式中:r1为主动轴半径;φ为活齿中心在圆周方向的位置角;A为正弦幅值。 曲线L上任意一点的位置矢量r=xi+yj+zk,根据微分几何[3]可知曲率 ρ: 将式(9)代入式(10)中,求解得到主动轴最小曲率半径为: 当ρmin>ra时,主动轴的外正弦滚道理论齿廓曲线不会发生顶切。根据活齿结构的几何关系有ra= 式中:b1为主动轴的正弦滚道深度;r0为活齿半径。 同理,可得壳体正弦滚道理论齿廓曲线最小曲率半径为: 从而得出壳体正弦滚道理论齿廓曲线不发生顶切的条件为: 式中:b3为壳体的正弦滚道深度;r3为壳体的内圆柱面半径。 已知圆柱正弦活齿传动机构的初始参数为Z1=1、Z3=4、A=4mm及主动轴和活齿架同向转动,利用式(6)可知,圆柱正弦活齿传动机构的传动比i=5。 为保证滚道齿面不发生顶切,要求各结构参数满足式(12)、式(14),以此来确定该传动机构的结构参数,见表1。 表1 圆柱正弦活齿传动结构参数 ▲图2 主动轴曲率半径变化曲线 利用式(11)、式(13)可以算出主动轴滚道理论正弦齿廓曲线最小曲率半径ρmin=35.78mm和壳体滚道理论正弦齿廓曲线最小曲率半径ρmin=22.12mm,利用Pro/E曲率分析功能,对主动轴和壳体理论正弦齿廓曲线进行分析,绘制曲率半径随相对角度变化的曲线,如图2所示。通过分析发现,由Pro/E计算的主动轴和壳体的最小曲率半径与由式(11)、式(13)算出的主动轴滚道和壳体滚道的理论正弦齿廓曲线最小曲率半径完全吻合,可以证明式(11)、式(13)完全正确。将上述结构参数代入 ra=中,可求出ra=3.69mm,最小曲率半径远远大于ra,所以,活齿可以在主动轴和壳体的正弦滚道中连续运动,不会发生顶切。 (1)圆柱正弦活齿传动机构的传动比主要由主动轴正弦滚道周期数Z1、壳体正弦滚道周期数Z3和主动轴与活齿架转向决定。 (2) 所选结构参数必须满足式(12)、式(14),才能保证圆柱正弦活齿传动机构能够连续运动。 [1] 黄劲枝,陈贤湘,程时甘.双余弦活齿传动啮合曲线的研究[J].机械传动,2008(4):6-7. [2] 曲继方.活齿传动理论[M].北京:机械工业出版社,1993. [3] 傅则绍.微分几何与齿轮啮合原理[M].青岛:石油大学出版社,1999.




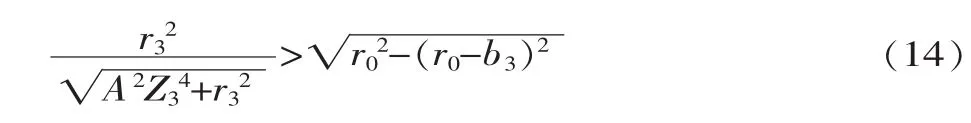
3 计算实例

4 结论
