转动热力学系统热力学性质研究

潘营利

(渭南师范学院 数理学院，陕西渭南714099)

在热力学统计物理［1－3］教材中，人们大多研究的是相对于惯性系处于静止状态的热力学系统，给出了该热力学系统的热力学关系、热力学函数及热力学平衡条件，对于相对于惯性系运动的热力学系统则没有讨论，对于相对于惯性系做转动的热力学系统则从来没有讨论过.王风［4］研究了谐振子势阱中理想费米气体的化学势，李玉山［5］利用数值方法研究了谐振子势阱和磁场中的带电荷玻色气体;李永平［6］研究了圆柱形离心机中的理想气体的热力学性质，但仅给出了系统的热力学函数，且有些结果存在问题.本文将以处于半径为R，高为h的圆柱体中的单原子理想气体作为热力学系统，从经典统计出发，对系统作匀角速转动时的热力学问题进行详细讨论，给出了该系统的描述方法、热力学函数及热平衡条件，从而使人们对转动热力学系统有一个简单的了解.

1 转动热力学系统的描述方法

对于转动热力学系统，教科书上给出的关于静止热力学系统的热力学函数和热力学关系将无法使用，那么对于转动热力学系统应该如何描述呢?我们首先解决这个问题.

对于一个体积为V的转动圆柱体中的单原子理想气体系统，设分子总数为N，温度为T，要求得系统的热力学量，先要求出其转动情况下的配分函数

其中:i是态标.从Z的表达式可以看出，要计算Z需要知道两个信息:一是一个粒子的能量是状态的什么样的函数，另一个是一个粒子可取什么样的状态(可及态).因为表示对所有可能状态求和，这两个信息取决于宏观系统的微观模型(所以统计物理对宏观热力学系统首先要提出一个合理的微观模型假设)，根据这个微观模型，从力学知识可获得计算Z所需要的两个信息.现在对单原子理想气体提出的微观模型是:把分子看成一个无内部结构的质量为m的质点，根据经典力学，这个具有3个平动自由度的质点的能量与状态的关系，若取直角坐标系，则有:.其中:p为粒子的动量，up为由于系统的转动使每个分子所具有的势能，由文献［7］知，其值为:

2 转动热力学系统的热力学函数

2.1 粒子的配分函数Z［1］

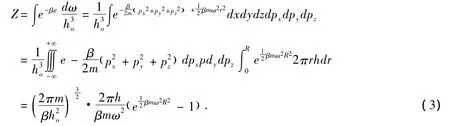
2.2 转动热力学系统的内能

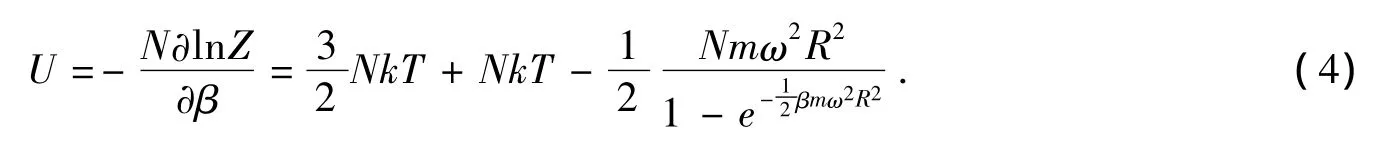
其中:第一项为在没有转动情况下理想气体的内能，而其余项就是由于转动所产生的附加能量.

下面推导转动热力学系统的压强和粒子数密度的分布.

如图1所示，取一薄圆柱壳，半径由r→r+dr，由于转动时薄圆柱壳内的气体需要向心力，它由薄圆柱壳外表面和内表面的压力差来提供.故有:

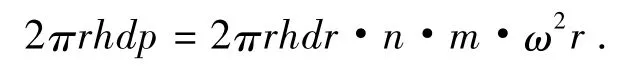
其中:n为r处的分子数密度，dp=mω2nrdr.

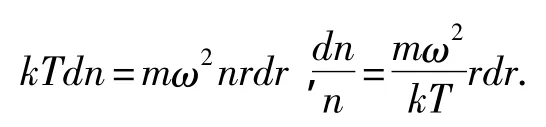
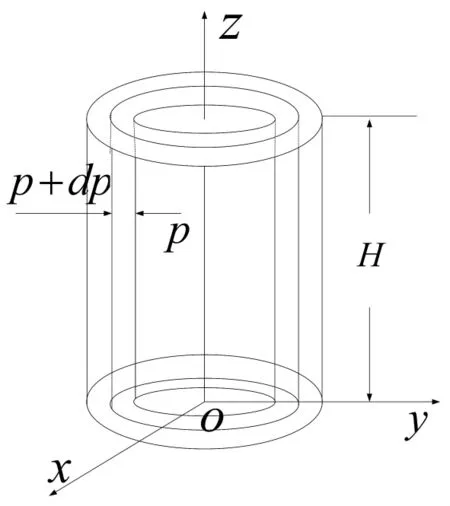
图1 推导转动热力学系统压强用图

其中:p0=n0kT.

对于n0可用归一化条件来确定:

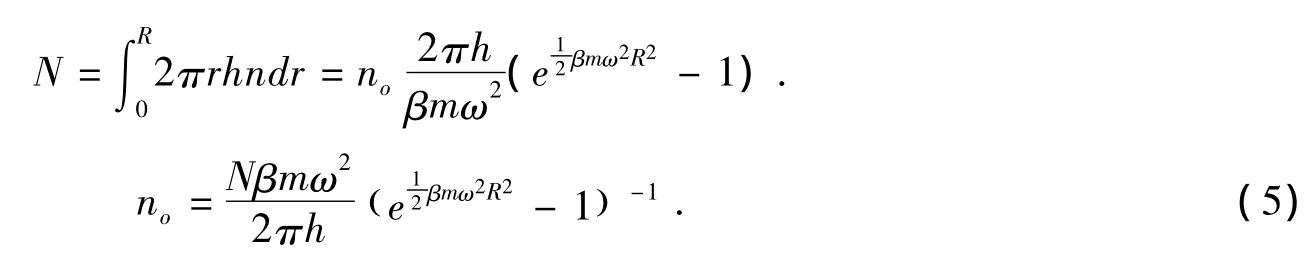
可以看到圆柱体在匀速转动的情况下压强的分布是不均匀的，而且随着粒子离轴心的垂直距离的变化而变化，离轴心越远压强越大，同样粒子数密度也是随半径的增大而增大.

气体的定容热容量为:

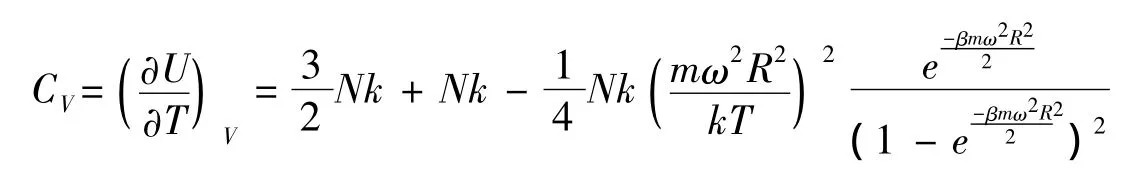
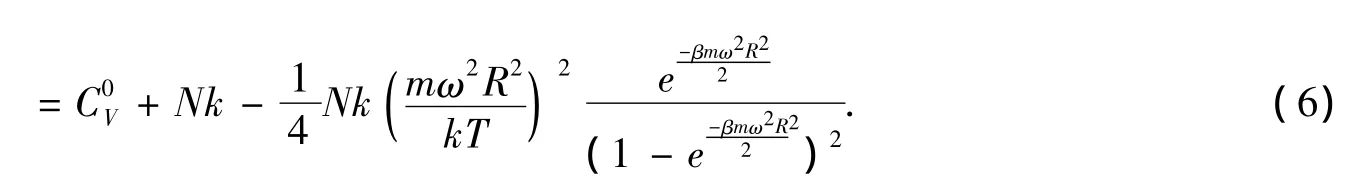
2.3 转动热力学系统的熵

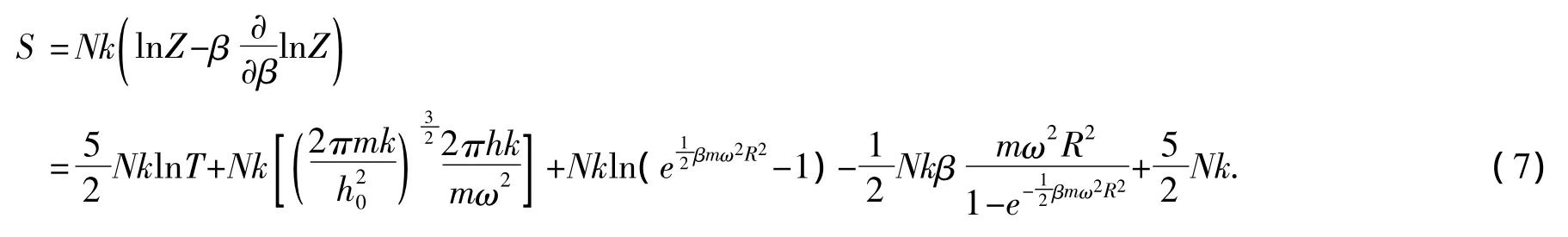
3 转动热力学系统的平衡条件

转动热力学系统中的气体分子即使处于平衡态时，气体分子内部各处的性质也不是完全相同的.因此把气体分为许多小的部分，把每一小部分作为处于平衡态的均匀系.设这一小部分的质量为DM，内能为DU，熵为DS，体积为DV，所含分子数为DN，则根据热力学第二定律有

其中:T为温度，p为压强，μ为粒子化学势，这些都与所考虑的小部分的地点有关.设φ(x，y，z)为单位质量在转动热力学系统中的势能，φDM为所考虑的小部分气体的势能，x，y，z是这一小部分的坐标.这一小部分的总能量DE将是(不计动能)

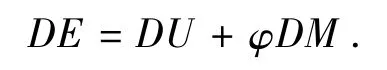
对气体分子体所占据的全部空间求积分，得气体的总能量E为

那么，在气体分子达到平衡态时，各处的温度、压强和化学势将满足什么关系呢?也就是说，对转动热力学系统其平衡条件是什么?为了解决这个问题，我们将运用热动平衡条件中的最后一个平衡判据，就是能量判据［3］，即在总熵和几何位形不变的情形下，平衡态的总能量最小.引入拉格朗日待定乘子τ和λ，得

由(9)式得

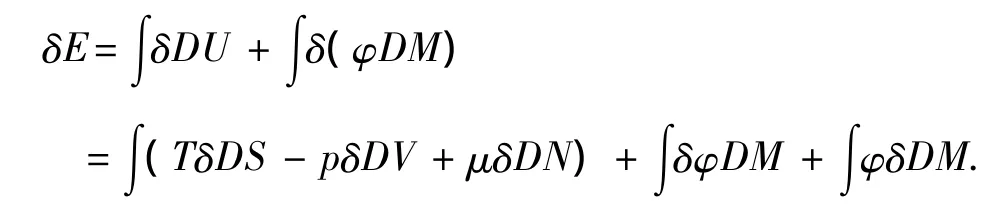
代入(10)式得

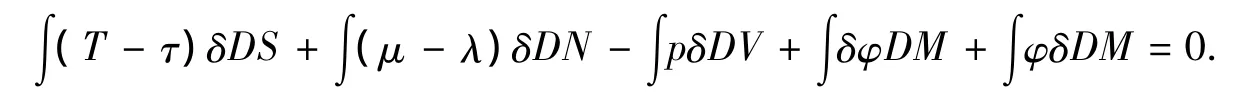
设m为分子的质量，则DM=mDN，而上式化为

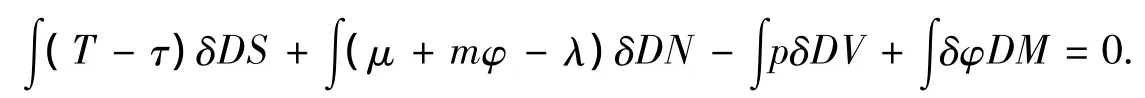
由此得到平衡条件为

其中:(11)式是热平衡条件，指明温度是到处一样的，这与没有转动时的情形相同.(12)式是相平衡条件，这个条件受转动的影响，(12)式也可写为

(13)式是力学平衡条件，根据力学定律可以证明［3］，(13)式还可写为

4 结论

(1)通过计算给出了转动热力学系统的各个热力学函数，结果表明:各个热力学函数均受到转动的影响，转动角速度ω越大，与无转动时的热力学函数的差别越大.

(2)转动热力学系统即使处于平衡状态，粒子数密度和压强的分布也是不均匀的，r越大，粒子数密度和压强越大.

(3)对于转动热力学系统，其热平衡条件不受转动的影响，而力学平衡条件和相平衡条件则受转动的影响，出现修正项.

［1］汪志诚.热力学统计物理［M］.第4版.北京:高等教育出版社，2008.

［2］熊吟涛.热力学［M］.北京:人民教育出版社，1979.95－111.

［3］王竹溪.热力学［M］.第2 版.北京:高等教育出版社，1957.201－203.

［4］王风.谐振子势阱中理想费米气体化学势研究［J］.湖北理工学院学报，2013，(6):59－62.

［5］李玉山.数值方法研究谐振子势阱和磁场中的带电荷玻色气体［J］.原子与分子物理学报，2014，(5):821－825.

［6］李永平.圆柱形离心机中的理想气体的热力学性质［J］.廊坊师范学院学报(自然科学版)，2009，(1):55－57.

［7］［苏］朗道，E.M.栗佛席兹.热力学·统计物理［M］.北京:人民教育出版社，1956.92－94.