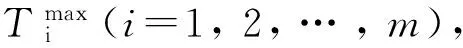探讨无标度网络(图)的平衡集*
2015-06-13姚东任张婉佳
刘 霞,姚东任,姚 兵,张婉佳
(1.西北师范大学数学与统计学院, 甘肃 兰州 730070; 2.西北师范大学计算机科学与工程学院,甘肃 兰州 730070)
探讨无标度网络(图)的平衡集*
刘 霞1,姚东任2,姚 兵1,张婉佳1
(1.西北师范大学数学与统计学院, 甘肃 兰州 730070; 2.西北师范大学计算机科学与工程学院,甘肃 兰州 730070)
无标度网络的无标度性导致其各顶点之间的连接状况(度数)具有严重的不均匀分布性, 无法给出无标度网络的具体结构,不能直接观察信息传播的具体路径。基于利用生成树来研究无标度网络(图)的拓扑结构思想,尝试寻找与时间和次要节点无关的无标度网络(图)的普适性结构, 研究与生成树密切相关的平衡集,给出一个寻找具有较多叶子生成树的算法。
平衡集;连通图;生成树;无标度网络
现实中的许多网络都带有无标度特性,例如因特网,金融系统网络,通信网络 (万维网和互联网),社交网络(研究合作作者,电影演员),生物网络(神经网络,代谢网络,蛋白质网络,生态和食品网),电话图表,邮件网络,电网和电子电路,软件组件的网络,以及能源景观网络等等。具有无标度性的网络叫做无标度网络。已知大数据在执法、经济规划、防灾和灾后恢复等方面已有应用。一些国家将“大数据战略”上升为最高国策,认为大数据是“未来的新石油”,可以“挖出商业金矿”,将对数据的占有和控制作为陆权、海权、空权之外的另一种国家核心能力。无标度网络的无标度性是描述大量复杂系统整体上严重不均匀分布的一种内在性质,其典型特征是在网络中的大部分顶点只和很少节点连接,极少数Hub节点与非常多的节点连接。这种严重的异质性,导致其各顶点之间的连接状况 (度数) 具有严重的不均匀分布性,少数Hub节点对无标度网络的运行起着主导的作用。但是,“无标度网络的具体结构无法给出。作为信息存储的重要载体,节点通过链接实现信息交互,然而,节点的信息来源通常难以确定,信息传播的具体路径不能直接观察[1]。”探讨无标度网络的拓扑结构成为当务之急。
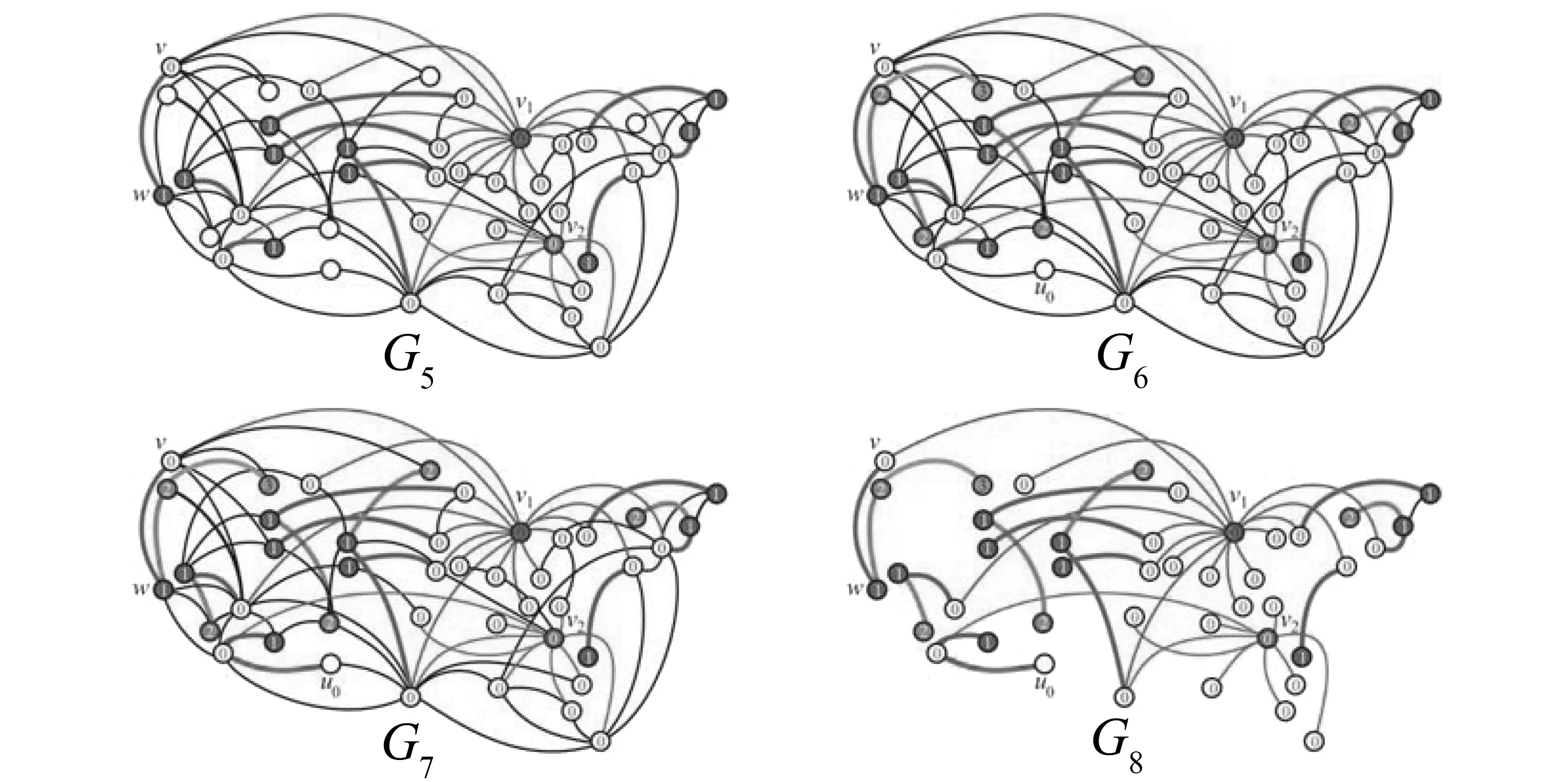
众所周知,图论中的生成树已经成功地应用到实际问题,积累了丰富的理论[2-4]。最典型的应用之一是 Radia Perlman[5]利用生成树与网络间的结构关系发明了广泛用于网桥、交换机上生成树协议。已有大量运用生成树的算法,例如最小生成树对电网的优化;以及物流运输费用在货物配送过程中对配送区域的划分与配送路线的优化选择等。本文利用生成树来研究无标度网络 (图) 的拓扑结构,尝试寻找与时间和次要节点无关的无标度网络 (图) 的普适性结构[6-8]。研究与生成树密切相关的平衡集是本研究的一个关键。称有p个顶点和q条边的图G为(p,q)-图,nd(G)是G中度数为d的顶点数目。文中论及的图均为简单、无向、有限图,并采用标准的图论术语和符号。记号[m,n]表示集合{m,m+1,m+2,…,n},其中m和n均为整数, 且满足0 定义1[8]集合X是连通图G的平衡集,如果它满足 (1) 为研究的需要,我们给出如下的几个概念。 设连通图G的全体具有最多叶子的生成树为T1max,T2max, …,Ttmax,令 引理1[9]每个连通(p,q)-图G满足 (2) 引理2[6]设G是连通(p,q)-图,D(G)是图G的直径。 (i)G有一棵叶子最少的生成树T,使得D(T)=D(G),且T包含G的一条最长路。 (ii)G包含一棵叶子最多的生成树Tmax,使得Δ(G)=Δ(Tmax),n1(Tmax)≤p-D(G)+1。 命题1 每个连通(p,q)-图G含有一棵生成树Tmax,使得 2+[Δ(G)-2]nΔ(G)≤n1(Tmax)≤p-D(G)+1 (3) 证明 若连通(p,q)-图G是一棵树,引理得证。当G不是一棵树,则有如下的算法: 输入:连通 (p,q)-图G。 输出:图G的一棵生成树T。 ① 打断图G的自环,记余图为H0; ② 删去Hi中一个圈上的一条边uivi,Hi+1←Hi-uivi,i←i+1; ④ 返回生成树T。 首先,上述算法的正确性是显然的。这是因为图G的边数目是有限的,且每次只删去一个圈上的一条边;其次,生成树Tmax的存在性是显然的。 2+[Δ(G)-2]nΔ(G)(G) 因为n1(T)≤n1(Tmax),再根据引理2中的结论(i),可推出得不等式(3)中的上界。 命题2 若连通图G的最小平衡集为S,则它的任何连通支撑子图的最小平衡集亦为S。 证明 因为连通图G的连通子图的生成树也是G的生成树,由平衡集的定义,本命题得证。 命题3 若连通图有一个割点,则它的每一个平衡集包含此割点。 证明 设u为连通图G的一个割点。因为G的任何生成树包含割点u,且割点u不是任何生成树的叶子, 本命题得证。 命题4 设连通图G的所有叶子的集合记为L(G),则G有一个平衡集S=V(G)L(G)。 证明 令L(G)=L。若L=Ø,显然结论成立,下证L≠Ø,结论成立。如果L≠Ø,则由生成树的定义可知,对G的生成树T,有L⊆L(T),如若不然,至少存在一个顶点u0∈L,而u0∉L(T),即u0为T中非叶子顶点,这导致u0为G中非叶子顶点,矛盾!下证S=V(G)L(G)为平衡集。 由定义2,对图G的任意2棵生成树T和H,有 同理, 说明生成树T和H满足(1)式,即S为连通图G的平衡集。 定理1 若连通图G含有 Hamilton圈,则它的平衡集只有V(G)。 ① 若L∩≠Ø,那么L∩及其所有子集为图G的TM-平衡集。 结论 (1) 成立。 结论 (2) 成立。 所以,X∪S为图G的一个TM-平衡集。定理得证。 我们会发现,在一个无标度网络N(t)中,当t很大时,N(t)的TM-平衡集必然满足L∪⊆V(G),L∩≠Ø。也就是说对N(t)的任意TM-生成树,总有某些点是非叶子节点,而只是这些点构成了网络N(t)的骨架,同样,总有某些点是叶子节点,而且叶子节点数远大于非叶子节点数。 例1 完全图不含真平衡集,也不含TM-平衡集,且它的任意2棵具有最多叶子的生成树同构。 证明 设图Kn是n个顶点的完全图,则易知Kn包含Cn子图,故不含有真平衡集。我们给出另外一种证明方法。设Kn的顶点集为{a1,a2, …,an},可知Kn的生成树叶子最多为n-1个,且对任意的Tjmax,有L(Tjmax)=V(Kn){ai}(i∈[1,n]),计算TM-平衡交集和TM-平衡并集,得 ∩L(Tjmax)=∩(V(Kn){ai})= V(Kn)(∪{ai})=Ø; ∪L(Tjmax)=∪(V(Kn){ai})= V(Kn)(∩{ai})=V(Kn) 根据定理2,完全图Kn无TM-平衡集。由于完全图Kn的具有最多叶子的生成树是星K1, n-1,所以它的任意2棵具有最多叶子的生成树同构。 例2 完全二部图Km,n不含真平衡集和TM-平衡集,且它的任意2棵具有最多叶子的生成树同构。 ∩ijL(Tij)=∩ij(V(Km,n){u,,vj})= V(Km,n)∩ij{ui,vj}=Ø 和∪ijL(Tij)=∪ij(V(Km,n){ui,vj})=V(Km, n)。根据定理2,完全二部图Km,n不含TM-平衡集,也没有真平衡集。前面已经给出完全二部图Km,n的具有最多叶子的生成树均为双星,也就是说,Km, n的任意2棵具有最多叶子的生成树同构。 要寻找网络N(t)的真平衡集及TM-平衡集,我们就必须先找到它的生成树,针对CDSP (connecteddominating set problem)和MLATP (maximum leaf spanning tree problem)问题,文献[10]的作者用分治技术(measure-and-conquer technique)给出寻找n个节点网络生成树Tmax的时间为O(1.896 6n)的一个精确算法。然而,寻找生成树Tmax是NP困难问题[11]。Barabsi和Bonabeau[12]发现,少数高连通网页将整个WWW支撑连接在一起,其中80%的网页平均只有4个连接,占总网页数目0.01的网页每个却有不小于1 000个的连接。依据这个事实和命题1,我们给出一个大度搜索优先算法,用来寻找具有较多叶子的生成树。记号N(X)表示集合X的邻点之集,并令N[X]=N(X)∪X。特别地,当X={u}时,直接写N(u)和N[u]。 大度优先搜索算法 (Largedegree-First Search Algorithm) 输入:具有顶点v1,v2,…,vn的无标度图G,且dG(vi) ≥dG(vi+1),i=1, 2,…,n-1,Δ(G)=dG(v1) >1。常数k满足δ(G) ③ 如果i ④ 采用BFS算法(Breadth-First Search Algorithm)。Hl是树或森林。令S←V(Hl);令R←N(X);对每一个顶点x∈S,有l(x)←0。 ⑤ 如果R=Ø和S=V(G),记找到的生成树为H,转到⑧。如果R≠Ø,转到⑥;如果R=Ø且S≠V(G), 转到⑦。 ⑥ 顶点v是R中第一个顶点,取w∈N(v)(R∪S),且w满足dG(w) ≥dG(x) (x∈N(v));把w放进R, 使其成为最后一个顶点;从R中取出v,然后把它放进S;令l(w)←l(v)+1;转到 ⑤。 ⑧ 输出生成树H。 定理3 大度优先算法输出H是生成树。 例3 应用大度优先算法的一个例子在图2和图3给出。在G1中,是选择常数k=11满足δ(G)<11<Δ(G),使得dG(v1)≥11,dG(v2)≥11,但对v∈V(G){v1,v2},有dG(v)<11。G1和G2是执行大度优先算法的前3步; 从G3到G8是执行大度优先算法的后5步。 图2 应用大度优先算法的一个例子Fig.2 An example of application of the large degree-first search algorithm 图3 G7 中的顶点u0⊆V(G)SFig.3 A vertex u0⊆V(G)S in G7 本文没有进行大度优先算法的复杂度确定,以及估计所找到的生成树叶子数目,这是今后要进行的研究。关于平衡集以及生成树,要进行的工作是:① 挖掘平衡集在无标度网络 (图) 中的深层次的功能。②在已知图有平衡集,快速找出所需要的生成树,如叶子最多或最少的生成树,最短直径的生成树等,探讨之间的联系性。③在一个无标度网络 (图) 中,平衡集中的点对无标度网络 (图) 的鲁棒性和脆弱性有什么影响?④寻找一个图的最小平衡集可以按照:(i) 先找出它的所有生成树,定义一个二维数组,用以保存所得生成树以及它的叶子集;(ii) 去掉原图中的叶子和割点,求出所剩余集合S的所有子集,定义一位数组,将所有子集保存;(iii) 用S的任意子集与 (i) 中的树集进行验证,得出最小平衡集。然而,这个算法是比较复杂的,但也是通用的算法。对于比较简单的连通图,可以根据这种思路编写通用的算法,需要做的是证明算法的正确性、可行性及其复杂性。 最后,提出下面的问题: 问题1 刻画具有最多叶子的生成树T1,T2,…,Tt的连通图G,使得 D(T1) 问题3 猜测“均匀”图没有真平衡集的网络,它的TM-平衡集也不存在。 [1] 刘大有, 李晶, 杨博. 信息传播网络学习方法[J]. 吉林大学学报:理学版, 2012, 50(4): 767-774. [2] 范淑艳, 韩卫占, 霍永华. MPLS网络的综合接纳控制算法[J]. 中山大学学报:自然科学版,2011, 50 (2): 54-57. [3] 刁玉平, 廖铭, 刁永平. 互联网架构关键资源可扩展研究[J]. 中山大学学报:自然科学版, 2011, 50 (6): 53-57. [4] 黄超, 王国利. 无线传感器网络协作无信标可靠路由协议[J]. 中山大学学报:自然科学版,2013, 52 (4): 39-44. [5] RADIA PERLMAN. Hierarchical networks and the subnetwork partition problem [J]. Computer Networks and ISDN Systems, 1985, 9: 297-303. [6] YAO B, ZHOU X Q, ZHANG J J, et al. Labellings and invariants of models from complex networks [C]// Proceeding of 2012 International Conference on Systems and Informatics, 2012:1616-1620. [7] YAO B, CHEN X E, ZHOU X Q, et al. Graphs related with scale-free networks [C]//Proceeding of The 2ndInternational Conference on Electronics, Communications and Control, 2012: 284-287. [8] YAO B, CHEN X E, YANG C, et al. Spanning trees and dominating sets in scale-free networks [C]// Proceeding of 2012 IET International Conference on Information Science and Control Engineering, 2012: 111-115. [9] YAO B, ZHANG Z F, WANG J F. Some results on spanning trees [J]. Acta Mathematicae Applicatae Sinica, English Series, 2010, 26(4):607-616. [10] FERNAU H, KNEIS J, KRATSCH D, et al. An exact algorithm for the maximum leaf spanning tree problem [J]. Theoretical Computer Science, 2011, 412 (45): 6290-6302. [11] GAREY M R, JOHNSON D S. Computers and intractability: a guide to the theory of NP-completeness [M]. New York : W H Freeman and Company, 1979. On Balanced Sets in Scale-free Networks (Graphs) LIUXia1,YAODongren2,YAOBing1,ZHANGWanjia1 (1.College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China; 2.College of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070,China) The scale-free nature of a scale-free network yields uneven distribution of connections (degrees) between its nodes. As the topological structures of scale-free networks are not exactly figured up to now, people can not observe clearly paths of information dissemination in scale-free networks. Based on the idea of using spanning trees in researching topological structures of scale-free networks, the universal structure of scale-free networks without relating time and sub-nodes are tried to find, and balanced sets that are extensively related with spanning trees in the networks are researched, and furthermore show an algorithm for finding spanning trees with more leaves. balanced set; connected graph; spanning tree; scale-free network 2014-02-08 国家自然科学基金资助项目 (61163054, 61163037, 61363060) 刘霞 (1990年生), 女;研究方向:组合优化和图论;通讯作者:姚兵;E-mail:yybb918@163.com 10.1347/j.cnki.acta.snus.2015.01.005 O A 0529-6579(2015)01-0019-05


1 结论及其证明
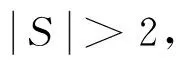




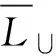


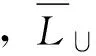
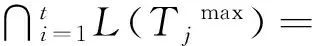
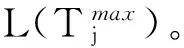

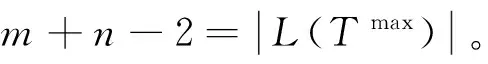




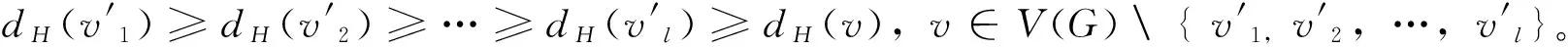

2 总结及今后的研究