Navier-Stokes方程在图像放大中的应用*

邹 杨，冯兆永，姚正安

(中山大学数学与计算科学学院，广东 广州 510275)



Navier-Stokes方程在图像放大中的应用*

邹 杨，冯兆永，姚正安

(中山大学数学与计算科学学院，广东 广州 510275)

利用基于流体动力学方程的模型进行图像放大处理。该模型有各向异性的扩散项和对流项，利用多种信息传播模式对未知信息进行填补。实验结果表明模型在图像放大处理的有效性。

图像放大；Navier-Stokes方程；各向异性扩散；块状效应

图像是获取信息的一条重要途径，对图像所包含信息进行分析和处理会依实际需求不同而不同。在某些情形下，需要修改图像分辨率并保证改变后的图像有较好的视觉效果，图像放缩技术此时起着重要作用。

图像放大是将低分辨率图像转化成高分辨率图像，图像缩小则是将高分辨率图像转化成低分辨率图像。在本质上两者并无差别，均是图像插值技术。图像插值的经典格式有多项式插值，三角多项式插值，样条插值等。此外，插值方法可以分为线性插值和非线性插值。线性插值有多项式插值里的最临近插值，双线性插值。线性插值的系数为常数，其不随节点的变化而变化，因此在图像放大后会出现边缘模糊和块状效应。非线性插值能克服线性插值的这些缺点，例如自适应插值[1]，边导数的插值方法等[2]。

偏微分方程根据扩散性质可以分为各向同性扩散和各向异性扩散。具体表现在扩散项系数为标量或者张量。当扩散项的系数为常数时，这为线性扩散，是各向同性扩散的简单情形[3]。而在图像处理中多认为线性扩散为各向同性扩散，其余情形为各向异性扩散。Morse等[4]利用水平集的平均曲率运动(MCM)进行图像放大，并取得较好效果。朱宁等[5]在2005年利用偏微分方程的热传导模型，提出基于一种新的热传导方程边值问题的图像放大模型，经此模型放大不会出现斑点，亮暗区域偏移的现象。2008年，邵文泽等[6]提出一种局部几何结构驱动的偏微分方程模型。2011年，祝轩等[7]提出曲率驱动与边缘停止相结合的非线性模型，该文将曲率作为一个控制传导率的因素。Kim等[8]提出一种基于偏微分方程的曲率插值算法，该方法能有效的减弱一般放大方法的边缘模糊和块状效应等不利影响。卫保国等[9]提出一种由方向扩散，冲击滤波和保真项构成的偏微分方程进行图像放大。姜东焕等[10]针对Chanbolle图像放大模型产生的块状效应，提出非局部的变分正则化图像放大模型。

You等[11]提出一个新的各向异性的四阶偏微分方程进去图像去噪，该模型能弥补二阶偏微分方程进行图像去噪产生的块状效应这一不足。宋锦萍等[12]利用该模型进行图像放大，实验表明模型在图像放大方面的有效性。Bertalmio等[13]给出Navier-Stokes方程模型进行图像修复。本文将利用该模型进行图像放大。

1 基于Navier-Stokes方程的图像放大

Bertalmio等[14]提出如下的一个三阶偏微分方程

ut=▽⊥u·▽L

其中L为微分算子，当L=Δu时，得到三阶非线性发展偏微分方程

ut=▽⊥u·▽(Δu)

(1)

该模型的传播原理是信息沿断裂水平线传播，在光学中则是沿等照度线方程传播，后者则是熟悉的一类传播模型的基础。

另一方面，在流体力学中所知，非线性运输或对流方程容易导致激波，为保证数值计算的稳定性，可以对方程做出一点改进。

在图像处理的偏微分方法中，有一大类的方程属于热传导方程及其改进的方程，其中有Perona-Malik类型的扩散方程。

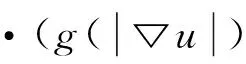
(2)

该方程将图像的滤波过程和图像边缘检测过程两者结合起来，而传统的图像处理中，两者是各自独立的过程。从扩散行为上分析，如果能选择好的函数g，该方程有可能实现图像平滑和边缘增强的作用。

从数值计算的角度看，P-M方程的右端项是黏性项，如果能在方程(1)加上该黏性项则能使得数值计算的稳定性得到一定的保证。

在分析二维不可压缩流体的涡方程后，发现上述两个方程能结合形成一个新的方程。首先，二维不可压缩流体的速度场v:Ω→R2是无散的，即

▽

其次，标量涡流w，即三维涡旋向量在某平面的投影，可以表示为

定义v⊥=(v2,-v1)为v的法向流，则

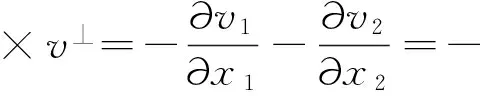
说明v⊥是无旋的，由Gauss-Green-Stokes定理，v⊥为某函数u的梯度流▽u=v⊥，u被称为流函数，由流函数可以得到涡旋标量的另一表示

w=▽·(v⊥)=▽·(▽u)=Δu

根据Navier-Stokes方程

vt+v·▽v=-▽p+μΔv

其中v是速度场，p是压强，μ是黏性系数。当μ=0时称为无黏流。

对上述方程两边同时用旋度算子作用，则得到涡流方程

wt+v·▽w=μΔw

(3)

方程(1)的右端正是涡流方程(3)左端第二项

v·▽w=▽⊥u·▽(Δu)

根据流函数的定义，黏性流方程(3)的稳定态满足下面的式子

▽⊥u·▽(Δu)≈0

上式说明流体是沿着Δu等照度线方向流动，这与图像信息沿等照度线方向传播到的原理是一致的。

将二维不可压缩流体力学中流函数和图像的灰度函数相对应，则得到图像修复模型，下表简要总结两者的关系。

表1 流体力学和图像处理物理量对应关系Table 1 Relation between fluid dynamics and image

如将方程(3)右端的黏性项用P-M黏性项替换，则得到

(4)

其中w=ΔI，v=▽⊥I，函数g是单调递减函数。

2 数值实验

本文将用如下方程进行图像放大

(5)

其中w0=ΔI0,v=▽⊥I,n是单位外法线向量，函数g是单调递减函数。方程(5)扩散稳定并更好地条件化了运输机制。

对方程(5)的数值计算，将采用隐式格式，关于时间用向前差分格式离散

▽wk+1)i,j=

(6)

上式中的黏性项用五点差分格式离散

(7)

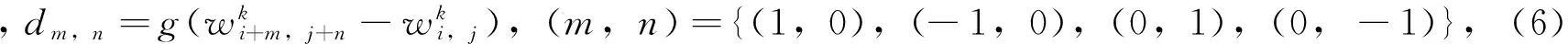
最后得到的差分方程(6)用交替方向迭代方法(ADI)求解。

关于Possion方程ΔIk+1=wk+1，采用五点中心差分格式离散，形成的线性代数方程组AIk+1=wk+1将用Jacobi迭代进行求解。与Possion方程不同，代数方程组中A是mn×mn的矩阵，Ik+1，wk+1是重新排列后的mn×1的向量。

计算流程如下：

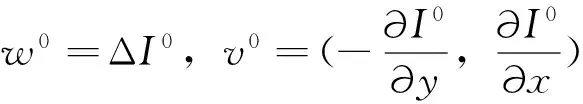
2)利用(6)得到wk；

3)求解Possion方程得到Ik；

4)由Ik计算vk；

其中k=1,2,…，满足一定条件迭代停止，得到的Ik是最终的结果。

下面用一些具体的数值实验结果展示模型在图像放大处理方面的有效性。

实验1 为观察模型在传播过程中的性质，用热方程(Laplace方程)放大4倍和本文模型放大4倍，见图1，从结果可以看出，热方程在放大的同时会产生比较明显的模糊和边缘不分段现象，这也是一些二阶模型的不足之处，本文模型能一定程度上改善这一不足。图中围巾有一定的纹理特征，两模型对纹理都没有体现出较好的处理结果。

图1 热方程和本文模型放大效果Fig.1 Zooming by different model

实验2 对Lena(128×128)的部分图像分别用文[14,16,17]和本文模型进行放大2倍处理，见图2，通过对结果比较的发现，文[14]的二阶模型在放大后在鼻梁、嘴唇、帽檐部分出现较为明显的块状效应，眼珠部分出现了一些灰度的偏移，在羽饰部分过渡的不够自然。本文和文[16,17]四阶模型能改善这些不足，但是都存在下巴处模糊的情况。

图2 Lena图放大2倍效果Fig.2 Lena image zooming by different model

实验3 对Jennifer(128×128)用文[14,16,17]和本文模型进行放大4倍处理，见图3。用文[14]模型处理后头发部分的灰度过度和信息的生成比其它模型要不自然，文[16]的四阶模型在头发和肩膀边缘部分有块状效应，这因为其在扩散方向的系数虽然不是常数，但是是一样的。本文的模型的黏性项也有同样问题，但是有运输项，能部分改善，但是同四阶模型相比，在放大更大倍数后，四阶模型的视觉效果会比较自然。

图3 Jennifer图放大4倍效果Fig.3 Jennifer image zooming by different model

为了比较各种模型的放大效果，把Camera,Pepper和Lena图像均为(256×256)缩小一半,然后用不同的模型进行放大两倍处理。将Lena缩至1/4，再放大4倍。缩小处理为下采样。在图像的客观评价体系中，峰值信噪比(PSNR)是一种比较接近人眼的视觉效果评价量。均方误差(RMSE)用来测量放大图像与标准图像的相近程度，给出模型的相关结果。

PSNR和RMSE的计算公式为

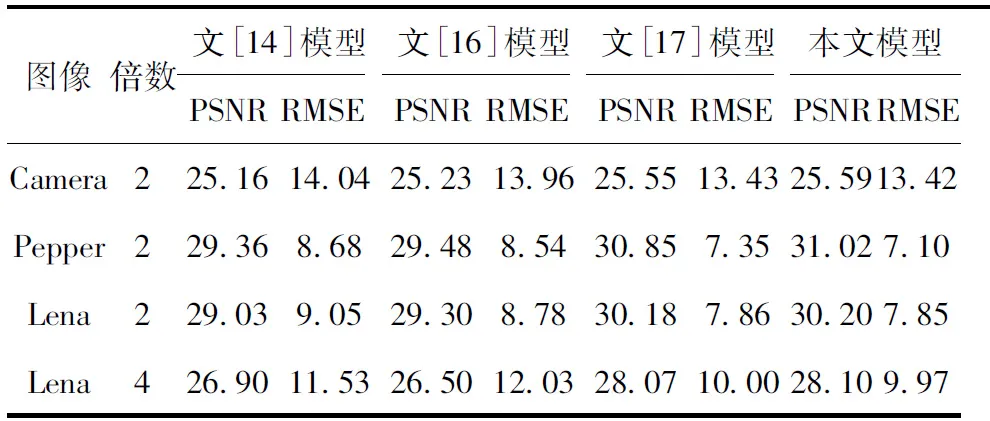
表2 不同模型放大处理的PSNR和RMSETable 2 PSNR and RMSE of different models

3 结 论

文中提到的模型有运输项和黏性项两种不同的信息传播方式，该模型是对图像的Laplace光滑度进行渐变，这与一类通过最小化Laplace光滑度的变分模型有一些类似，这类模型最终得到一类四阶方程，本文模型则是依照流体力学方程产生渐变。流体力学方程在演变一个很小的时间内，渐变具有一定的相似性，如油滴在水中扩散，在短时间内，油滴的形态有一定的相似性。通过这样的性质能在一定程度上保持Laplace光滑度形态，从而达到对未知信息的猜测。因流体力学方程的特点，模型在纹理方面效果不理想。实验结果说明模型在图像放大处理方面的有效性，对锯齿化效应和块状效应有一定的抑制作用。关于黏性项中扩散函数和黏性系数的作用还应通过进一步的实验分析清楚。现在有很多四阶方程模型的研究，能否把黏性项换成四阶黏性，以及同CCD模型的结合，能否与一些保持形态的变量相结合，找到更合理的数值计算方法将是随后的研究应注意的。

[1]GONGYG,WUXS.Anadaptiveimageinterpolationalgorithmbasedonedgeinformation[J].ComputerApplicationandSoftware, 2009, 26(4): 225-227.

[2]ZHOUDW,SHENXL.Edge-directedbicubiccolorimageinterpolation[J].ActaAutomaticaSincia, 2012, 38(4): 525-530.

[3] 王大凯，侯榆青，彭进业. 图像处理的偏微分方程方法 [M]. 北京：科学出版社, 2008.

[4]MORSEBS,SCHWARTZWALDD.Imagemagnificationusinglevel-setreconstruction[C]//ProceedingsofIEEEConferenceonComputerVisionandPatternRecognition,Kauai,Hawaii,USA:IEEEPress, 2001.

[5] 朱宁,吴静,王忠谦. 图像放大的偏微分方程方法[J]. 计算机辅助设计与图形学学报，2005,17(9): 1941-1945.

[6]SHAOWZ,WEIZH.Localgeometrydrivenimagemagnificationandsuper-resolution[J].JournalofImageandGraphics, 2008, 7(13): 1235-1243.

[7]ZHUX,LEIWJ,ZHANGSH,etal.Imagezoomingbycombinationofthecurvature-drivenandedge-stoppingnonlineardiffusion[J].ComputerScience, 2012, 3(38): 290-299.

[8]KIMH,CHAY,KIMS.Curvatureinterpolationmethodforimagezooming[J].IEEETransactionsonImageProcessing, 2011, 20(7):1895-1903.

[9]WEIBG,HUIWH.Imagemagnificationbyadaptivecouplingoforienteddiffusionandshockfilter[J].JournalofImageandGraphics, 2011,16(4): 533-537.

[10] JIANG D H, XU G B, DONGYE C L. Variational image zooming based on nonlocal total variation [J]. Journal of Computer Applications, 2012, 32(3): 725-728.

[11] YOU Y L, XU W Y, TANNENBAUM A, et al. Behavioral analysis of anisotropic diffusion in image processing [J]. IEEE Transactions on Image Processing, 1996, 5(11): 1539-1553.

[12] SONG J P, GAO R, ZHU F, et al. mage zooming algorithm based on partial differential equations technique [J]. Journal of image and Graphics, 2009, 1(14): 82-87.

[13] BERTALMIO M, BERTOZZI A L, SAPIRO G. Navier-Stokes, fluid dynamics and image and video inpainting [J]. IEEE Compute Vision and Pattern Recognition, 2001, 1: 355-362.

[14] BERTALMIO M, SAPIRO G, CASELLES V, et al. Image inpainting [C]∥Computer Graphics Proceedings, 2000.

[15] OSHER S, SETHIAN J. Fronts propagating with curvature dependent speed: algorithms based on Hamilton-Jacobi formulations [J]. Comp Phys, 1988, 79: 12-49.

[16] YOU Y L, KAVEH M. Fourth-order partial differential equation for noise removal [J]. IEEE Transactions on Image Processing, 2000, 9(10): 1723-1730.

[17] CARMONA R A, ZHONG S. Adaptive smoothing respecting feature directions [J]. IEEE Transactions on Image Processing, 1998, 7(3): 353-358.

Application of Navier-Stokes Equation in Image Zooming

ZOUYang,FENGZhaoyong,YAOZheng’an

(School of Mathematics and Computational Science, Sun Yat-sen University, Guangzhou 510275, China)

The model of image zooming based on fluid dynamics equation including convection term and diffusive term, have two ways of interpolation. The experimental results show the effective performance of the proposed model in image zooming.

image zooming; Navier-Stokes equation; anisotropic diffusion; blocky affect

2014-04-23

国家重点基础研究发展计划“973”基金资助项目(2011CB808002)；国家自然科学基金资助项目(10971234，11471339)

邹杨(1984年生)，男；研究方向：数字图像处理；通讯作者：冯兆永；E-mail:fzhaoy@mail.sysu.edu.cn

10.1347/j.cnki.acta.snus.2015.01.001

TN911.73

A

0529-6579(2015)01-0001-05