型号协作任务与资源的集成优化

□ 郝京辉 □ 龚杰峰 □ 于 洋 □ 孙进栋

北京航天动力研究所 北京 100076

航天液体火箭发动机的外包产品具有种类杂、数量多、批量不大等特点，产品研制过程的协作资源单位涉及航空、兵器、电子、科学院、研究所、高校、专业公司等多个领域，各单位的科研模式、科研资源和能力等各具特色。航天型号产品协作过程是协作任务单位根据具体的任务在市场中寻求分散的协作资源的市场活动，完全是一种市场化、开放性的经营行为，其过程本身是复杂多变的，需要从不同的角度去观察、分析，才能发现型号协作过程的规律与特征。

在产品协作过程中，协作资源的优化配置一直是人们关注的焦点，国内外学者针对这方面问题的研究也较多。如果研究的视野是产品协作的全部过程，实质上它们仅仅探索了过程中的一个方面，忽略了另外一个方面的问题，即协作任务优化问题。一些学者已经对任务的分解与重组展开研究,黎永前等［1］从供应链管理过程的角度描述产品协作任务，评价协作资源的能力，在此基础上对任务进行分解和优化。王伟等［2］按照产品结构树进行任务分解，用最小任务粒度集来划分协作任务，但对协作任务分解一类的问题，仅仅涉及任务的结构优化问题，而对任务参数的优化并没有展开讨论。沙磊等［3］从提高群体决策效率的角度出发，提出优化任务需求属性的方法，但是它仅仅能够确定任务需求属性的最佳变化趋势。另外一些学者研究了任务与资源的集成优化问题，程方启等［4］基于制造任务与资源之间的相互协调提出了协同制造链的概念，从制造任务属性参数角度出发，对协同制造链进行优化。周珂等［5］提出制造任务逐层分解与制造单元级资源配置协同优化的方法,建立了协同优化流程。

1 型号协作任务与资源的集成优化架构

在协作任务与资源优化的理论中，研究工作侧重于协作任务的结构和参数确定的情况，针对分散、动态的协作资源进行配置，即正向的优化过程。但是，在实际市场活动过程中，还存在着另外一个方向的优化——逆向优化过程，即协作任务的优化过程。正向优化与逆向优化过程所呈现出的结构是以型号协作过程的整体优化为目标，对协作资源与任务进行双向的优化过程。

型号协作任务单位可以根据市场上协作资源的特性、分布等情况，在与协作资源单位协商过程中逐步调整。优化任务结构和参数，完善任务的需求属性。在逆向优化过程中，最能够体现协作资源对任务属性要求的市场响应行为，是协作资源单位依据自身的综合能力所提出的完成任务指标参数，这些指标参数为市场处理任务参数优化提供了分析基础。协作任务结构的调整优化，对于逆向优化过程来说是一个重要的、阶段性的标志，因为当任务参数在现有任务结构框架下调整无效时，任务单位可以进行任务结构的重新构造。

型号协作任务优化与资源配置的解决过程并不是毫无消耗的过程，市场中的单位需要考量协作过程所耗费的时间、成本等。实际上协作资源配置与任务优化的联系是非常紧密的，在任务参数的逆向优化过程中，包含了非常多的协作资源配置信息，这些信息可以帮助市场中任务单位在进行任务优化活动的同时，开展协作资源的优选。因此，协作资源的配置必然是依托协作任务的优化过程而展开，并且与之相互协调地进行，具体的双向优化过程集成架构如图1所示。

2 集成优化的形式化描述

为了深入分析集成优化进程，将型号协作任务参数与资源的集成优化过程抽取出来，进行形式化的描述，为集成优化模型的构建奠定基础。

2.1 协作任务与资源优化活动

在型号协作过程中，协作优化活动是指正向优化与逆向优化过程中拥有明确目标的某一个进程，它服务于协作过程的整体过程优化。

据此，协作优化活动可以表述为一个四元组：

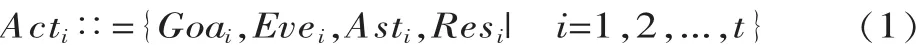
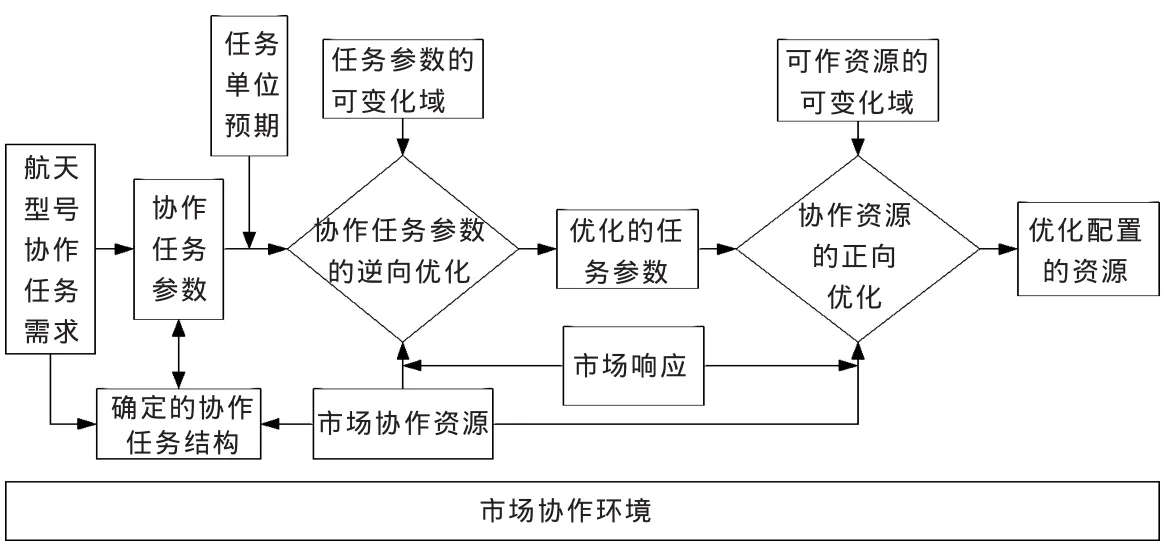
▲图1 双向优化过程的集成架构

式中：Acti为第i次进程中的协作过程活动；Goai为第i次进程中活动目标集合的表述；Evei为第i次进程中活动事件的集合；Asti为第i次进程中活动限定条件的集合；Resi为第i次进程中活动结果集合的描述。

2.2 协作资源空间

在型号协作过程中，协作资源空间是指协作市场中协作资源的结构、性能等特征，用一个二元组表示：

式中：MR_F为协作资源的结构，它描述型号协作资源的数量、分布、过程关系等特征；MR_P为型号协作资源的性能，它描述协作资源的功能、服务属性（加工成本、周期、质量等）等特征。

2.3 协作任务空间

在型号协作过程中，协作任务空间是指协作市场中协作任务的结构、参数，可以用一个二元组表示：

式中：MT_F为协作任务的结构，它描述协作任务的数量、过程关联等属性；MT_P为协作任务的参数，它体现了协作任务的市场表现形式。

在型号协作任务空间属性中，协作任务的关联属性特征是复杂的，它既包括了不同任务之间的关联、任务参数之间的关联，也包括了不同关联属性的关联关系，而且它们的属性可能表现出串行、并行或重叠等特征，更有可能是包含的关系。笔者重点分析型号协作任务的参数优化与资源配置的集成问题，所以完全可以假设协作任务已分解为可以独立操作的任务实体，在讨论任务参数优化问题时，可以忽略任务的联系属性约束。

2.4 协作任务参数的值域集合

在型号协作过程中，协作任务的每一个指标都有相应的参数值域，所有的参数值域构成了协作任务参数的值域集合，用RS表示，即：

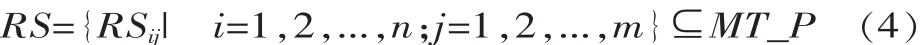
式中：RSij为第i个协作任务的第j个参数的值域。

2.5 协作任务预期参数

在型号协作过程中，任务单位经过市场调研，预期任务的完成参数称为协作任务预期参数，它可以表示为如下集合形式：

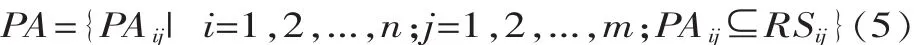
式中：PAij为第i个协作任务的第j个参数。

2.6 协作任务完成参数

在型号协作过程中，协作单位针对具体的任务，结合自身资源的属性特征，提出的任务完成参数称为协作任务完成参数，它可以表示为如下集合形式：

式中：PC（k）为第k个协作资源提出的协作任务完成参数集合；PC （k）ij为第k个协作资源提出的第i个协作任务的第j个完成参数。

2.7 协作任务参数的优化解集合

在型号协作过程中，结合协作任务完成参数与任务预期参数，优化任务参数的最优解集合称为协作任务参数优化解集合，它可以表示为：

式中：POij为第i个协作任务的第j个任务参数的优化解。

2.8 协作任务参数优化映射

在型号协作过程中，以协作任务完成参数与任务预期参数为基础，依据一定的约束条件，针对任务参数所进行的优化活动称为协作任务参数优化映射，它可以表示为：

MAP:（PC，PA）→PO|符合约束条件 （8）

2.9 协作资源配置解集合

在型号协作过程中，结合协作任务参数优化解与任务完成参数，进行资源配置所得到的最优解集合，称为协作资源配置解集合，它可以表示为：

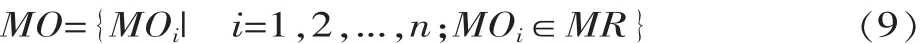
式中：MOi为某个进程中优选的第i个协作资源。

2.1 0 协作资源配置映射

在型号协作过程中，以协作任务参数优化解与任务完成参数为基础，针对协作资源所进行的配置活动，称为协作资源配置映射，它可以表示为：

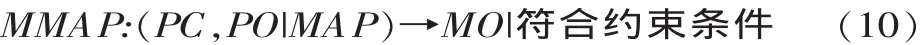
式中：MAP为协作任务参数优化的映射。

3 协作任务参数的逆向优化

3.1 协作任务参数优化数学模型

型号协作过程中针对协作任务参数的优化问题，可以借鉴数理统计中的数学期望与方差的概念。当协作单位提出参数PC时，针对第t个协作单位所提出的PC（t），可以考察任一任务参数 P 与 PC（t）的参数距离，它描述两个具有多维参数的指标的平均参数差距水平。进而，P与PC中每个PC（t）的平均参数差距的集成，可以理解为它衡量了PC相对于任一P的分布情况，即PC整体所表现出的稳定与波动、集中与离散的程度。显然该值越小，说明PC相对于P的分布越集中、越稳定，也就是说P所代表的任务参数越接近单位协作资源的实际能力供给情况，即说明P值越优秀。

3.1.1 任务参数距离

在型号任务协作过程中，对于任一任务参数P与第t个协作单位所提出的任务完成参数PC（t），如果将它们基于任务的序数展开为向量的形式，那么这两个向量之差的向量范数称为任务参数距离，记为Dt（P），即：

3.1.2 任务参数距离方差

在型号任务协作过程中，任一任务参数P与任务完成参数 PC 中每一个 PC（t）的 Dt（P）的总和，称为任务参数距离方差，记为D（P），即：

式中：ω=｛ωt=| t=1，2，...，q｝为协作单位的权重集合；ωt为第 t个协作单位的相对权重，ωt∈［0，1］。

可以看出协作任务参数距离方差D（P）是一种趋势距离。考虑到趋势距离D（P）越小，P越逼近PC，P值将越优秀，因此希望λi、ωt的取值趋势与此趋势相同，所以特此规定λi越小，意味第i个型号协作任务越重要；ωt越小，意味第t个协作单位越重要。

因为距离方差D（P）越小，P值越优秀，所以任务参数优化的目标函数是：

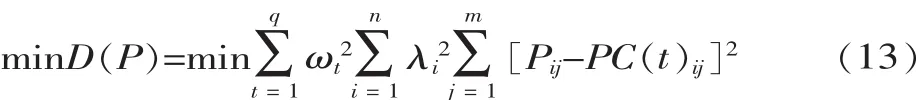
3.1.3 优化目标函数最优解存在定理

在型号协作过程中，对于任一协作任务完成参数集合 PC，即∀PC=｛PC（t）|t=1，2，...，q；PC（t）⊂RS｝，必然 存 在 一 个 P*=｛Pij*|i=1，2，...，n；j=1，2，...，m；Pij*∈RSij｝，使得 D（P*）达到协作任务参数优化目标函数的最小值 minD（P），即：minD（P）=D（P*），其中 P*∈PO。

证明省略。

3.2 优化模型的约束分析

对于任务参数优化目标函数的最优解P*，要求：

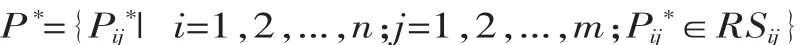
在型号任务协作过程中，任务预期参数PA与任务完成参数PC的距离方差称为任务参数标准距离方差，记为DS，即：

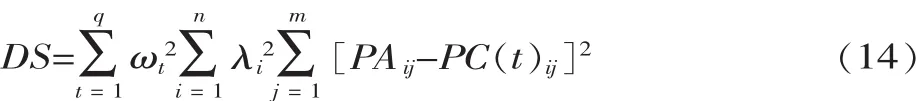
在优化目标函数的求解过程中，要求任务参数优化的结果 D（P*）＝minD（P）≤DS，这样的最优解才具有实际意义。

3.3 基于实数编码遗传算法的实现

协作任务参数属于结构型对象 （结构型对象是指集合、序列、矩阵、树、图、链和表等各种一维、二维、甚至多维结构形式的对象），它适合于用遗传算法来求解［6-7］。所以，笔者采用遗传算法对任务参数的优化模型进行求解。

（1）基于实数编码的策略。实数编码形式可以使编码和问题的解具有明显的对应关系，可理解性、可控制性非常好，所以采用基于实数编码的遗传算法来求解优化目标函数；

（2）种群多样性的策略。虽然在优化模型中种群中每个个体的参数都有相应取值空间的约束，但是为了保持种群的多样性，通过扩大初始种群的取值范围来达到此目的；

（3）保留优秀个体的策略。在满足种群多样性要求的前提下，为了提高求解的运算速度，按照一定的比例将当前种群中适应度最高的个体的结构完整地复制到下一代种群中；

（4）群体规模。假设群体规模为n，决策变量数为l，通常情况下有关系：1.5l≤n＜21/2；

（5）适应度函数。直接选择优化目标函数算式（13）作为适应度函数；

（6）选择算子。为了避免过早出现收敛现象和停滞现象，采用锦标赛的选择方法；

（7）交叉算子。对于实数编码遗传算法来说，常用的交叉算子有混合交叉算子、算术交叉算子、单峰正态分布交叉算子、边界交叉算子、基于方向的交叉算子等，笔者采用算术交叉算子；

（8）变异算子。对采用实数编码遗传算法来说，变异算子主要有：实数变异算子、非均匀变异算子、有向变异算子、高斯变异算子等，笔者采用高斯变异算子；

（9）遗传算子的参数设计。通常情况下，交叉概率Pc=0.20～0.80，变异概率 Pm=0.20～0.40；

（10）终止条件。采用最大进化代数T作为算法的终止条件。

4 集成优化的实现

在协作任务参数的逆向优化过程中，包含了非常多的资源配置信息，这些信息完全可以帮助任务单位在进行任务优化活动的同时，开展协作资源的优选，从而实现协作任务与资源的集成优化。

在型号任务协作过程中，当协作单位提出参数PC时，针对第t个协作单位所提出的PC（t），可以考察任一任务参数P与PC（t）的参数距离。以优化解P*为评判标准，计算PC（t）与P*的参数距离，将此距离作为单位优选协作资源的条件，参数距离越小，说明此协作资源具有符合协作任务要求的最佳条件。

引入算式（11）任务参数的距离 Dt（P），那么协作资源优化配置的目标函数为：

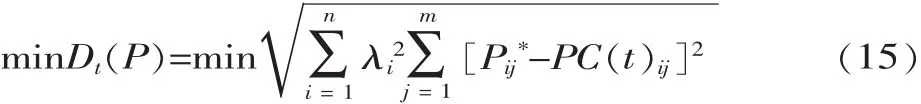
5 集成优化案例分析

5.1 协作任务参数的逆向优化

在某航天型号协作过程中，协作任务单位已经将该任务分解为4个可以独立进行运作的任务实体，它们分别是高压泵壳体、低压泵壳体、转动轴与轴密封组件，记为（TA1,TA2,TA3,TA4），其中每一项任务有3个参数：周期 Pe（单位：天）、费用 Ex（单位：万元）和质量Qu（单位：合格率%）。经过前期的调研，已经与6家有协作意愿的单位建立了联系，它们分别是MR1、MR2、MR3、MR4、MR5、MR6。

协作单位提供了它们对任务的完成指标参数，具体见表1。

表1 任务完成参数PC

协作任务单位提出了任务参数值域见表2，所提出的任务预期参数见表3。

表2 任务参数值域RS

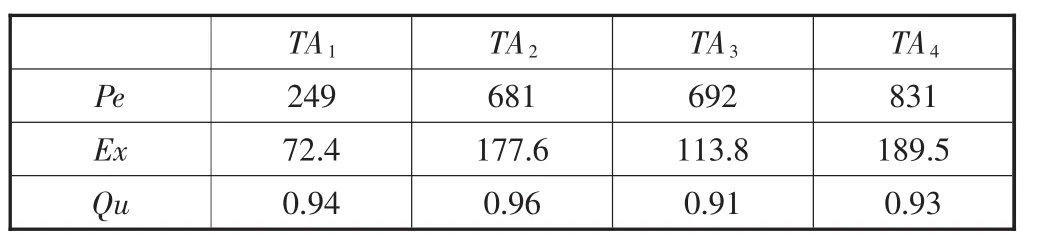
表3 任务预期参数PA

结合表3，由算式（14）可得：任务参数标准距离方差DS=5 869.13。

协作单位的权重ωi与任务的权重λi的取值见表4。

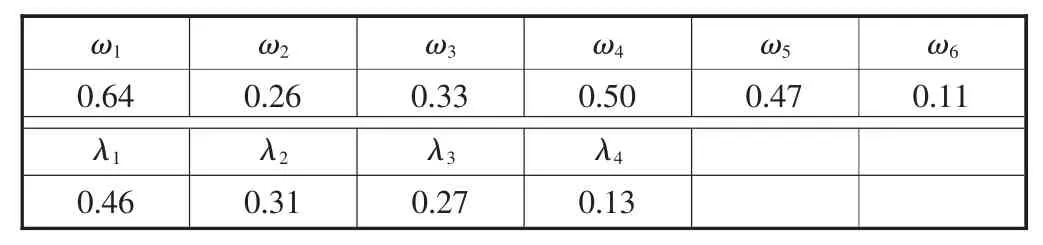
表4 权重参数

实数编码遗传算法的参数设计具体见表5，初始种群中每个个体的取值范围的设定见表6。

表5 实数编码遗传算法的参数

表6 初始种群的个体取值范围

采用基于实数编码的遗传算法在任务参数空间进行搜索，得到任务参数优化目标函数的最优值，即任务参数距离方差的最小值是：minD=4 321.985；得到优化目标函数的最优解，即最优个体（任务）为：

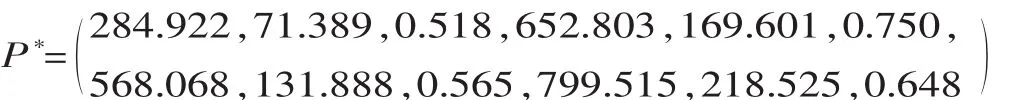
针对优化的结果，进行如下分析：

（1）参考表2可知，经过优化获得的最优个体Pij*∈RSij，说明得到的最优解 P*∈PO。

（2）比较优化结果minD=4 321.985与标准距离方差DS=5 869.13可知，minD＜DS，即任务参数优化的结果小于单位的预期值，说明任务参数的优化结果满足约束要求。

（3）如果从微观特征角度看，由最优个体P*可以获得优化后的协作任务性能参数，处理后见表7。

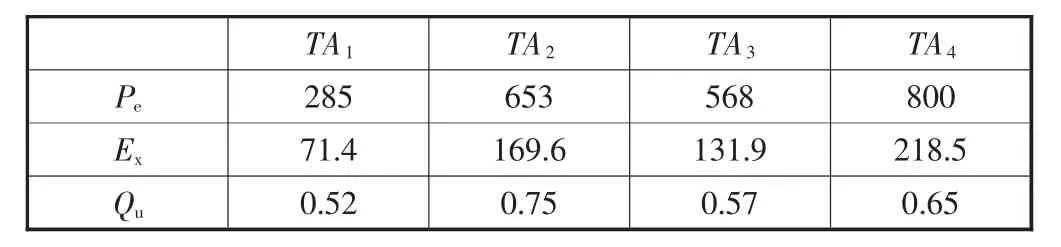
表7 优化的协作任务性能参数

比较表3与表7两组参数：协作任务预期性能参数PA与经过优化的最优协作任务性能参数P*，可以发现，优化得到的协作周期Pe普遍比单位预期的短，只有协作任务TA1的时间长，说明市场协作资源完成协作任务TA2、TA3与TA4的能力较强，而协作任务TA1比较难以完成。

优化得到的协作费用Ex比单位预期的有高有低，其中协作任务TA3与TA4的协作成本较高，说明完成协作任务TA3、TA4的时间虽然快，但是必须付出协作成本高的代价。协作任务TA2的成本较低，完成周期也较短，说明协作任务TA2比较容易实现。而协作任务TA1的完成成本相当，略有降低，但是它的完成时间却长，说明与上面得到的结论相同，协作任务TA1的完成技术难度较高。

优化得到的协作质量Qu比单位预期的普遍低，说明市场协作资源完成任务的质量普遍低于单位的预期。相对而言，协作任务TA2的完成质量最高，从而更加验证前面已经得到的结论，即协作任务TA2比较容易实现。而协作任务TA1的完成合格率最低，再次说明协作任务TA1比较难完成。

通过数据比较，可以对协作任务的市场响应特性进行归纳、总结，具体见表8。

表8 协作任务的市场响应特性

5.2 基于逆向优化的协作资源配置

型号协作任务单位在进行协作任务分析以及任务参数优化的活动过程中，可以同时开展协作资源的优化配置工作。

基于前面协作任务参数的过程及结果，引入已经得到的任务参数的优化解P*；同时，引入任务完成指标参数PC见表1，任务权重见表4。那么，根据式（15），可以得到每个协作资源的评判结果，具体见表9。

表9 任务确定环境下协作资源优化配置结果

从表9可以知道，第三家协作单位MR3的目标函数值最小，即在此进程中协作单位MR3应该是单位优先选择的对象。

6 结束语

航天型号任务协作过程存在双向优化结构，即协作任务优化与协作资源配置，该双向优化活动成为协作过程中的基本活动单元，描绘了航天型号研制过程的基本特征。型号协作过程是多属性的决策过程，是反复的、渐进的、螺旋式的演化过程，其中任务优化是协作的驱动力量，是协作组织组建过程的主要活动。通过协作任务参数距离与距离方差模型的提出，建立任务参数的逆向优化目标函数，该函数可以通过遗传算法进行求解。基于逆向优化过程，探讨资源配置活动的评判标准，建立相应的资源配置的正向优化数学模型，从而实现任务优化与资源配置的集成。

［1］ 黎永前，姜万生，朱名铨.供应链管理中产品任务分解优化策略［J］.机械科学与技术，2002，21（3）：479-481.

［2］ 王伟，易红，幸研，等.多环境下虚拟企业建立方法的研究与应用［J］.计算机集成制造系统，2005,11（3）：405-415.

［3］ 沙磊，徐晓飞，李全龙，等.基于遗传算法的动态联盟性能标准优化方法［J］.计算机集成制造系统，2002，8（6）：462-466.

［4］ 程方启，叶飞帆.基于制造任务参数距离模型的协同制造链优化构建［J］.中国机械工程，2011，22（2）：184-189.

［5］ 周珂，吕民，王刚，等.制造任务分解与制造单元级资源配置协同优化［J］.哈尔滨工业大学学报，2009，41（11）：47-52.

［6］ 玄光男，程润伟.遗传算法与工程优化［M］.北京：清华大学出版社，2004.

［7］ 周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999.