基于多故障模式及可靠缓存区的双设备模型系统性能分析

□ 张 孟 □ 范钦映 □ 梁春游 □ 周留洋

兰州理工大学 机电工程学院 兰州 730050

针对多故障模式下缓存区容量有限的双设备模型，提出了一种求解其生产能力的解析方法。多故障模式是指此双设备模型的上下游机器有多种故障方式，每一种故障方式都有相对应的MTTF（同一台设备，两次故障之间的平均工作时间）和MTTR（同一台设备从发生故障到正常工作的平均维修时间），用这两个参数来区分不同的故障方式。一台设备通常有多种故障方式，因为一台机器拥有许多零部件，每一个部件都有可能发生故障。以汽车自动组装线为例，每一个工作站都包含有：上料装置、夹紧装置、切削加工装置、进给装置等，这些装置的可靠性都是不同的，一旦发生故障，那么对应的维修时间、维修方式都是不同的。正是有了这样的情况，关于多故障模式下生产线的研究分析就具有实际意义。对于多故障模式下生产线的研究分析，单一故障模式的求解办法是综合多种故障方式对生产能力的影响，得到一个平均值，然后代入计算求解。但是，由于许多模型的MTTF和MTTR都是呈指数分布或是几何分布，单一故障模式的求解结果对生产能力给出一个近似的解析值，而不同故障方式对生产能力的不同影响却被忽略掉了。当缓存区容量很小时，生产能力的差别会很大，采用单一故障模型求解结果就不再可靠，换言之，单一故障模式的求解方法的适用性差。多故障双设备模型可以具体分析每一种故障方式对生产能力的影响。尽管分析双设备模型只是分析两台设备和一个缓存区组成的生产单元，但是，这种分析却是值得深究的。大型的生产线系统（Gershwin S B［1］；Dallery［2］；Tulliotolio，et al［3］） 是通过分解方法（Gershwin S B，et al［4］；Yeralan，et al［5］）或者综合方法（Dallery ，et al［6］；Gershwin S B［7］）来具体求解的，但是这两种方法都是以双设备模块为计算单元。更多方法参见文献［8～10］。针对多故障模式下缓存区容量有限的生产线，很多学者提出了自己的建模方法，参见文献［7，11～13］。 笔者受 Tulliotolio［14］所提模型的启发，对上下游均有两种故障方式的模型做出了具体的分析。仿真结果表明，本方法更准确可靠。

▲图1 双设备模型

1 模型描述

1.1 双设备模型

双设备模型由上游机器Mu、缓存区B、下游机器Md组成，如图1所示。每一个零件进入上游机器Mu，经过缓存区B和下游机器Md，最后离开此模型。上下游机器拥有相等的加工时间，传送时间忽略不计。缓存区容量有限，上游缓存区为空的机器所对应的状态记为饥饿，下游缓存区存满的机器所对应的状态记为阻塞，上游机器永不饥饿，下游机器永不阻塞，空闲状态的机器（处于饥饿或阻塞状态）不会发生故障。机器工作后，发生某种故障的概率是确定的，同一时间，一台机器只能发生一种故障状态。在一次工作循环中，一台机器在循环开始阶段故障，那么，此机器的维修率也是确定的。故障和维修均出现在循环开始，缓存区工件数目的变化发生在循环结束。工件不会被拒收或损坏，一台机器发生故障后，正在处理的工件自动返回上游缓存区，等待新一轮循环。

1.2 模型状态

假设此模型的状态为 （n，α1，α2），n 代表缓存区即时工件数目 （0≤n≤N），α1为上游机器的维修状态,α2为下游机器的维修状态。上游机器的正常工作状态为α1=1，否则 α1=μi（i=1，2，...，s），μi为机器的故障模式。同样的，下游机器的正常工作状态为α2=1，否则α2=μj，（j=1，2，...，t），μj为机器的故障模式。 机器处于状态（n，α1，α2）所对应的稳态概率记作 P（n，α1，α2），由于维修和故障在循环开始时发生，缓存区盈余水平的变化在循环结束时发生。缓存区的盈余水平为：

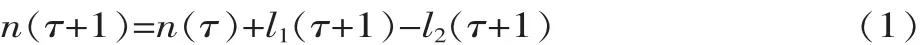
式中：τ为一次工作循环。

定义l1（τ+1）为上游机器在此工步结束时的加工件数；l2（τ+1）为下游机器在此工步结束时的加工件数。如果 α1（τ+1）=1，且 n（τ）＜N，则 l1（τ+1）=1，否则 l1（τ+1）=0；同样，如果 α2（τ+1）=1，且 n（τ）＞0，则 l1（τ+1）=1，否则 l1（τ+1）=0。

将正常工作的机器进入某一故障模式i的概率记为pui，那么，在一次工作循环中，机器经过维修可以正常工作的概率记为rui。同样， pdj、rdj分别代表下游机器的故障率和维修概率。上游机器所有故障模式的概率之和记为；下游机器所有故障模式的概率之和记为

1.3 生产能力的指标

衡量生产能力的指标是此双设备模型的生产率和缓存区的盈余水平，双设备模型的生产率记为E1、E2。E2指在某工作循环τ内下游机器Md正常工作的概率，E1指在某工作循环τ内上游机器Mu正常工作的概率，由于生产线具有连续性，所以上下游机器正常工作的概率是相等的，也即E1=E2。根据生产线产量的定义，E1=prob［（τ+1）=1，且 n（τ）＜N］；E2=prob［（τ+1）=1，且 n（τ）＞0］，进一步推导可得:

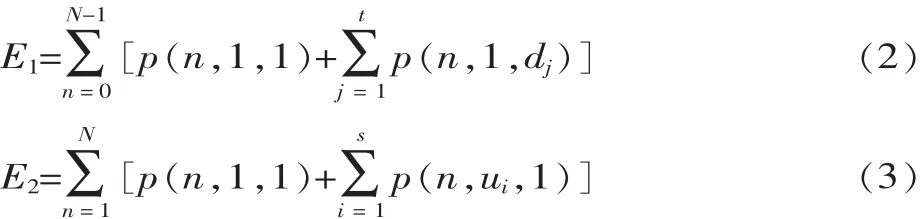
缓存区的盈余水平为：

故要衡量模型的生产能力，必须计算得到每一个状态的概率。

2 方程求解方法

此双设备模型共有 M=（s+1）（t+1）（N+1） 个状态，所以必须分析拥有M个状态的马尔可夫链。传统的思路是，求得M个关于这些状态概率的方程，建立方程组，求解这些未知数。但是，当N特别大的时候，这样的求解方法是行不通的。基于以上考虑，笔者提出了一种解析方法，本方法需要求解一个关于k的s+t次方程和一个s+t-1个方程的方程组。因此，本方法的数学计算量大大减少。本方法是对Gershwin,S.B.,1994［7］方法的一个扩展。核心思想是，首先对结果进行猜想，进而验证。验证过程为，将猜想的结果代入内部状态（2≤n≤N-2）方程，得到s+t组解。如果猜想是正确的，这些解的线性组合中肯定有一组会满足边界状态方程，那么这组线性组合就是要找的解。

2.1 内部状态变迁方程

分析此多故障双设备模型的马尔可夫链，可以得到以下状态方程：

受Tulliotolio［14］的启发，猜想内部状态的概率形式如下：

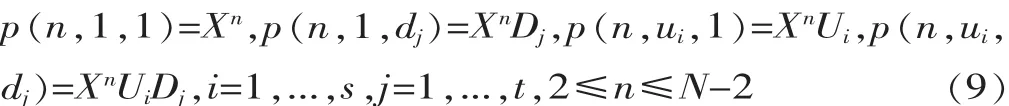
当 X、Ui、Dj一共有 1+s+t组，将式（9）代入式（5）～式（8），可以得到：

进一步简化后，假设：

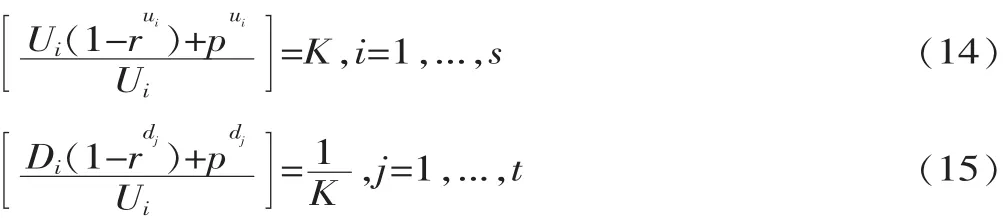
进一步整理，把 Ui、Dj代入式（11），可以得到：

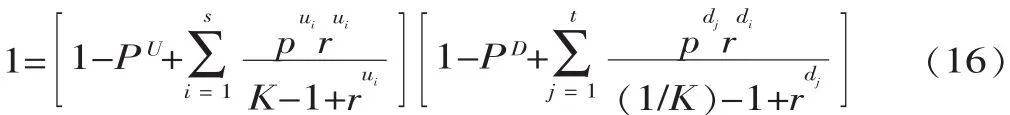
这是一个关于K的 （s+t）次方程。约定Km（m=1，...，s+t）为方程的第 m 个根,那么,Ui，m、Dj，m、Xm即为对应的解，整理可以得到：

假定所有的根Km都是实数,容易得到其中一个KR=1，代入式（17）有：

以上R组解满足内部方程，接下来寻找这些解来满足边界方程的线性组合。

2.2 边界状态

部分状态是暂时的，部分状态对应的稳态概率等于零，也就是说这些状态是暂时的，记为边界状态：

2.2.1 低边界状态变迁方程

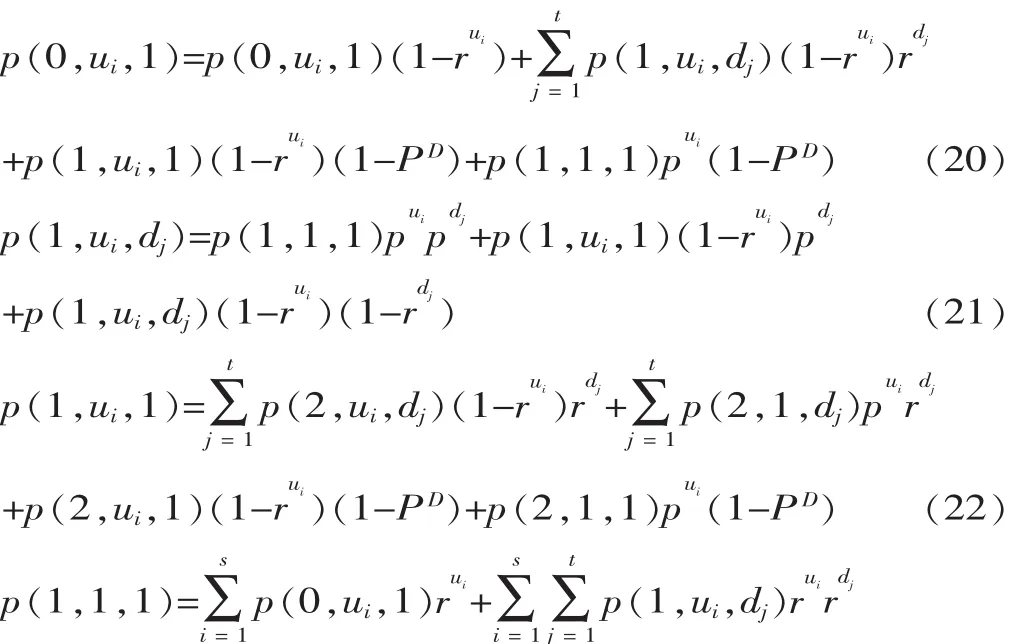
2.2.2 高边界状态变迁方程

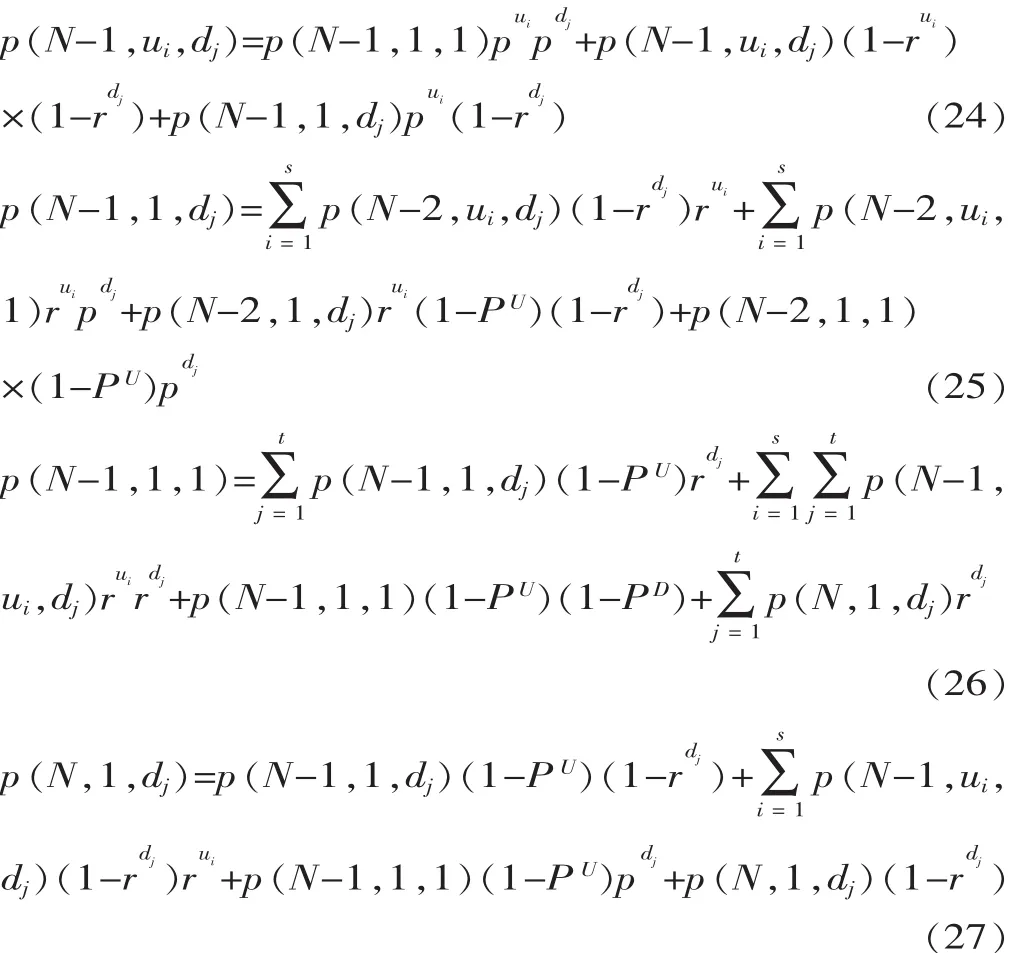
如果式（9）是合理的，那么一定能找到这些解满足边界方程的线性组合，猜想内部状态的概率符合以下形式：

式（22）、式（25）中：p（1，ui，1）、p（N-1，1，dj）只包含内部状态的概率，可以参照内部状态的概率公式计算，利用式（20）、式（21）、式（23）、式（24）、式（26）、式（27），可以把边界方程写成是关于常数C1,...Cm的函数：

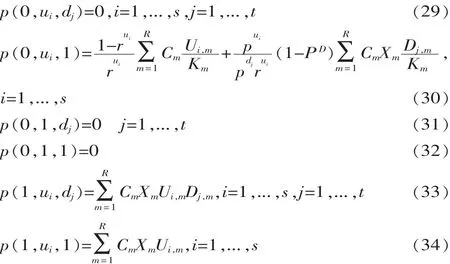
经过一系列处理，可以得到CR=0，将这些概率代入式（23）、式（26），可以得到：

所有的状态概率之和必须满足标准方程：

由式（45）～式（47）可以得到 1+s+t个方程组成的方程组，其中只有s+t+1个方程是与线性无关的。而未知数Cm（CR=0）也正好是1+s+t个，求解这个方程组，即可得到Cm。

3 求解方法

（1） 求解式（16），得到的所有根 Km（m=1，...，R）。

（2） 每个 Km可以产生一组 Xm、Ui,m、Dj,m， 通过式（17），求得 Xm、Ui，m、Dj、m。

（3） 求解由式（45）～式（47）组成的方程组，得到：Cm（m=1，...，R）。

（4） 通过式（28）～式（44），分别得到内部状态概率和边界状态概率。

（5） 通过式（2）～式（4），得到系统的性能评价指标E1、E2、n。

4 数据仿真

多故障模型方法针对性能指标的准确性，与Gershwin,S.B.［7］的单一故障模型分析作一对比。在基于单故障模型的分析方法中，每一台机器只有一种故障模式，而基于多故障模型的分析方法中，每一台机器有两种故障模式。

4.1 仿真参数

故障率和维修率之间的关系：

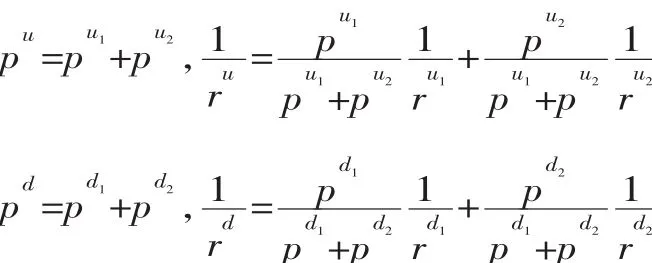
器故障率，ri代表机器维修率。

上下游机器的运行效率

可以得到上游机器的平均故障率、维修率和下游机器的平均故障率、维修率，也即单一故障模型的求解所需要的参数［7］。

4.2 仿真结果

图2中，虚线代表基于多故障双设备模型生产能力的解析结果，星型线代表基于单故障双设备模型生产能力的解析结果［7］。图2为平均产量与上游机器故障率ru1的关系图。图3为缓存区库存水平与上游机器故障率ru1的关系图。其中，rd1=0.09，rd2=0.09，pu1=pu2=0.005，eu=0.9，pd1=pd2=0.005，ed=0.9，N=10，ru=0.09，ru2随着ru1而变化，也即ru2可以用ru1和ru表示，这样，就可以得到系统性能随自变量ru1的变化关系。

▲图2 平均产量与上游机器故障率ru1的关系图

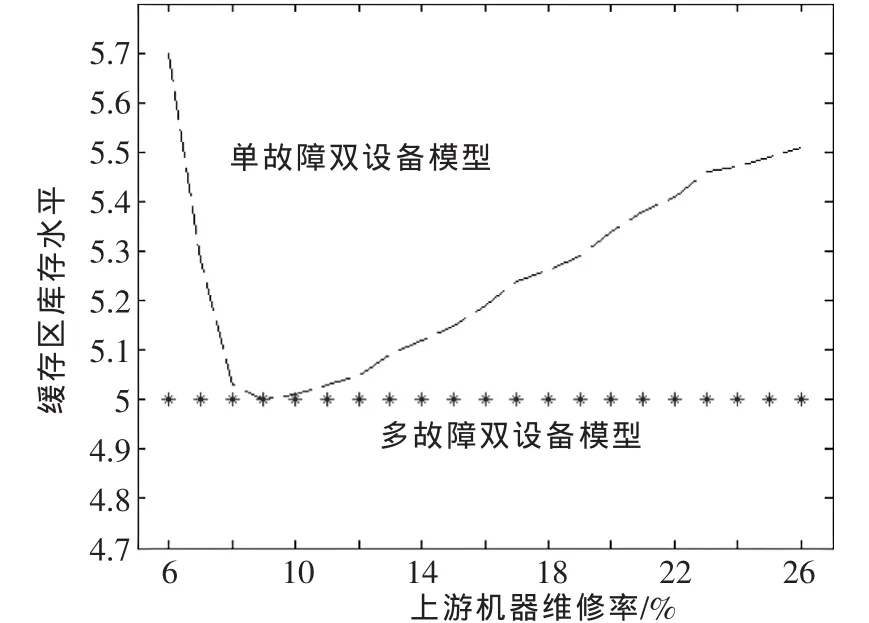
▲图3 缓存区库存水平与上游机器故障率ru1的关系图

通过仿真实验，可以看出，基于多故障双设备模型生产能力的解析方法得到的平均产量会随着上游机器维修率的变化而变化，当上游机器两种故障状态维修率相等时（ru1=ru2=0.09），系统的平均生产率达到最大，缓存区库存水平最小；当＜0.09时，平均产量随着ru1的增大而增大，缓存区库存水平随着ru1的增大而减小；当 ru1＞0.09时，平均产量随着ru1的增大而减小，缓存区库存水平随着ru1的增大而增大。而基于单故障双设备模型生产能力的解析方法得到的平均产量图和缓存区的库存水平不会随着上游机器维修率的变化而变化，只得到了近似解，这说明本解析方法更准确可靠。

5 结论

笔者以多故障双设备模型为主要研究对象，受Tulliotolio［14］所提模型的启发，结合对马尔可夫链和内部状态及边界状态的变迁关系的分析，提出了一种对多故障双设备模型生产能力的解析方法。对上下游均有两种故障方式的模型做出了具体的分析，并将本解析方法与基于单故障模式解析方法所得结果相比较，结果显示，在多故障模式下，本解析方法更准确可靠。

［1］ Gershwin S B.An Efficient Decomposition Method for the Approximate Evaluation of Tandem Queues with Finite Storage Space and Blocking ［J］.Operations Research,1987,35（2）：291-305.

［2］ Y Dallery,R David,Xiao Lan Xie.An Efficient Algorithm for Analysis of Transfer Lines with Unreliable Machines Finite Buffers ［J］.IIE Transactions,1988,20（3）：280-283.

［3］ Tullio Tolio,Matta A ，Jovane F.A Method for Performance Evaluation of Automated Flow Lines ［J］.Consumer Intelligence Research Partners Annals-Manufacturing Technology,1988,47（1）：373-376.

［4］ Gershwin S B， Schick I C.Modeling and Analysis of Three-Stage Transfer Lines with Unreliable Machines and Finite Buffers ［J］.Operations Research,1983,31 （2）：354-377.

［5］ S Yerelan,B Tan.A Station Model for Continuous Materials Flow Production Systems ［J］.InternationalJournalof Production Research,1997,35（9）：2525-2541.

［6］ Dallery Y,Gershwin S B.Manufacturing Flow Line Systems:a Review of Models and Analytical Results ［J］.Queueing Systems,1992,12（1-2）：3-94.

［7］ Gershwin S B.Manufacturing Systems Engineering ［M］.Upper Saddle River,Prentice Hall,1994.

［8］ Kim J,Gershwin S B.Integrated Quality and Quantity Modeling of a Production Line［J］.Operations Research Spectrum,2005,27（2）：287-314.

［9］ Poffe Andrea,Gershwin S B.Integrating Quality and Quantity Modelling in a Production Line ［R］.MIA Operations Research Center,2005.

［10］ Soares A D S,Latouche G.Matrix-analytic Methods for Fluidqueues with Finite Buffers ［J］.Performance Evaluation,2006,63（4-5）：295-314.

［11］ Ignall E,Sehick A.The Output of A Two-Stage System with Unreliable Machinesand Limited Storage ［J］.American Institute of Industrial Engineers Transactions，1977,9 （2）:183-188.

［12］ Shantikumar J，Tien C.An Algorithmic Solution to Two-Stage TransferLines with Possible Scrapping ofUnits ［J］.Management Science,1983,29（9）：1069-1086.

［13］ Jafari M A，Shanthikumar J G.Exact and Approximate Solutions to Two-Stage Transfer Lines with General Uptime and Downtime Distributions ［J］.IIE Transactions,1987,19（4）：412-419.

［14］ Tullio Tolio,Matta A，Gershwin S B.Analysis of Twomachine Lines with Multiple Failure Modes ［J］.IIE Transactions，2002,34（1）:51-62.