小型双足机器人步态规划研究

□ 杨 萍 □ 樊 迪

兰州理工大学 机电工程学院 兰州 730050

21世纪以来，国内外对机器人技术的发展越来越重视，机器人技术被认为是对未来新兴产业发展具有重要意义的高端技术之一［1］。双足机器人是机器人领域最活跃的研究热点之一，因其外形和功能形似人类，适合在人类生活和工作的环境中与人类协同工作［2，3］，还可以代替人类在危险环境中作业，拓宽人类的活动空间［4］，有高度的适应性与灵活性。实现稳定步行是双足机器人研究的首要任务［5］，合理的步态规划是机器人稳定步行的基础。因此，步态规划是双足机器人研究的关键技术之一，对其研究具有重要的理论意义和应用价值。笔者建立双足机器人的运动学模型，根据步行要求，采用三次样条插值方法规划出双足机器人各关节在整个步行周期内的平滑运动轨迹。

1 双足机器人运动学建模

建立双足机器人运动学模型是步态规划、稳定性分析的基础。笔者研究的对象是SHR-8S小型双足机器人，该机器人共有17个自由度，全部为转动关节，每条腿有5个自由度。其中，髋关节有2个自由度，1个负责前向运动，用于移动两腿实现迈步，使上半身前倾或后仰，1个负责侧向运动，使上半身侧倾；膝关节有1个自由度，负责前向运动，用于完成小腿的屈、伸动作；踝关节有2个自由度，1个负责前向运动，1个负责侧向运动，用于与髋关节配合并调整脚掌与地面的接触状态，完成步行过程。用Denavit-Hartenberg运动学表示法［6］建立机器人下肢坐标系，如图1所示，关节i的轴线与Zi+1轴重合，Xi+1轴与从Zi+1轴指向Zi+2轴的公共法线重合，Yi+1轴按照右手法则确定，坐标原点取Xi+1和Zi+1的交点。将机器人步行的起点位置设为世界坐标系［7］的原点，规定：X轴为机器人前向运动的方向，Z轴垂直向上，Y轴根据右手法则得到。为方便计算，将踝关节的两个坐标系、髋关节的两个坐标系分别建立在同一点；在左右脚分别以踝关节中心在地面的投影为坐标系原点固连一个参考坐标系；将两髋关节中心设为辅助坐标系的原点，运用辅助坐标系可以获得下肢各关节与躯干位置的联系，并且可以把上肢与下肢联系起来。

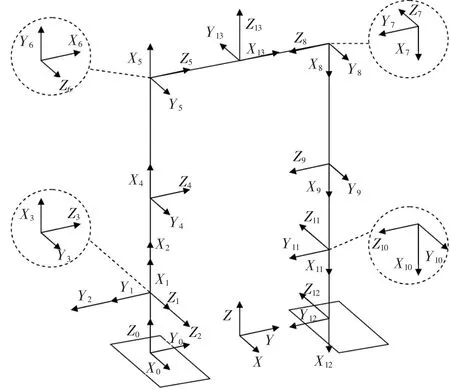
▲图1 机器人下肢坐标系图

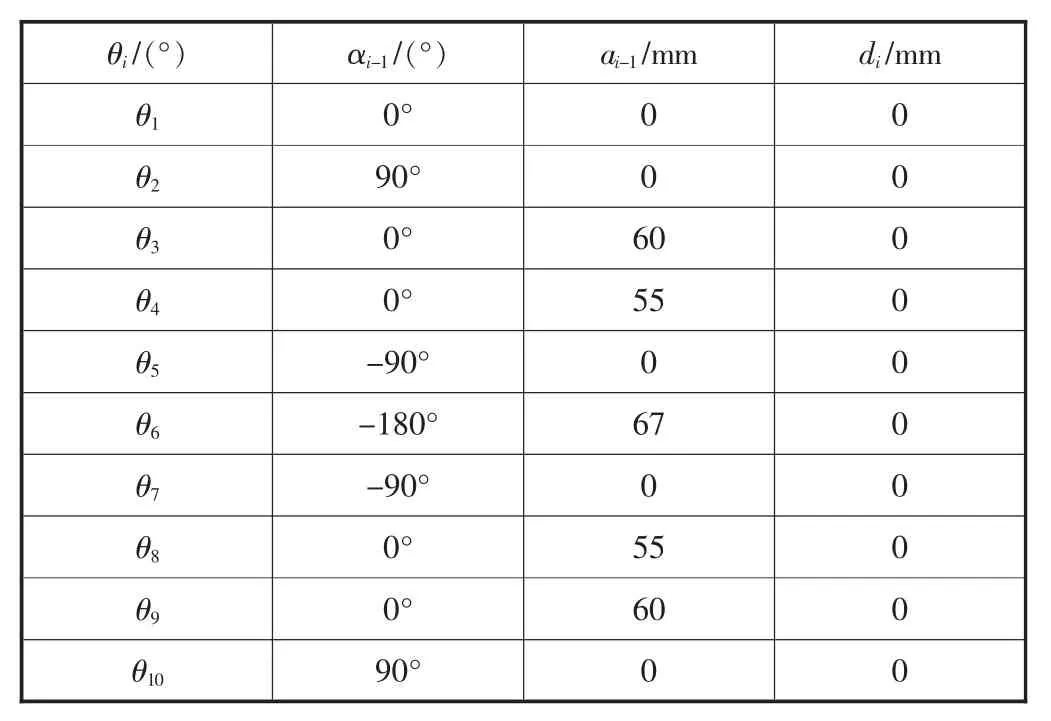
表1 D-H参数表

确定各连杆的关节变量和D-H参数，由于所有关节均为转动关节，所以关节角θi为关节变量，其它3个连杆参数即连杆扭角αi-1、连杆长度ai-1、连杆偏距di为固定值，双足机器人下肢的D-H参数见表1。

双足机器人正运动学是基于齐次变换矩阵的方法，根据机器人各关节的位置，求解摆动脚相对于参考坐标系的位姿。根据齐次变换理论，坐标系｛i｝与它相邻的坐标系｛i-1｝之间的连杆变换矩阵［8］为：

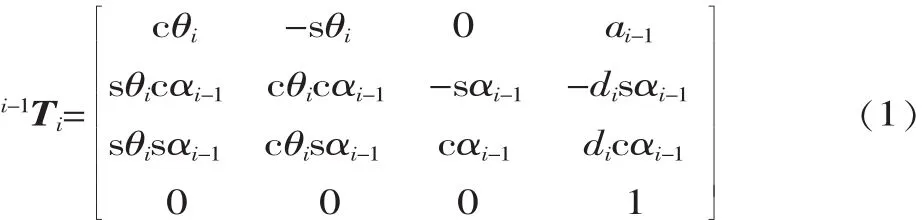
式中：s表示sin，c表示cos。将机器人下肢的D-H参数（表1）代入式（1），即可得到相应的齐次变换矩阵：

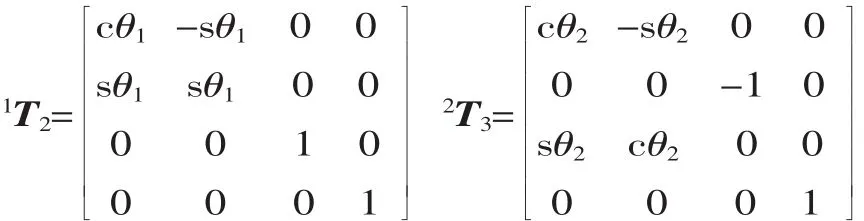
右脚踝关节中心的坐标系1到右脚踝关节中心在地面的投影点处的坐标系0之间的齐次变换矩阵为：

髋关节中心的坐标系13到右髋关节中心的坐标系6之间的齐次变换矩阵为：

综上所述，躯干任意时刻相对于右脚参考坐标系的位姿为：0T13=0T11T22T33T44T55T66T13；左脚相对右脚参考坐标系的位姿为：0T12=0T11T22T33T44T55T66T77T88T99T1010T1111T12。双足机器人逆运动学是给定摆动脚相对于基坐标系的位姿，求解各关节对应的运动角度。

2 三次样条插值函数

早期工程师制图时，将富有弹性的细长条（样条）在样点上固定，其它地方让它自由弯曲，然后沿样条边缘画出的曲线称为样条曲线。样条插值是一种常用的得到平滑曲线的插值方法，三次样条插值（Cubic Spline Interpolation）是其中应用较为广泛的一种。

设机器人某一关节在初始时刻ts的运动角度为θs，设计该关节在tf时刻的运动角度为θf。用待定系数法列出如下三次多项式方程：

对式（5）求一阶导数，得出如下方程：

将初始和末端时刻的运动角度 θ （ts）=θs、θ （tf）=θf代入式（5），将初始和末端时刻的关节运动速度 θ˙（ts）=βs，θ˙（tf）=βf， 代入式（6），得到：

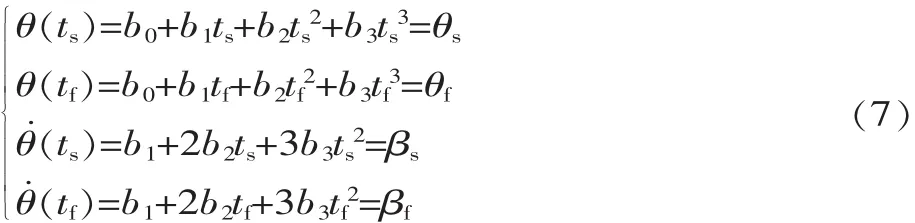
联立求解式（7）方程组，可解出式中 b0、b1、b2、b34个系数的值，只要将三次多项式的自变量即时间值代入式中，就可求得对应时刻的关节运动角度。

3 双足机器人关节轨迹规划

双足机器人一个完整的步行过程可分为3个阶段，分别是：起步阶段、周期步行阶段和止步阶段。本文重点研究双足机器人的周期步行阶段，步行过程如图2所示。图中右腿为支撑腿，用虚线表示；左腿为摆动腿，用实线表示。一个步行周期包含双腿支撑周期和单腿支撑周期，图2中A→B、C→D阶段为双腿支撑周期，指的是从摆动腿脚跟接触地面到支撑腿脚尖离开地面的时间段，在此期间，双足机器人完成重心的转移，双腿支撑周期一般占整个步行周期的20%左右［9］；图2中B→C→D阶段为单腿支撑周期，指的是摆动腿的脚离开地面到再次着地的时间段。

SHR-8S双足机器人的前向步行过程为：双腿支撑→右腿支撑→左腿摆动→双腿支撑→左腿支撑→...只要将图2中A→E阶段的步态确定，则左腿为支撑腿，右腿为摆动腿的步态可由A→E阶段的步态延时一个步行周期即可得到，双足机器人的步态完全确定。

笔者在前向平面内分别对摆动腿的脚掌、踝关节、髋关节的运动轨迹进行规划，并根据几何关系算出膝关节的运动轨迹，其它关节的运动角度可通过求解逆运动学方程得到。

▲图2 双足机器人周期步行阶段步行过程图

3.1 脚掌倾角规划

在图2所示的周期步行阶段，设步行周期为Tc，其中双腿支撑周期为Td，单腿支撑周期为Ts，第k步的时间为从kTc到（k+1）Tc，k为正整数，脚掌与地面倾角的变化如图3所示。在脚底始终平行于地面的情况下，脚底突然与地面接触时冲击力过大，非常容易导致步行失败，所以设摆动脚脚掌离地时与地面的夹角为qb，摆动脚脚掌着地时与地面的夹角为qf。

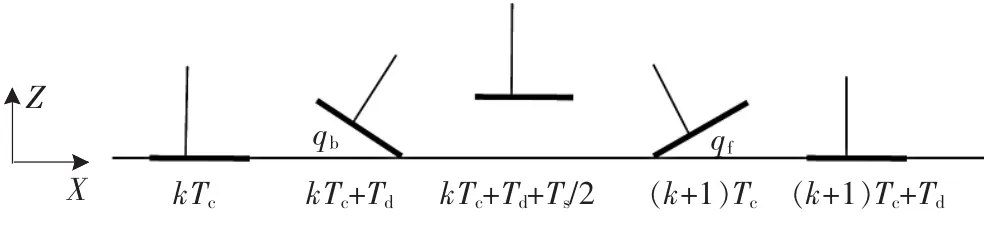
▲图3 脚掌与地面倾角变化图

前向平面上脚掌倾角的约束条件为：

选取脚掌与地面的倾角q（t）为三次样条插值函数，选取第一类边界条件，即：

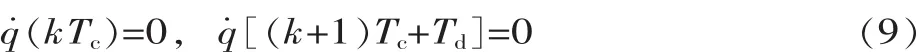
即认为在kTc和（k+1）Tc+Td时刻，脚掌的速度为零。利用三次样条插值函数规划出的脚掌倾角角度如图4所示。

▲图4 脚掌倾角角度图

3.2 踝关节规划

设摆动脚踝关节在kTc+Td+Ts/2时刻达到最高点，位置坐标为（Lm，Hm）。 设 Ds为步长，Lh为踝关节到脚底的距离，Lf为踝关节在脚底的投影点到脚尖的距离，Lb为踝关节在脚底的投影点到脚跟的距离。前向方向上踝关节的约束条件为：

选取第一类边界条件，即：

利用三次样条插值函数规划出的踝关节在X、Z方向的运动轨迹如图5所示。

▲图5 踝关节运动轨迹图

3.3 髋关节规划

髋关节的轨迹规划在整个步态规划中有关键的作用，影响整个机器人步行过程的稳定性。设髋关节在双腿支撑期的中间时刻达到最低点Hmin，在单腿支撑期的中间时刻达到最高点Hmax。则Z方向上髋关节的约束条件为：

设摆动脚离地时支撑脚踝关节到髋关节在X方向上的距离为xf，摆动脚着地时支撑脚踝关节到髋关节在X方向上的距离为xb。则X方向上髋关节的约束条件为：

髋关节应满足以下边界条件：

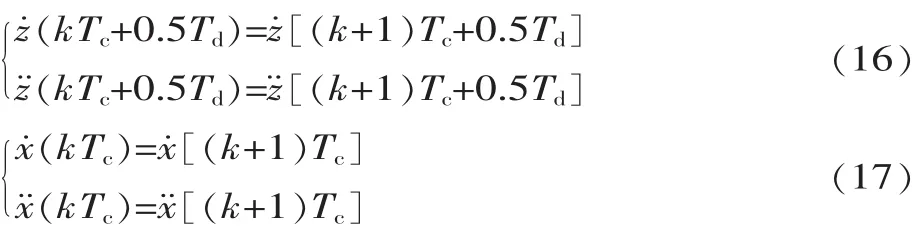
利用三次样条插值函数，根据式（14）、（15）的约束条件和式（16）、（17）的边界条件，对Z方向上的髋关节轨迹进行规划。

3.4 膝关节规划

已知踝关节、髋关节的运动轨迹，可以由几何关系推导出膝关节的运动轨迹。如图6 所 示 ，Ph、Pk、Pa分 别 表 示 髋 关节、膝关节和踝关节，膝关节的坐标为Xk、Zk，髋关节的坐标为Xh、Zh， 大腿L1= PhPk， 小腿L2=PkPa。

求得膝关节的坐标为：

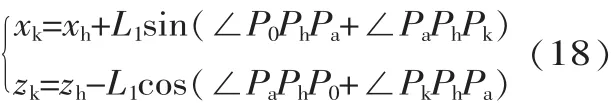
4 结束语

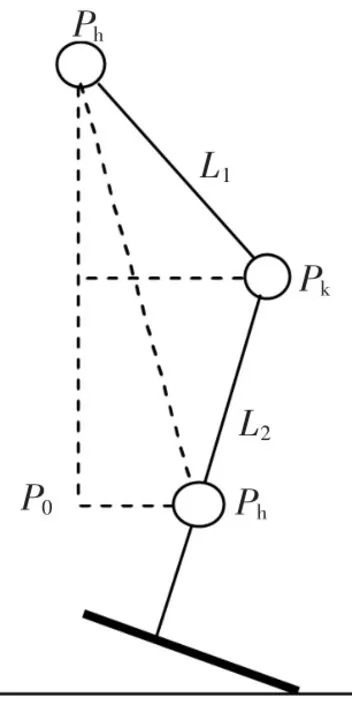
▲图6 腿部各关节几何关系图

本文采用Denavit-Hartenberg运动学表示法建立了SHR-8S小型双足机器人下肢的运动学模型，简要介绍了三次样条插值函数，在前向平面内利用三次样条插值函数分别对摆动腿脚掌、踝关节和髋关节进行轨迹规划，并由几何关系推导出了膝关节的坐标。Matlab的仿真结果表明，利用三次样条插值方法规划的步态，能保证规划轨迹的平滑，是合理可行的。

［1］ 徐扬生.智能机器人引领高新技术发展 ［N］.科学时报，2010-08-12.

［2］ Hirai K，Hirose M，Haikawa Y，et al.The Development of Honda Humanoid Robot ［C］.Proceedings of the IEEE InternationalConference on Robotics and Automation，Leuven，Belgium，1998.

［3］ Hirai K.Current and Future Perspective of Honda Humanoid Robot ［C］.Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems， Grenoble，France，1997.

［4］ 陈恳，付成龙.仿人机器人理论与技术［M］.北京:清华大学出版社，2010.

［5］ 刘志远.双足机器人动态行走研究［D］.哈尔滨:哈尔滨工业大学，1991.

［6］ John J Craig.Introducion to Robotics:Mechanics and Control， Third Edition［M］.Beijing:China Machine Press， 2006.

［7］ 梶田秀司，管贻生，译.仿人机器人［M］.北京:清华大学出版社，2007.

［8］ 蔡自兴.机器人学（第二版）［M］.北京:清华大学出版社，2009.

［9］ Huang Q， Kajita S.A High Stability Smooth Walking Pattern for a Biped Robot ［C］.Proceedings of the IEEE InternationalConference on Roboticsand Automation，Detroit，1999.

［10］吴泽琦.仿人足球机器人步态规划研究［D］.杭州：浙江工业大学，2013.