滚珠丝杠传动特性与刚度特性研究

□ 王 琦 □ 赵 飞 □ 张 驰 □ 谢质彬

1.中国科学院 宁波材料技术与工程研究所 浙江宁波 315201

2.宁波大学 机械工程与力学学院 浙江宁波 315211

滚珠丝杠是实现直线和旋转运动相互转换的重要部件，一般由丝杠、螺母、滚珠、回珠器等构成，其传动具有平稳、效率高、精度高、负载能力强、寿命长等特点，因此在机床直线进给系统中广泛应用。然而，随着数控机床向高精度、高速度方向的发展，使丝杠-滚珠-螺母在运动传递过程中的动力学和运动学状态参数变得复杂，影响到滚珠丝杠运动平稳性［1］。Chin Chung Wei等［2］，对滚珠丝杠传动过程中各部件间的相对速度、摩擦力、效率、滑动速度等进行了分析，指出了滚珠丝杠的接触角、变形等在外力影响时的变化规律。Yang T C等［3］利用第二类拉格朗日方程，建立滚珠丝杠传动系统动力学模型，对丝杠螺母的接触刚度等进行了研究。笔者通过对滚珠丝杠的传动特性和刚度特性的研究，重点分析了影响传动精度的因素，滚珠与螺母和丝杠接触点速度偏差对运动平稳性的影响，以及螺旋升角、接触角、负载变化等参数与接触变形的关系。

1 滚珠丝杠传动特性

1.1 滚珠丝杠传动精度影响因素

在丝杠旋转使滚珠推动螺母运动的过程中，滚珠产生绕丝杠的公转和自身在滚道中的自旋运动。在丝杠-滚珠-螺母的运动传递过程中，丝杠、滚珠、螺母间将产生接触弹性变形。将丝杠、螺母、滚珠作为刚体，对其空间运动过程进行建模，如图1所示，建立相对运动坐标系，并对其空间运动进行描述。在此，建立3个空间坐标系。

第一坐标系X′（x′，y′，z′）的 Z′轴与滚珠丝杠的轴线重合，坐标原点设在轴线与滚珠丝杠某一横截面的交点处，X′Y′平面与该横截面重合，用于描述各零部件的相对空间位置。第二坐标系X（x，y，z）用于描述滚珠丝杠绕轴线的旋转运动，第一、二坐标系间相差角度Ω。按照刚体运动学，由第二坐标系X到第一坐标系X′的变换为：

▲图1 滚珠丝杠零部件相对位置坐标系

式中：cΩ=cosΩ，sΩ=sinΩ，以下各处均采用相同标记。

假设滚道内其中一个滚珠沿滚道在X坐标系下旋转了θ角，根据式（1）可知，滚珠球心与X坐标系原点构成的矢量坐标在绝对坐标系X′下的坐标为：

式中：tanα=L/（2πrm），rm为滚珠丝杠的公称半径； L 为滚珠丝杠导程；α为滚道的螺旋升角。

定义 Frenet坐标系 Y（t，n，b），如图 1 所示，T 轴沿滚道的切向，NB平面位于滚道的截面，N轴指向球心方向坐标系X与坐标系Y间的欧拉角为［π/2，α，θ］。因此，坐标系X与坐标系Y间的坐标变换关系为：

由于滚道的限制，滚珠只能沿滚道在Y坐标系的T方向运动，受驱动力与负载的作用，滚珠、螺母和丝杠均会产生接触变形，滚珠与丝杠和螺母的接触形式如图2所示。假设变形仅会改变丝杠的相对转动角度和螺母在绝对坐标系下Ptz=0的位置，而不会改变滚珠球心在Y坐标系中的位置。考虑滚珠的接触变形δj（j=A，B），丝杠与滚珠接触点在Frenet坐标系下的坐标为:

▲图2 滚珠与丝杠和螺母的接触形式

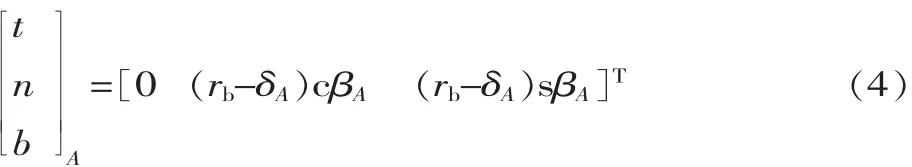
同样，螺母与滚珠接触点在Frenet坐标系下的坐标为:

式中：βi（i=A，B）为接触矢量与坐标轴N间构成的接触角；rb为滚珠半径。

对式（4）、式（5）进行坐标变换，可知接触点 A、B在绝对坐标系X′下的坐标分别为:

由式（6）、式（7）可知，螺母和丝杠间的相对位置将因接触变形而发生变化，因此在运动传递过程中，动态传动精度将受负载波动及驱动力变化的影响，而静态定位精度及重复定位精度不会受到影响。在动态传动过程中，滚珠丝杠的传动精度将受接触变形、接触角、螺旋升角、滚珠半径、丝杠半径、导程等参数的影响。

1.2 传动过程速度分析

在滚珠丝杠运动转换过程中，由于驱动力波动，制造误差等因素会造成滚珠受力幅值的变化，从而导致工作台速度的波动。同时，在运动转换过程中，滚珠不仅有绕丝杠的旋转运动，还有自身绕球心的旋转运动。设其自旋运动的角速度为 ω=［ωtωnωb］T， 其中 ωi（i=t，n，b）为滚珠绕 Y 坐标系的 T、N、B 各轴旋转的角速度。

在X′坐标系下，滚珠（上）与丝杠接触点Bb的速度为：

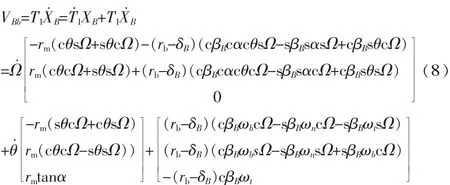
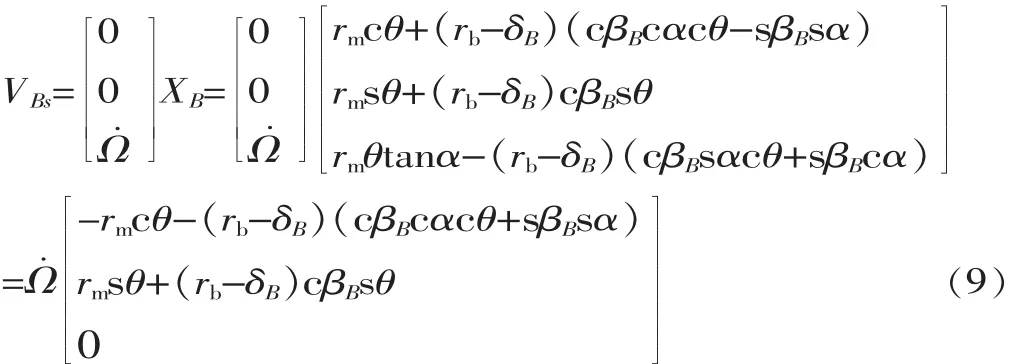
显然，式（8）和式（9）并不相等，因此，在接触点 B处丝杠和滚珠间必然存在相对运动。由于滚珠绕T坐标轴的旋转速度几乎为0，可以忽略不计。则接触点B处丝杠和滚珠间相对运动速度为：

其中：

同样，螺母和滚珠的接触点A处也存在相对运动，其相对运动速度为：

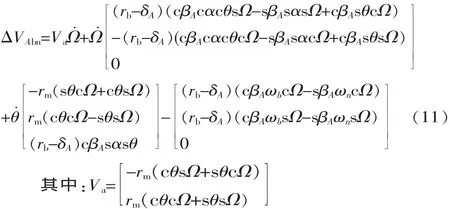
由式（10）、式（11）知，丝杠和螺母间存在速度偏差，速度偏差与接触角、滚珠半径、螺旋升角丝杠半径等相关。速度偏差的存在，使滚珠丝杠在传动过程中，工作台的运动不平稳，出现位置波动，不仅对动态定位精度有影响，还会加速滚珠丝杠的磨损，影响滚珠丝杠的寿命。因此，减小螺旋升角、增大接触角以及提高材料的弹性模量等，可以降低丝杠和螺母的速度波动，提高滚珠丝杠的运动平稳性。

2 滚珠丝杠副接触刚度

2.1 滚珠丝杠副接触变形

2.1.1 接触力分析

▲图3 滚珠丝杠-滚珠-螺母接触力分析

滚珠丝杠副的滚珠与螺母、丝杠的接触问题可以视为典型的滚动接触问题，利用赫兹接触理论进行分析。接触点中心位于NB平面，如图 3所示，在运动转换过程中，滚道中的滚珠承受4个外力，分别为与丝杠接触产生的接触变形力qA和摩擦力fA，与螺母接触产生的接触变形力qB和摩擦力fB。假设在NB平面内，滚珠与丝杠接触点处的摩擦角为φA，与螺母接触点处的摩擦角为φB，则滚珠所受外力在T、N和B方向的分力分别为：

对滚珠的运动过程进行分析，获得滚珠质量m在各方向的加速度，通过牛顿第二定律，获得滚珠在运动过程中的外力为：

假设与螺母固连的工作台上受一外力Fa，不考虑制造误差等影响，则外力Fa将被平均分配到滚道中的每一个滚珠体上，在滚珠与丝杠和螺母接触点处的受力平衡方程分别为：

式中：z为滚道中滚珠的个数。

2.1.2 接触变形分析

滚珠丝杠副滚珠与丝杠、螺母的接触情况可以视为球轴承接触情况并对其进行分析。滚动接触分析模型可以视为两个相互接触的半球体，如图4所示，由赫兹接触理论可知，在此情形下的接触区域形状为一椭圆。假设两个半球体分别受大小相等的外力P的作用，在同一个平面内，两个半球体通过接触点的主曲率和曲率半径与未受外部载荷时的主曲率与曲率半径相同，在XZ平面和YZ平面内的接触点处的相对曲率分别通过下式进行计算。

式中：rix、rjy分别为半球体i、j在XZ平面和YZ平面内的曲率半径。

相互接触两个半球形成的接触区的有效半径比γ和椭圆度κ为：

式中：a、b分别为椭圆形接触区域在XZ平面和YZ平面内的半径。

在滚珠丝杠副接触情形下，滚珠与滚道的接触为凸-凹的接触形式，接触区曲率和为：

▲图4 滚珠丝杠接触模型

按照赫兹接触理论［4］，接触变形δ与法向接触力P的关系为

已知 ζ、ξ、κ 的最优估计方程［5］，将式（14）及最优估计方程代入式（20），则变形与法向正压力Fa的关系为：

由式（15）可知，螺母与丝杠接触的法向接触力不仅与丝杠螺母接触的法向接触力相关，还与滚珠、丝杠的转动速度相关。

滚珠与螺母、丝杠接触产生的变形在丝杠轴向的投影为：

以作用力F与变形δz′的商定义为滚珠丝杠轴向接触刚度［6］：

则滚珠丝杠副的轴向接触刚度将是一与外部负载、丝杠及滚珠转速、接触角、螺旋升角及材料特性等相关的非线性参数。

2.2 接触刚度仿真

由式（21）可知，接触变形与滚珠丝杠副的螺旋升角α、滚珠与丝杠接触角βA、滚珠数量 z、曲率和R等结构参数相关，并受相互接触两结构的等效弹性模量E和等效泊松比γ的影响，变形随外部负载力的变化呈现出非线性变化。因此，滚珠丝杠副接触刚度将会因上述参数的变化而发生变化。为研究接触刚度特性，笔者对上述参数中螺旋升角α、接触角βA及负载变化导致的滚珠丝杠副接触刚度变化进行仿真分析。

2.2.1 负载对接触刚度的影响

对滚珠丝杠副接触刚度进行仿真实验，其具体参数见表1。由于螺母与滚珠间的接触变形与运行速度等相关，因此，此处仅考虑丝杠与滚珠接触来探讨接触刚度K与负载力F的关系。以MATLAB2008作为数值计算工具，以周期力 F=A［1+sin（ωft）］作为激励对其进行仿真计算，在此设定周期力周期ωf=20 Hz，幅值A=1 000 N，t为时间,s。仿真结果如图5所示。

由图5可知，所计算的滚珠丝杠副接触刚度幅值在108N/m量级，随外部载荷的增加，滚珠丝杠副的接触刚度将变大。在前半段刚度随力的增加幅度较大，在后半段增加幅度放缓。这是由于随着外部载荷的增加，接触变形变大，滚珠和丝杠（螺母）接触区域的面积也增大，增加的幅度随力的增加而逐渐放缓。因此，可以通过在丝杠和螺母间施加一定幅度的预紧力，以减小由于接触变形对滚珠丝杠运动精度带来的影响。

2.2.2 接触角和螺旋升角对变形的影响

由式（21）可知，滚珠丝杠副的弹性变形量与螺旋升角及接触角相关。在实际选择滚珠丝杠副时，为了实现高速传动，通常会选用较大导程的丝杠。螺旋升角与丝杠导程直接相关，因此忽略了导程对滚珠丝杠副运动特性的影响。另外，滚珠与丝杠和螺母的接触角极易受使用环境及安装状态的影响。基于以上考虑，针对接触角和螺旋升角对滚珠丝杠接触变形的影响进行分析。

表1 滚珠丝杠仿真模型结构参数

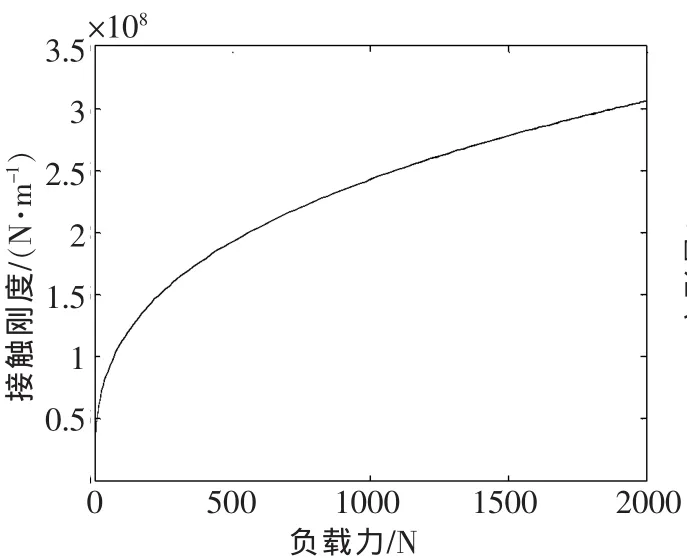
▲图5 滚珠丝杠接触刚度与负载力的关系图

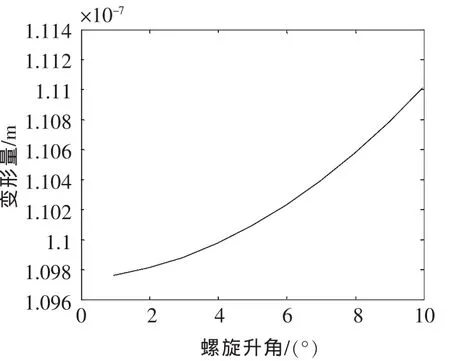
▲图6 螺旋升角与变形量的关系

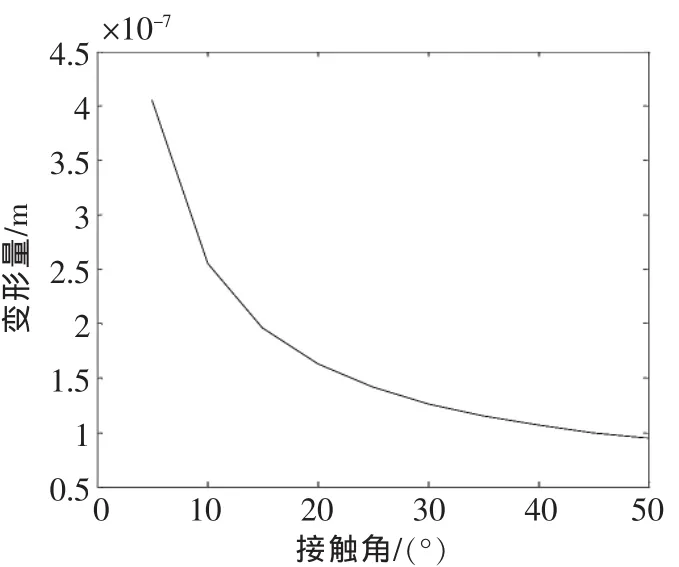
▲图7 接触角与变形量的关系

基于表1参数，以步长1°改变螺旋升角，得到的变形量与螺旋升角的关系如图6所示。丝杠一边变形量随螺旋升角的增大而增大。螺旋升角增大9°，变形量增加1.2×10-9m。由螺旋升角变化引起的变形量值较小，在实际选择滚珠丝杠时可以忽略。

以步长5°改变接触角得到变形量与接触角的关系如图7所示。随着接触角的增大，丝杠与滚珠的接触变形在0～30°范围内减小较快，在＞30°范围内减小放缓。接触角从5°增加到50°，接触变形量降低了3×10-7m。因此，在选型及安装过程中，选择滚珠丝杠副的接触角＞30°，可以明显降低接触变形。

3 结论

将丝杠、螺母、滚珠作为刚体，对其空间运动过程进行建模，分析了在动态传动过程中接触变形、接触角、螺旋升角、滚珠半径、丝杠半径、导程等参数会影响滚珠丝杠的传动精度。滚珠与螺母和丝杠接触点的速度偏差会影响丝杠运动平稳性。减小螺旋升角，增大接触角以及提高材料的弹性模量等，可以有效降低丝杠和螺母的速度波动，提高滚珠丝杠的运动平稳性。另外，可以通过在丝杠和螺母间施加一定幅度的预紧力，来减小由于接触变形对滚珠丝杠运动精度带来的影响。在选型及安装过程中，通过选择滚珠丝杠副的接触角＞30°，可以明显降低接触变形。

［1］ 牟世刚,冯显英.高速滚珠丝杠副动态特性分析［J］.湖南大学学报（自然科学版）,2011（12）：25-29.

［2］ Chin Chung Wei,Jen Fin Lin.Kinematic Analysis of the Ball Screw Mechanism Considering Variable Contact Angles and Elastic Deformations ［J］.Journal of Mechanical Design,2003，125（4）：717-733.

［3］ Yang T C,C S Lin.Identifying the Stiffness and Damping Parameters of a Linear Servomechanism ［J］.Mechanics Based Design of Structures and Machines,2004， 32 （3）：283-304.

［4］ Symens W,H Van Brussel， J Swevers.Gain-scheduling Control of Machine Tools With Varying Structural Flexibility［J］.CIRP Annals-Manufaturing Technology,2004，53（1）：321-324.

［5］ Frey S,A Dadalau ，A Verl.Expedient Modeling of Ball Screw Feed Drives ［J］.Production Engineering,2012（6）：205–211.

［6］ 吴南星,胡如夫,孙庆鸿.数控车床丝杠进给系统刚度对定位精度的影响［J］.中国工程科学,2004（9）：46-49.