蚁群算法中改进的蚂蚁选择城市概率公式

曹严清， 王 涛

（长春工业大学 计算机科学与工程学院，吉林 长春 130012）

0 引 言

20世纪50年代中期创立了仿生学，人们从生物进化的机理中受到启发，提出了解决复杂问题的优化方法，如遗传算法、免疫算法等。遗传算法是一种群体智能算法，其本身具有并行性和分布式特点。该算法是模拟蚂蚁寻找食物的过程，由意大利学者A.Colomi和M.Dorigo等人于1992年首先提出来的。TSP问题中的概率选择公式是蚂蚁选择下一城市的参考标准，标准蚁群算法中包含信息素和相邻城市间距离两个因素。标准蚁群算法由于信息素的积累，容易出现早熟停滞现象。文中针对早熟和停滞现象，在概率选择公式中加入了以历代最优解作为参考的启发式信息，削弱信息素在蚂蚁选择路径时的影响，扩展解空间，避免过早陷入局部最优。运用TSP问题，对改进蚁群算法与标准蚁群算法做对比，验证了算法的有效性［1－3］。

1 经典的蚁群算法

个体蚂蚁之间是通过信息素来传递信息的，进而相互合作来完成复杂的任务。蚂蚁在移动时能够留下信息素，并且蚂蚁在运动过程中能够感受到这种物质的强弱，以此作为引导自己运动的方向，蚂蚁会朝着这种物质浓度高的地方运动。大量蚂蚁的集体行为就表现为一种信息正反馈，某条路径走的蚂蚁越多，这条路径上的信息素浓度就越大，这条路径被别的蚂蚁选择的可能性就越大。蚂蚁个体就是靠这种简单的信息交流找到蚁穴与食物之间的最短路径，此过程没有总体指挥。蚁群算法通常用于TSP问题。

用蚁群算法处理TSP问题，有m只蚂蚁在图的相邻节点之间移动，通过合作来得到问题的解，每只蚂蚁在选择下一个节点时，由通向下一个节点的弧上的两类信息决定：其一是这条弧上的信息素浓度；其二是这条弧的长度。信息素有两种更新方式：一种是所有路径上的信息素都会以某种比例减少；另一种是被蚂蚁走过的某条边上的信息素浓度会增加。最初蚂蚁只是随机地选择路径，随着多代多只蚂蚁的探索，就会积累具有局部优势的启发式信息，根据启发式信息逐步达到最优解［4］。

建立禁忌表可以让蚂蚁不再访问走过的节点，蚂蚁通过信息素进行选择，当某些路径上的蚂蚁越多，路径上就会留下更多的信息素，蚂蚁选择这条路径的概率就会增加，就会进一步增加这条路径上的信息素浓度，路径上没有蚂蚁通过或只有较少的蚂蚁通过，路径上的信息素会因为蒸发而显得相对较少。蚂蚁的信息素更新，有从一个节点移动到另一个节点就更新信息素，也有一代蚂蚁构建出一条路径后才更新信息素的。

模拟蚂蚁的行为，引入以下记号：

m——蚂蚁的数量；

n——TSP问题中城市的数量；

dij——城市i和j之间的距离；

ηij——一边（i，j）的启发信息，反映由城市i到城市j的距离信息，在TSP中ηij＝1／dij；

τij——一边（i，j）上的信息素量；

个体蚂蚁的行为特征：

1）蚂蚁完成一次循环后，蚂蚁会在走过的路径上留下信息素。

2）蚂蚁选择城市，是根据路径上信息素浓度和城市间距离。

3）完成一次循环之前，蚂蚁不允许访问已被访问过的城市。

系统过程如下：

m只蚂蚁随机被分配到m个城市。各个路径上设置相等的初始信息素浓度值，设τij（0）＝τ0，τ0是信息素浓度初始值，可设为τ0＝m／cmn，m为蚂蚁数量，如果τ0太小，搜索将陷入较差的局部空间，τ0太大只有信息素蒸发到足够小时，蚂蚁释放的信息素才会发挥指引作用。

蚂蚁是随机选择下一个城市的，位于i城市的蚂蚁选择j城市依据如下概率公式

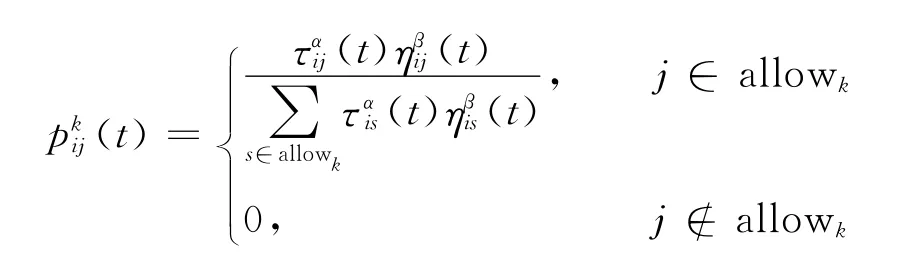
式中：τij——路径（i，j）的信息素浓度；

ηij——城 市 间 距 离 的 启 发 式 信 息，ηij＝1／dij；

α，β——两个启发式信息的参数，决定启发式信息对蚂蚁选择城市影响的程度；

allow——蚂蚁未访问城市的集合。

以上是个体蚂蚁的行为特征，要想得到局部最优解，需要多只蚂蚁多代寻找路径，一旦发现新的最短路径，就将此路径记录下来。

2 经典蚁群算法的不足之处

在标准蚁群算法中，由于信息素的积累，在算法初期就会得到局部最优解，在最优路径上的信息素浓度高于其他路径上的信息素浓度，蚂蚁选择路径时以此作为参考，就失去了探索解空间的能力，将会导致算法陷入局部最优［5］。此后的大部分时间都是对局部最优解的重复搜索。针对这些不足，学者们提出了一些改进算法。Stutzle和Hoos提出最大最小蚂蚁系统（MMAS）［6］，设置信息素的上下限，避免过早停滞［7］；最优最差蚁群系统（BWAS）对最优解增强，最差解减弱；基于排序的蚂蚁系统，对蚂蚁所走路径大小进行排序，并对路径赋予权重，路径长度较小的权重较大；还有通过增加路线来改善一些算法的不足，如：K－opt、Or－opt节线交换法［8］；引入变异机制；自适应改变信息素的挥发，自适应改变路径上的信息素［9］；相遇算法提高了蚂蚁遍历的质量。文中加入以历代最优解作为参考的启发式，可以拓展解空间，因为历代最优解的各条弧并不一定在此代信息素浓度高的路径上，削弱了信息素的影响，如果选择了信息素浓度不高的弧，较标准蚁群算法就扩展了解空间，避免过早的陷入局部最优［10－11］。

3 改进的蚁群算法

以上是经典的蚁群算法的个体蚂蚁选择城市的概率公式，为了兼顾历代最短路径搜索结果，将结果信息纳入启发式信息，历代结果中弧出现的次数作为启发式信息［12］。在传统的概率选择公式上加了一个启发式信息ωij，ωij（用公式编辑器）是在历代最短路径中（i，j）弧出现的次数，弧出现的次数多，对蚂蚁的选择有正向影响，在程序中用minTourRec［］［］这样的二维数组存储。新的概率选择公式如下：

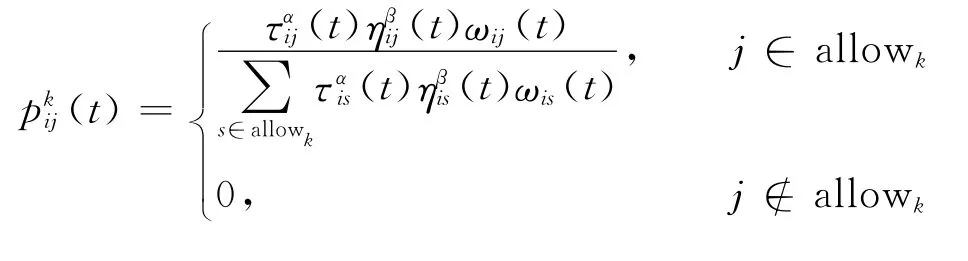
除了ωij，其余符号的意义均与上述标准蚁群算法符号的意义相同。

改进算法中的信息素增加，使用的是和标准蚁群算法一样的全局调整，公式如下：

Lk在本次循环中第k只蚂蚁所经过路径总长度，即完成一次循环后，才进行信息素的全局调整，Q为常数。

4 性能分析

从TSPLIB中选取TSP问题，用Java语言进行编程，对标准蚁群算法和改进的蚁群算法进行了大量的实验。实验中所用到的参数为α＝1.0，β＝2.0，τ0＝9.1，ρ＝0.5，Q＝1，迭代次数为2 000。

经典的蚁群算法与改进的蚁群算法，使用48个城市的att48的TSP问题做了5组对比，见表1。

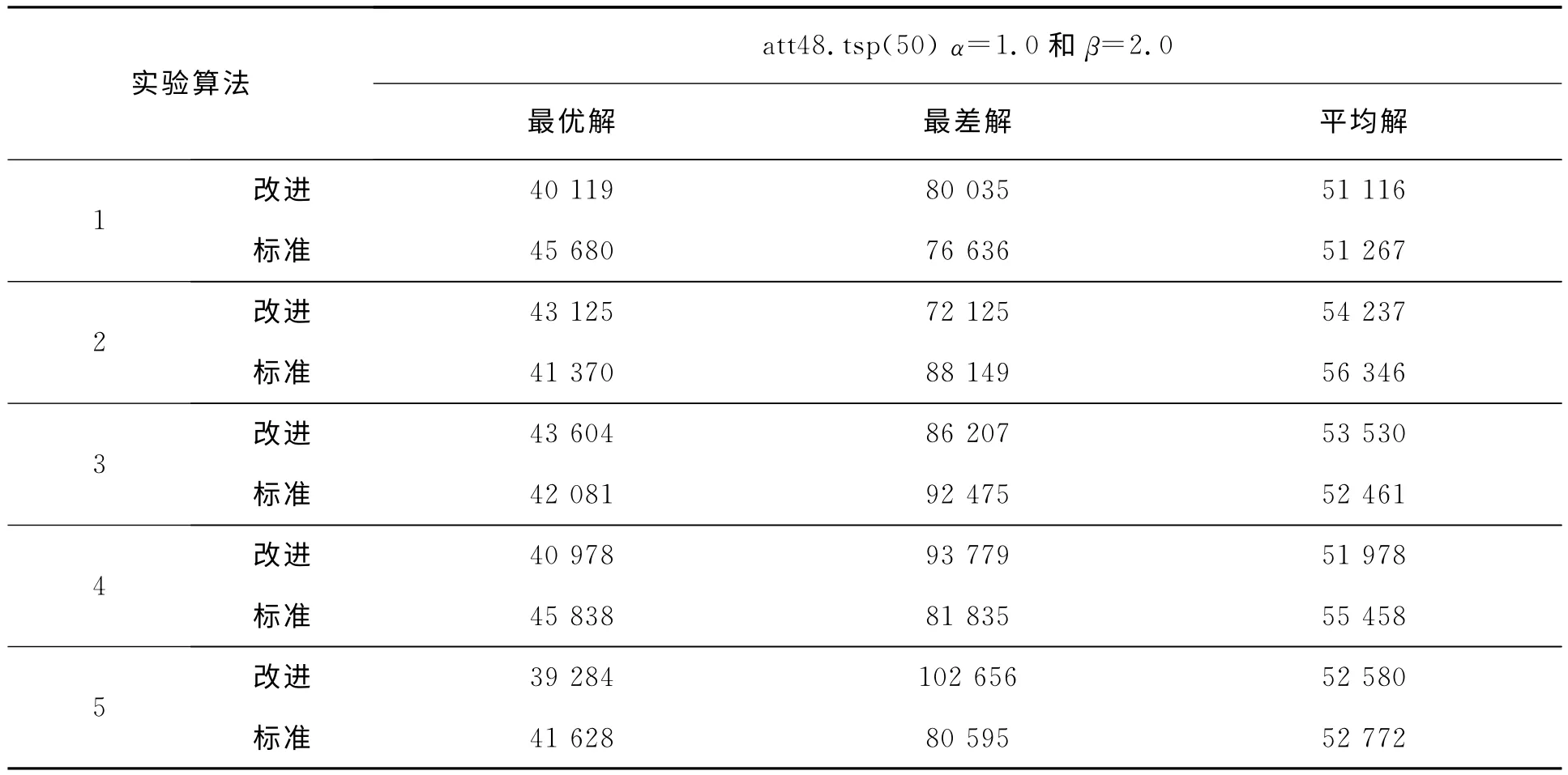
表1 标准蚁群算法与文中改进蚁群算法5组实验对比

每组两种算法各连续运行30次。在总共300次运行中，最优解是由第5组改进算法得到的，如图1～图5所示。

改进算法加入的启发式扩展了解空间，缓解了过早陷入局部最优，在第1组和第4组中，改进算法的一些解会明显地在传统算法主体解趋势之下（见图1和图4）。

在上述实验的基础上，又对不同的TSP问题对标准蚁群算法和改进蚁群算法进行了实验对比。选取了Berlin52，Eil51，Eil76，St70这4个TSP问题。4种TSP问题的算法中所用到的参数均为α＝1.0，β＝2.0，τ0＝9.1，ρ＝0.5，Q＝1。

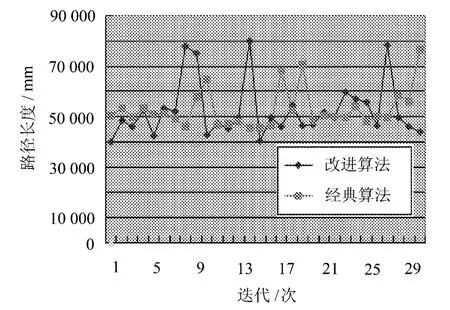
图1 第1组标准算法与改进算法各连续运行3 0次解的折线图

图2 第2组标准算法与改进算法各连续运行3 0次解的折线图

图3 第3组标准算法与改进算法各连续运行3 0次解的折线图

图4 第4组标准算法与改进算法各连续运行3 0次解的折线图

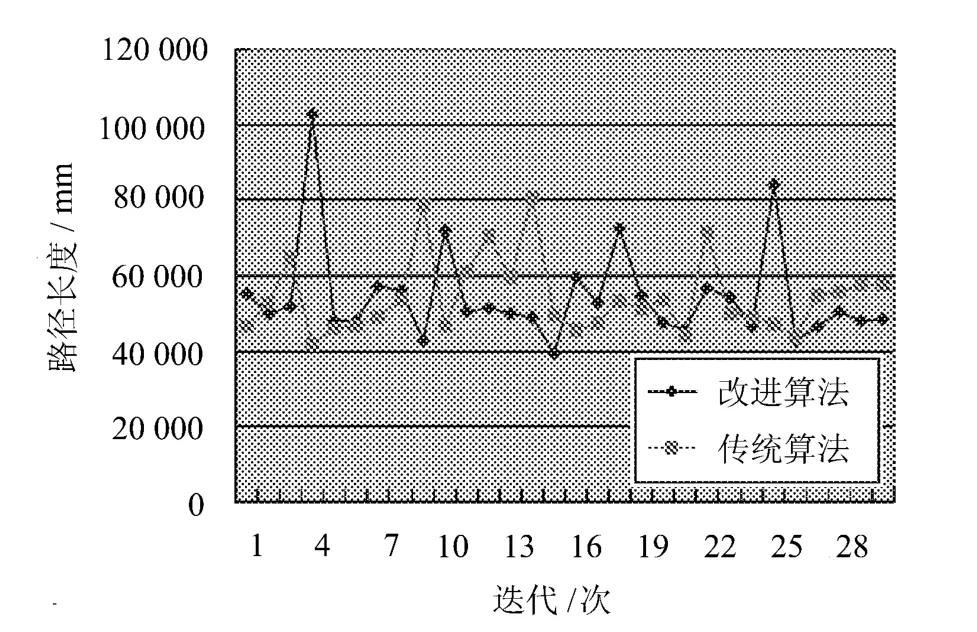
图5 第5组标准算法与改进算法各连续运行3 0次解的折线图

Berlin52，迭代次数均为2 000，Eil51的蚂蚁数量为50，标准和改进算法各连续运行30次。Eil76的蚂蚁数量为76，St70的蚂蚁数量为70，标准和改进各连续运行15次。实验结果见表2。

从表2中可以看出，改进蚁群算法的最优解均小于标准蚁群算法的最优解。Berlin52，Eil51，Eil76改进算法的平均解均小于标准算法的平均解，说明了改进算法的有效性。

5 结 语

提出了对蚁群算法的改进，把蚂蚁将要选择的下一节点与当前节点之间弧在历代最短路径中出现的次数作为蚂蚁选择下一节点的正向影响因素。避免蚂蚁过早的陷入局部最优解。

各种TSP问题实验结果表明了该方法的有效性。随着蚁群算法研究的深入，这种仿生算法将会得到更广泛的应用。

表2 标准蚁群算法与改进蚁群算法针对不同TSP问题的实验对比

［1］ M Dorigo，L M Gambardella.Ant colony system：a cooperative learning approach to the traveling salesman problem［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：53－66.

［2］ M Dorigo，G L M DiCaro.Gambardella Ant algorithms for discrete optimization［J］.Artificial Life，1999，80：130－172.

［3］ G DiCaro，M Dorigo.AntNet：Distributed stigmergetic control for communications networks［J］.Journal of Artifical Intelligence Research（JAIR），1998，102：312－365.

［4］ G DiCaro，F Ducatelle，L M Gambardella.AntHocNet：an ant－based hybrid routing algorithm for mobile ad hoc networks［C］／／Proceedings of Parallel Problem Solving from Nature（PPSN VIII），2004：143－150.

［5］ M Dorigo，T Stutzle.Ant colony optimization［M］.USA：MIT Press，2004.

［6］ S Thomas，H H Holger.MAX－MIN ant system［J］.Future Generation Computer Systems，2000，16（8）：889－914.

［7］ D Merkle，M Middendorf，Schmeck H.Ant colony optimization for resource－constrained project scheduling［J］.IEEE TransEvol Computer，2002，6（4）：333.

［8］ 夏亚梅，程渤，陈俊亮，等.基于改进蚁群算法的服务组合优化［J］.计算机学报，2012，35（2）：271－281.

［9］ 陈崚，章春芳.并行蚁群算法中的自适应交流策略［J］.软件学报，2007，18（3）：617－624.

［10］ 郑啸，罗军舟，宋爱波.基于Agent和蚁群算法的分布式服务发现［M］.软件学报，2010，21（8）：1795－1809.

［11］ 郭禾，程童，陈鑫，等.一种使用视觉反馈与行为记忆的蚁群优化算法［M］.软件学报，2011，22（9）：1994－2005.

［12］ 张良.约束满足问题求解启发式研究［D］：长春：吉林大学，2014.