发生的概率为定值时事件间的独立性分析

●谢鹏作 (玉门市第一中学 甘肃玉门 735211)



发生的概率为定值时事件间的独立性分析

●谢鹏作 (玉门市第一中学 甘肃玉门 735211)

在教学过程中,发现学生对事件独立性的理解存在误区,主要表现在2个方面：一是把条件概率中的相乘关系误认为是独立关系中的相乘关系;二是当2个事件发生的概率为定值时误认为是独立关系.面对第2个误区，笔者引用课堂实录阐明问题,愿给读者在教学中提供有用素材.

1 条件关系下概率为定值的事件独立性分析

组织学生学业水平考试复习之际,笔者在批阅《甘肃省普通高中学业水平考试大纲与解读(数学2013)》第60页21题时发现,学生的解答错误率为100%.在感慨万分的同时,觉得题目令人三思,经仔细探究,将题目带回课堂,与学生共讨做法,现将过程阐述如下.

1.1 题目及与学生解答相同的参考答案

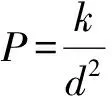
设第i次击中野兔为事件Ai,则

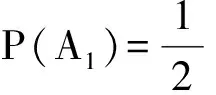
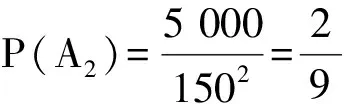
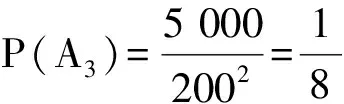
于是P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=

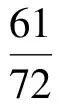
1.2 追问及引发的思索

师:如果第3次未击中,则猎人进行第4次射击,但距离已是250 m,……,如果第i次未击中,则猎人进行第i+1次射击,但距离已是50(i+1) m.已知此猎人命中的概率与距离的平方成反比，求5次内击中野兔的概率是多少(可以使用计算器)？

生:设第i次击中野兔为事件Ai,则

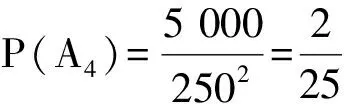
于是

P(A)=P(A1∪A2∪A3∪A4∪A5)=

P(A1)+P(A2)+P(A3)+P(A4)+P(A5)≈ 0.982 8.

师:6次内击中野兔的概率呢?

生:P(A)≈0.982 8+P(A6)≈1.023 6.

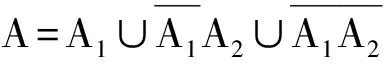
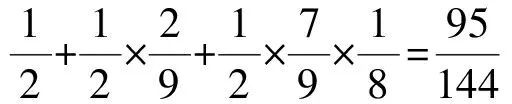
师:大家觉得该方法正确吗?

生:正确!

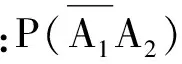
师:为什么独立呢?

师:请大家仔细思考,有不同的见解吗?

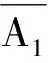
师(装作惊讶):大家觉得生1说得对不对?

(有少部分学生表示认同,大部分学生一言不发.)

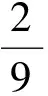
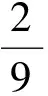
师:生1认为事件A1与A2是什么关系呢?

生1:事件A1与A2为条件关系.

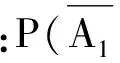
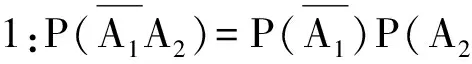
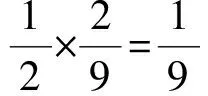
生(部分):不是一样么?

师:通过生1、生2的表达,可知

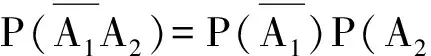
说明什么呢?请大家先阅读相关概念,再回答问题.

生:说明事件A1与A2既是条件关系又是独立关系.

生:都正确.

师:请大家想一想：怎样的2个事件既是条件关系又是独立关系呢?

生3:A发生的条件下,B才会发生,且A,B发生的概率为定值时,事件A,B既是条件关系又是独立关系.

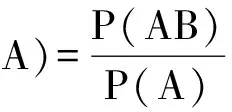
生5:3枪内击中野兔是指:第1枪击中,第1枪未击中时第2枪击中,第1,2枪都未击中时第3枪击中.从中可以看出,3枪内击中野兔有前后分步关系,即有前后分步关系且A,B发生的概率为定值时,事件A,B既是条件关系又是独立关系.

师:以上3位同学分别从不同角度表达了自己的认识,理解深刻到位,老师感到欣慰.已知A发生的条件下,B发生的概率P(B|A)与P(AB),P(A)有如下等量关系:

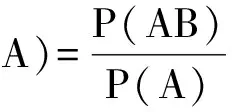
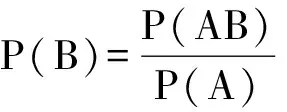
2 制约关系中概率为定值时事件的独立性分析

2.1 题目及解法

(《数学通讯(教师版)》问题208)

解法1 设甲,乙,丙,丁承包这项工程分别为事件A,B,C,D,且事件A,B,C,D两两互斥.因为

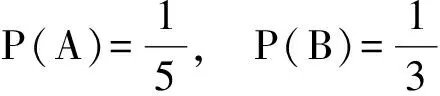
所以甲、乙、丙这3个公司中有1个公司承包的概率是

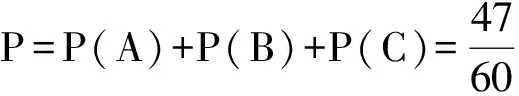
解法2 设甲、乙、丙、丁承包这项工程分别为事件A,B,C,D,且

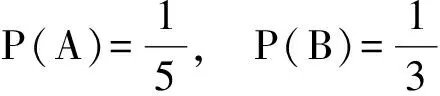
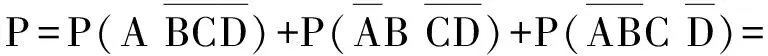
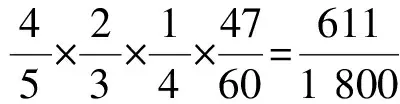
2 问题的深层分析

师:我们将2种解法展示于黑板,请大家认真思考,发表自己的看法.

2分钟后,学生无人发言.于是教师进行了调查：认同解法1的学生有26人,认同解法2的有14人,觉得2种解法都有道理的有11人.教师组织学生分组讨论,学生提出了以下问题.

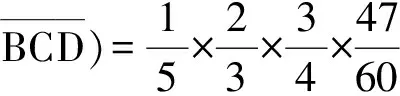
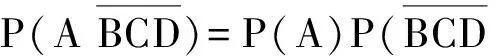
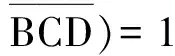
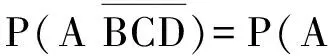
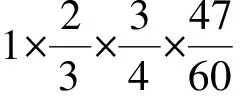
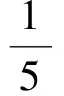
师:是啊,这能说明什么呢?

生(全体):错了呗!

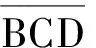
生11:因为事件B,C,D发生的概率为定值,所以事件B发生与否对事件C,D发生的概率没有影响,我认为事件B,C,D相互独立.

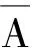
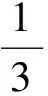
(此时,教室里一片寂静,大家陷入沉思之中.)

生12:从以上过程我们知道

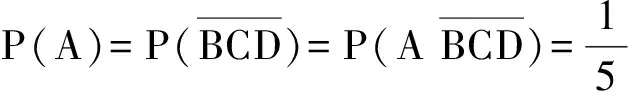
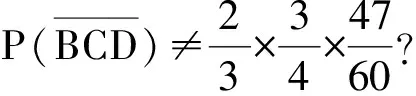
师:虽然事件A,B,C,D发生的概率为定值,但只能发生其中之一,事件A发生了,事件B,C,D就不发生了,即事件A,B,C,D之间有着相互制约的关系.也就是说事件A,B,C,D之间有相互制约关系时,即使有发生的概率为定值,但仍然不相互独立.

生:明白了.

师生相互交流，共同分析,探究问题实质与根源.在相互辨别中,厘清事件之间的关系,把握概率运算的关键,不论是事件的表达还是运算符号的确立,都要依据概念严格对待.有时,我们还要从问题的不同角度出发,相互印证,相互甄别,才能深入认识,加强对知识的理解.

有时将条件概率公式与独立事件都发生的概率公式混用,而结果却一样,就在于2者之间存在统一性.为什么概率为定值时,2个事件不相互独立？因为2者之间有制约关系,而不是条件或分步关系.教师通过案例深挖细究,与学生一起理解、体会、习得活动经验,不断提高解题能力.

[1] 邹国平.探究例题潜能,注重教学的“变”与“通”[J].中国数学教育：高中版，2011(1):88-89.