某型民机复合材料机翼下壁板开口补强及优化研究*

陈文俊，赵鲁春，李 军

(宜宾学院物理与电子工程学院，四川宜宾 644000)

0 引言

根据机翼结构设计要求，下壁板的层合板上开口或开口是不可避免的，如工艺施工、检查维修等。复材壁板开口，局部的纤维切断，引起结构的局部刚度和强度急剧下降，导致开口处在集中应力的作用下提前破坏;因此，壁板开口部位要进行补强设计［1］。

关于复合材料开口补强的问题，已有了一些研究。O'Neill［2］为了简化工艺，研究了顺序铺设的非对称补强问题，结果表明其强度只比相应的未补强层合板提高 5% ～12%。Pickett［3］研究了顺序铺设的对称补强问题，强度较未补强层合板提高了29% ～40%。显然，对称补强层合板强度明显提高。商霖［4］针对复合材料层合板开口的非对称补强进行了有限元分析，得出补强区域降低了孔边的应力集中，但并不能有效提高最先实效层的安全系数。J.H.Lee［5］使用了不同的材料，对开孔层合板进行胶接补强，发现使用铝补强较树脂、钢补强作用更为明显，尤其在压缩载荷作用下。寇长河、罗小东、郦正能等人［6－8］对圆形开口进行了非对称补强试验研究，认为复合材料非对称补强引起的偏弯效应十分明显，其应变比未补强板还要大。这些研究在实验或数值分析中对层合板开口补强进行了理论的研究，得出了一些结论。但没有与实践应用的层合板结构结合起来，利用有限元分析软件建立了机翼下壁的层合板结构，把开口补强与实践结构结合起来进行了研究。

1 机翼下壁板开口补强模型

某民用飞机采用双梁与单块混合的机翼，梁式机翼梁间跨度较大，便于利用机翼内部空间，也便于开口，开口后不会破坏传递弯矩和剪力的路线，仅为传递扭矩采取一些补强措施。

1.1 机翼下壁板材料及参数选择

机翼下壁板采用T300/QY8911，39根翼肋均为碳纤维复合材料T300/QY8911层压板结构。在层合板创建中，层合板铺层 ［±45/03/45/03/－45/90/0］s，单层厚度0.15 mm，如表1所列。

表1 T300/QY8911单向层压板性能

在保证使用和维护情况下，尽量肩上壁板开口数量，并使开口尺寸最小，一般检查油箱椭圆开口的长短轴最小尺寸为456 mm×254 mm。因此本模型选用的椭圆形开口的长短轴尺寸为640 mm×420 mm，。根据统计，最佳肋距在500 mm左右，对于小型飞机肋距约为300 mm，中型飞机为600 mm左右，大型飞机约为800 mm。因此本模型两根翼肋之间的距离选为700 mm。

1.2 机翼壁板补强方案

(1)未补强壁板 机翼下壁板考核处的开口为长圆孔，制孔时被切断的纤维量较多，刚度和强度下降幅度较大，因此必须进行补强设计，未补强的壁板见图1。

(2)壁板采用补片补强 由于开口纤维被切断，采用开口附近区域补片加固，可获得很好的补强效果，在允许情况下优先采用。一般补片直径是开口直径的1.5～2倍。补强片材料与母片材料相同，补片面积贴片够大，保证足够的层间剪切强度，补强处的壁板铺层是以均衡对称为主，结构形式见图2。

图1 下壁板开口情况

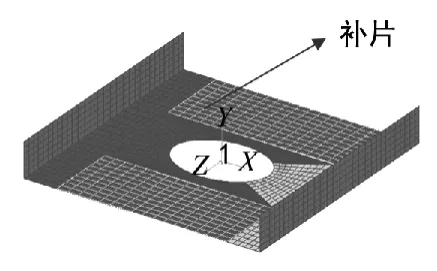
图2 下壁板补片补强

(3)壁板采用加强筋补强 加强筋补强方式是在未补强的壁板开口两边增加两个加强筋，其铺层顺序为［±45/03/45/90/－45/0］s，单层厚度 0.15 mm。为防止局部失稳，其补强方案结构形式如图3所示。

图3 下壁板加强筋补强

2 有限元模型网格划分

试件采用的节点单位剪力对角拉伸的加载方式模拟，有限元模型用MSC/PATRAN建立，通过MSC/NASTRAN计算，其中壁板的有限单元用二维壳单元来模拟。有三种不同方案的机翼下壁板有限元模型，分别是未补强壁板，补片补强壁板，加强筋补强壁板。如表2所列，为三种方案的节点数与单元数对比。

表2 三种补强方案节点与单元数对比

3 边界条件

在有限元计算模拟中，约束机翼壁板的一侧翼肋1、2、3、5自由度，在另侧翼肋出施加面内拉伸载荷和弯矩载荷(弯矩矢量方向平行于翼肋)，模拟外翼下壁板的主要受载形式。其载荷形式如图4所示。

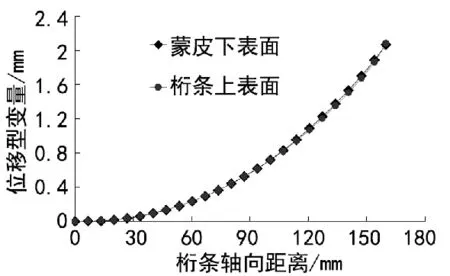
图4 下壁板载荷形式

4 有限元模型结果对比与分析

4.1 位移结果对比

有限元模型分析了局部机翼壁板受拉伸和弯矩作用下的变形情况，位移图如图5所示。

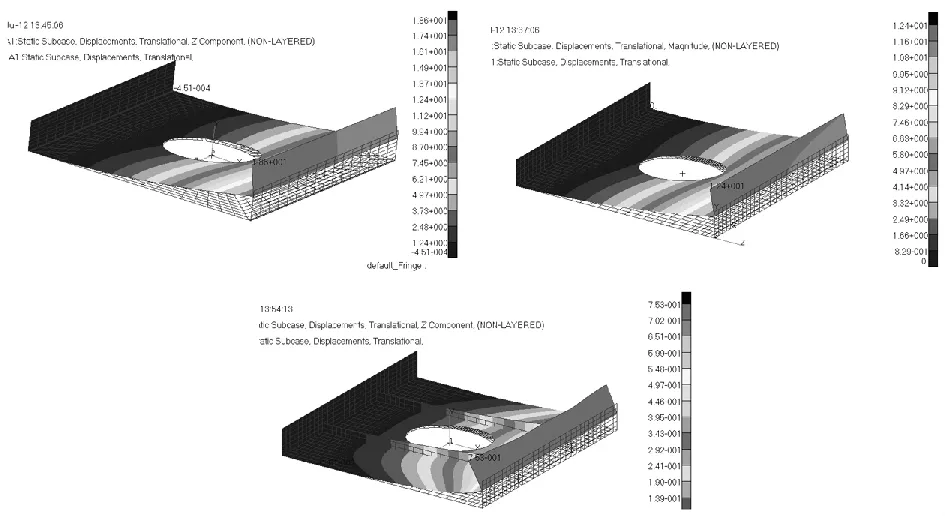
图5 三种下壁板模型位移对比图

由图5可以看出，对下壁板进行补强，能够很有效的减小最大位移，最大位移量对比如表3所列。

表3 三种方案最大位移 /mm

通过对比发现，补片式补强方案能在一定程度减小载荷作用下的最大位移，而加强筋补强可以将位移变化降为最低，仅仅为0.723 mm。仅为未补强壁板位移的4.04%，为补片补强位移的6.07%。因此，在相同的载荷作用下，加强筋补强能够最大程度减小位移。

4.2 应力分析

如表4所列为三种方案最大应力。

表4 三种方案最大应力 /MPa

如图6所示，通过对比最大应力发现，在应力集中位置方面，未补强与补片补强的最大应力都发生在开孔周围，而加强筋补强方案的孔周没有集中应力。从应力大小来讲，补片补强能够减小应力集中，比未补强壁板的应力减少了37%，而加强筋补强方案的应力比未补强壁板的应力降低了56%，补强的效果比未补强的效果提高很多。

图6 三种下壁板模型最大应力对比图

4.3 铺层角度对应力分布的影响

对比三种方案情况下各向铺层应力分布趋势图可知，未补强壁板在开口孔周围应力最大，补片补强壁板的应力在孔周围也有集中，单比未补强的应力要小。而加强筋补强的壁板在开口处没有应力集中，达到了很好的补强效果，如表5所列。

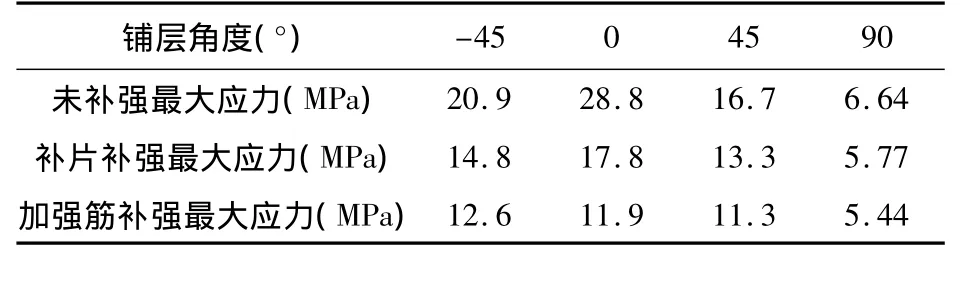
表5 不同铺层角度的最大应力值对比

分析表5可知，未补强层合板与补片补强层合板中0°铺层角度的单层板应力最大，因此在采用补片补强方案时，应尽量减少采用0°铺层。

从表5和图7可看出，对三种补强方案的各层最大应力及应力分布来看，加强筋补强方案比前两者的最大应力和应力分布均小很多。而对于各向铺层来看，在加强筋补强方案中，铺层方向为－45°的铺层应力最大，90°方向铺层应力最小，若采用加强筋补强方案应尽量减少－45°铺层，多采用90°方向铺层。

图7 三种方案的各层最大应力对比图

5 结论

本研究根据机翼典型结构在弯拉载荷下(未考虑扭转载荷)，依据经典层合板理论进行复合材料设计，对机翼蒙皮下壁板的开口进行补强进行静强度分析，并对补强结果进行对比。得出补片补强方案和加强筋补强方案均能减小位移和最大应力，而采用加强筋方案效果最好;若采用加强筋方案最大应力不再出现在0°铺层，而出现在－45°铺层;在设计机翼下壁板开口补强方案时应尽量选用加强筋补强方案，并尽量减少－45°方向的铺层，多采用90°方向铺层。

［1］ 飞机设计手册.结构设计［M］.第10分册.北京:航空工业出版社，2000.

［2］ O'Neill，G5.Asymmetric Reinforcement of a Quasi一 isotropic graphite［Z］.Epoxy Plate Containing a Circular Hole.AD －All9625M，F1985.

［3］ Pickett D H，Sillivan P.Analysis of Symmetric Reinforcement of Quasi－isotropic Graphite［Z］.Epoxy Plates with a Circular Cutout Under Uniaxial Tension Loading.AD－A139998MF，1988.

［4］ 商 霖.复合材料层合板开口的非对称补强研究［J］.导弹与航天运载技术，2009(4):40－43.

［5］ J.H.Lee.Strength of Composite Laminate with Reinforced Hole［J］.Journal of Composite Materials，1989(23):337.

［6］ 寇长河，汪彤，郦正能.复合材料层合板开口补强研究［J］.北京航空航天大学学报，1997(4):477－481.

［7］ Ali Al－Mansour，陈小全，寇长河.单面贴补修理后层合板的拉伸性能［J］.复合材料学报，2005，3(22):140－144.

［8］ 罗小东，寇长河，于卫东.复合材料层合结构开口的非对称补强研究［J］.航空学报，1994，15(12):1478－1481.