基于可靠性理论的海洋双井架分析*

2015-06-11张星，陈艳

机械研究与应用 2015年4期

张星，陈艳

(1.西安石油大学机械工程学院，陕西西安 710065;2.宝鸡石油机械有限责任公司，陕西宝鸡 721002)

0 引言

深水油气开发已成为海上油气开发的趋势。由于深水钻井作业的特性，海上钻井工程人员提出双井架钻井技术，主要特点是在平台井架上配备两台钻井系统［1］。由于深水作业时，井架承受很大的钻机重量和多种动态载荷，其中包括风激励产生的风载荷，海水波浪产生的波浪载荷等，因此为了保证钻井质量，对深海钻井双井架可靠性分析有极其重要的意义。笔者运用ANSYS软件对海洋双井架进行分析，得到井架在各种工况下的最大应力和结构临界载荷，利用可靠性理论分析计算了海洋钻井双井架可靠性，从而为井架的优化和评价提供理论依据。

1 井架建模与静力分析

1.1 模型简化与建立［2］

笔者选用Discovery Enterprise钻井船搭载的双井架作为参考，通过资料调研确定其主要的结构参数:井架底部开档 24.4×24.4 m;井架顶部开档 12.2×6.1 m;井架高度69 m;二层台高度 38.4 m;最大钩载:井架主体9 070 kN，辅助4 540 kN;游动系统结构:主体滑轮组7×8;辅助滑轮组5×6。井架具体各个杆件的型材及其具体截面尺寸参数均根据计算来确定。

海洋双井架结构复杂整体为三维桁架结构，杆件之间采用螺栓群连接，杆件不能绕连接点转动，即为刚性连接，自由度全部约束。建模时将井架主体的每一根杆件作为一个单元，杆件间的连接点作为节点。井架所带的扶梯、栏杆等附件，对井架的承载能力影响很小，可忽略不计。井架主要材料为H型16Mn钢，外形主要采用梯形，采用空间梁单元进行有限元分析。共划分152个节点，385个单元，所建立的有限元模型，如图1。

图1 双井架有限元模型

1.2 静力分析

井架内安装有两套钻机模块，井架内部的荷载也要分两部分进行计算。井架所受载荷包括恒载、工作载荷、风荷载、动力荷载。根据API Spec 4F及设计要求，主要对其进行4种工况的分析，每种工况有两种风载方向(背向吹风及侧向吹风)，共8种组合工况。具体工况如表1所列。

表1 工况的组合

通过有限元分析得到各个工况下双井架的应力和位移变化，最大应为90.2 MPa，小于16 MN钢的许用应力，满足安全要求。图2为严重钻井工况1的应力图和Y向的位移图，从图中可看出最大应力为90.2 MPa，方向与正方向相反，最大位移为35.97 mm。最大应力位于右侧的立柱上，由于两边加载不均匀，双井架各杆件受力不均匀;应力大小从上到下为先增大后减小，井架中部应力最大，由于风载和动载荷的作用，井架纵向位移变化较大。

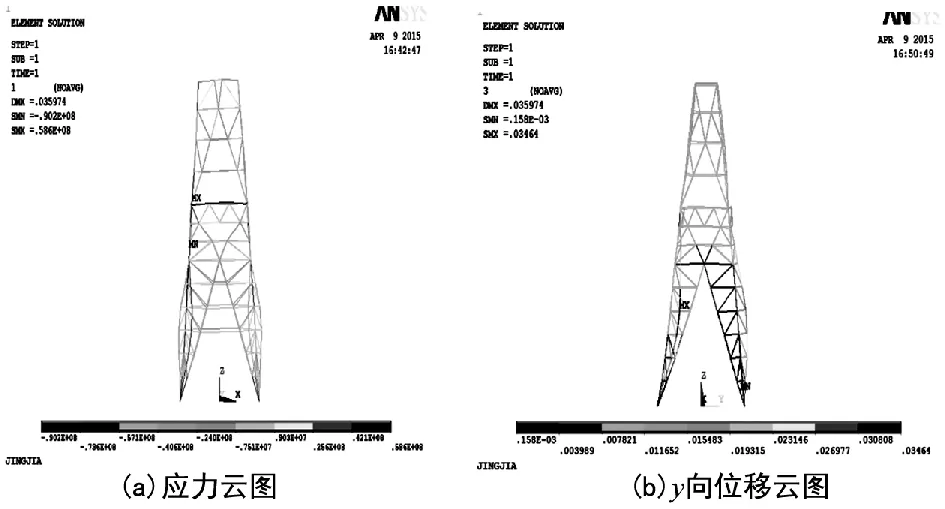
图2 严重钻井工况1的应力图和Y向的位移图

2 井架屈曲分析

屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷。线性屈曲分析主要步骤:设置预应力选执行一次静力分析，计算屈曲模态，进行扩展模态。采用前面建立的井架模型，井架施加初始荷载为1 kN，扩展四阶模态，分析结果如表2所列。

从表2可看出井架在各阶临界载荷逐渐增大，井架的一阶屈曲的临界载荷为18 581 kN，大于最大设计载荷，不会发生整体失稳。

表2 井架前四阶屈曲载荷

3 井架可靠性分析

双井架结构极限状态方程为:

Z=0时，双井架处于极限状态。

式中:R为井架的结构抗力，MPa;S为载荷效应，MPa。

结构的可靠性指标为:

式中:μZ和σZ分别为Z的均值和标准差，μS和σS分别为S的均值和标准差;μR和σR分别为R的均值和标准差。

结构的可靠度为:

式中:pr为可靠度;pf为失效概率;φ为标准正态分布函数。

3.1 井架的结构抗力和载荷效应的确定

钢材屈服强度、弹性模量、截面尺寸等与杆件抗力有关因素的不确定性均服从正态分布。由于构成抗力的各随机变量均服从正态分布，因此，由概率论的中心极限定理可以推出井架结构抗力近似服从对数正态分布［3－4］。

井架的工作载荷效应是标准正态分布，风载荷效应是对数极值I型分布，波浪载荷也呈对数极值I型分布，根据中心极限定理可知，井架整体载荷效应为对数极值I型分布。

3.2 结构可靠性指标的计算

将不服从正态分布的随机变量Xi等效为正态随机变量Xi'，对其进行当量正态化。当量正态化的条件是，在验算点处使非正态分布的随机变量Xi的概率分布函数值与当量正态随机变量Xi'的概率分布函数值相等，Xi的概率密度函数值与Xi'的概率密度函数值相等，用公式表示为:

结构功能函数为Z=R－S=R'－S'，从而得可靠指标的表达式:

方向余弦

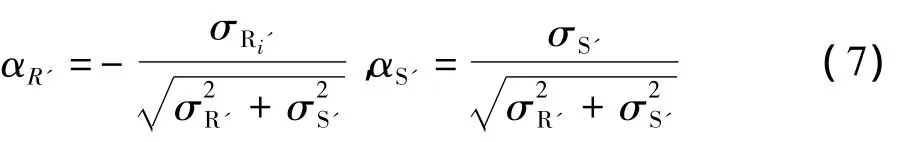
验算点的坐标为:

3.3 井架整体可靠性分析

根据统计资料得l6 Mn钢的抗力均值为:μR=345，变异系数δR=0.123，井架载荷效应主要分析井架承受最大载荷时严重钻井工况下的可靠性，若此工况符合规范要求即在承受最大载荷效应的情况下若井架的可靠性指标符合规范要求，则其他工况情况下均满足可靠性的要求，井架载荷效应根据数理统计方法求得均值 μS=62.85，方差 σS=45.2934，变异系数δS=0.164。迭代计算结果见表3。

第三次迭代与第四次迭代计算的可靠性指标结果已经相同，即β=5.2835，故停止迭代。所求可靠性指标大于《钢结构规范》中规定的3.7，可见结构安全可靠。将验算点坐标代入功能函数，Z=R－S=R'－S'=172.2357－172.2357=0，则结构的失效概率为 Pf=φ(－β)= φ(－5.2835)=10－6。