基于ARM的移动机器人路径规划控制算法研究*

李金彦

(宁夏工商职业技术学院机电工程系，宁夏银川 750021)

0 引言

移动机器人路径规划是人工智能与机器人学相结合的一个重要研究课题，其任务就是根据环境状态和工作信息在起始点和目标点之间规划出一条平滑路径。路径规划满足始于起始终于目标，安全避障，最快到达［1－3］三方面内容。传统的人工势场算法的结构相对简单，收敛性优越，便于底层的实时控制，规划出的路径比较平滑并且安全，尤其适合简单静态环境下的路径规划。但是，传统算法只是局部路径规划方法，存在局部极小值，在复杂动态环境中，极易造成移动机器人死锁现象:在障碍物和目标点接近时，机器人难以到达目标点;势场角度不易控制，机器人在障碍物前震荡等现象;在多障碍物紧密分布的情况下，机器人会在障碍物形成的狭窄通道中摆动［4－5］。

本文以机器人路径规划算法和具体策略为研究对象。采用二值图像的数学形态学的方法，利用膨胀运算和腐蚀运算两种对偶的基本变换算子，将离散的障碍物个体融合为完整的障碍物体，建立环境状态数学模型;对机器人工作空间进行全域搜索，寻求逃离局部最小点的运动方向;对算法实现采用PC与ARM控制模式，PC主要处理二值图像状态中膨胀和腐蚀操作并采集移动机器人实时坐标位置，这是基础控制层;ARM针对移动机器人自身携带距离传感器信息进行实时处理，设计移动路径，这是行为控制层设计。

1 人工势场法数学模型

人工势场法将机器人在周围环境中的运动，设计成一种抽象的人造引力场中的运动，目标点对移动机器人产生“引力”，而障碍物对移动机器人产生“斥力”，最后通过求合力来控制移动机器人的运动。

设机器人在空间中的位置为X=［x，y］T，机器人与目标点引力场函数为:

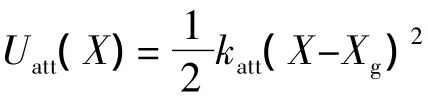
上述引力场对机器人产生的引力势能的负梯度为:

式中:katt为正比例常数因子;X为机器人当前在运动空间的位置［x，y］T;Xg为目标点在空间的位置［xg，yg］T，|X－Xg|为机器人当前位置与目标点的距离。可以看出，引力随机器人与目标点距离变小而线性减小并最终趋于零。

障碍物i对机器人产生的斥力场函数为:Ureps(Xi)=

上述斥力场对机器人产生的斥力势能的负梯度为:Freps(Xi)=－▽Ureps(Xi)

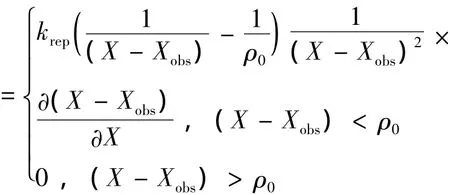
式中:krep为比例因子;Xobs为障碍物在运动空间中的位置;X－Xobs为障碍物与机器人的作用距离;ρ0为斥力阈值距离，距离超过ρ0，斥力可忽略不计，斥力场随着移动机器人与目标点距离的减少而减少，保持引力场始终大于斥力场。

所以机器人在运动空间中的合势场和合力分别为:

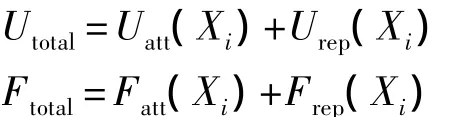
合势场与合力决定了机器人的运动，机器人在合势场的作用下，从高势场位置逐步向低势场位置运动，由于目标点被设计为合势场的全局极小点，理想状态下，机器人能够最终到达并止步于目标点。然而，在复杂环境下，多个障碍物会造成目标点以外的区域也存在极小点，因此导致机器人可能无法到达预定目标，从而产生死锁，如图1所示。

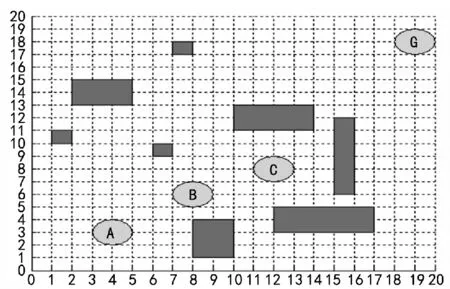
图1 机器人人工势场法“死锁示意图”

机器人从起始点(4，3)要到达目标点(19，18)，从A到B区域，主要受到目标点引力场和(8，1)处障碍物的斥力场，从B到C区域，各障碍物合力作用，在引力场作用下，移动机器人运动方向指向G点，但障碍物合围造成无法通过障碍，从而在C区域持续震荡，无法到达目标点。

2 改进的路径规划算法过程

针对机器人在障碍物前持续震荡并停止不前，对人工势场法算法进行改进，分为全局二维图像的处理和空白路径搜索法两方面。

2.1 全局二维图像的处理

对二维图像全局处理，是建立在上位机对静态环境已知的基础上，平面结构元素由0或1矩阵形式表现。结构元素原点和终点表现静态环境大小，而值为1的点，是需要处理的障碍物点［6－7］。采用数学形态学方法，利用膨胀和腐蚀两种对偶变换，将离散障碍物点融合为完整背景图像，用于对移动机器人运动路径的全局规划。

膨胀是用矩阵算子依次扫描每一个像素点，用矩阵中结构元素和覆盖的区域做“与”操作，如果结果全部为0，则该像素点为0;若为1，则二值图像该像素点为1。腐蚀是与膨胀运算对偶，选用不同矩阵算子扫描处理每个像素点，用矩阵中结构元素和覆盖的区域做“与”操作，若结果全部为1，则该像素点为1;若为0，则二值图像该像素点为1。膨胀和腐蚀处理都需要考虑到移动机器人的具体形态。障碍物较小，机器人可以自由轻松通过时，该障碍物可以作为噪声点进行处理;若两障碍物相邻，可以考虑融合在一起，更好规划移动机器人路径。

笔者选取3×3膨胀算子和腐蚀算子为:

分别对图像局部融合和去噪，图2为全局静态环境通过算子处理后状态。

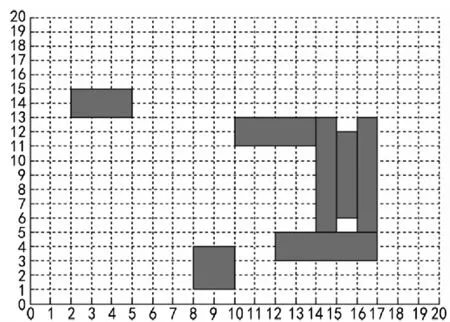
图2 算子处理后状态

2.2 空白路径搜索法

当移动机器人底层程序检测到自身陷入局部极小点后，停止运动，传送机器人环境数据，等待上位机指令。上位机根据移动机器人位置和静态环境信息，设定虚拟目标点。移动机器人启动搜索程序，通过旋转角度，改变原有运动方向，逃离局部极小值。

如图3所示，移动机器人沿1方向运动时处于死锁状态，有几个已知量:

(1)移动机器人本体半径为r，旋转半径为R，有n个距离传感器均匀分布于圆周。

(2)当前运动速度v和运动方向已知。

(3)L为启动空白搜索程序的阈值，是一个与v相关函数，根据ARM程序采样周期T，选择L=2.5×vT。此刻第i个距离传感器正对B障碍物，与i号传感器相邻传感器(顺时针方向)为，i+1，…，n，逆时针为i－1，…，1。逆时针检测到障碍物的传感器个数少于顺时针方向，确定机器人旋转方向为逆时针。旋转角度 θ≥ arccos(R/S)，S=|X－Xa|=，其中(x，y)为移动机器人在上位机静态环境中的坐标，(xa，ya)是障碍物A的位置。算法为:

θj=(i－j) 2 π/n，j≤i，j为程序中递增量。

图3 空白路径搜索

3 路径规划算法实现方案

3.1 硬件系统

图4为机器人硬件系统。

图4 机器人硬件系统

硬件系统采用ARM+PC模式，ARM是32位处理器，速度快，功耗低，集成度高，功能强大，因此ARM非常适用于移动机器人行为控制层;PC机系统决策力强，通信良好，易于扩展，作为基础决策层处理器;移动机器人运动底盘采用双轮差速驱动，配合2个万向轮，可原地转向、速度快、运动灵活，结构简单可靠，作为平台安装硬件电路和部件，路径规划硬件系统如图4。

3.2 路径规划的算法流程图

上位机和下位机算法流程如图5所示。

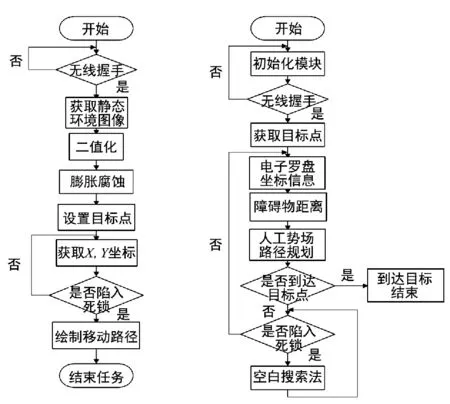
图5 上位机合下位机算法流程图

4 仿真实验及结论

为了检验机器人对于不同环境的适应能力，笔者考虑了如图1所示的复杂环境，该环境为20 m×20 m的平面区域，包含密集障碍物、狭窄过道和无障碍环境3种不同类型的区域。通过对复杂环境进行二值化处理和空白搜索，建立复杂环境数学模型，选择合理的初始化参数，得到仿真结果如图6所示。仿真结果表明，当目标点在障碍物范围内时，并且存在局部最小点时，使用改进的人工势场法，机器人能安全、快速到达目标点，如表1为初始化参数表。

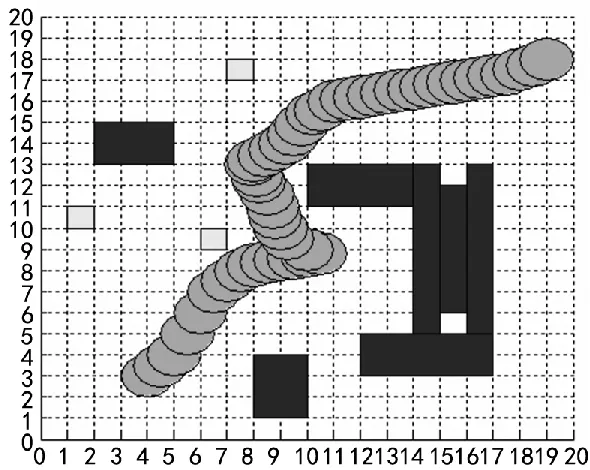
图6 仿真结果

表1 初始化参数表

5 结论

针对人工势场法在移动机器人路径规划中存在的“死锁”现象，建立了改进的人工势场数学模型，以PC机为决策层，以ARM处理器为控制层，采用上位机和下位机协调决策的方式，在原人工势场算法陷入极小值的状态下添加了“空白搜索法”，移动机器人很快解除“死锁”。通过仿真实验可知，以改进的人工势场法为机器人路径规划具有一定的适用性，该算法不但适用于单个障碍物进行避障，而且能实现多个障碍物构成的复杂环境，特别是连续C型障碍物环境下的避障动作，使得机器人继续前行从而安全快速到达目标地点。

［1］ CraigJ J.Introduction to Robotics:Mechanics and Control［M］.Second edition.Addison Wesley，2009.

［2］ Zhang B，Chen W M，Fei M R.An Optimized Method for Path Planning Based on Artificial Potential Field［C］.Jinan:ISDA，2006:35－39.

［3］ 高绪祥，刘 静，赵晓辉.具有越障和避障功能的小型移动机器人设计［J］.机械研究与应用，2010，23(4):71－73.

［4］ 戴 博，肖晓明，蔡自兴.移动机器人路径规划技术的研究现状与展望［J］.控制工程，2005，12(3):198－202.

［5］ 沈文君.基于改进人工势场法的机器人路径规划算法研究［D］.广州:暨南大学，2009.

［6］ 殷 路，尹怡欣.基于动态人工势场法的路径规划仿真研究［J］.系统仿真学报，2009，21(11):3325－3329.

［7］ 黄炳强，曹广益.基于模糊人工势场的移动机器人路径规划［J］.上海理工大学学报，2006，28(4):347－350.