离心式叶轮的概率失效分析*

张 昭，田 宇，张元良，张洪武

(1.大连理工大学运载工程与力学学部工业装备结构分析国家重点实验室工程力学系，辽宁大连 116024;2.大连理工大学机械工程与材料能源学部机械工程学院，辽宁大连 116024)

离心式叶轮的概率失效分析*

张 昭1，田 宇1，张元良2，张洪武1

(1.大连理工大学运载工程与力学学部工业装备结构分析国家重点实验室工程力学系，辽宁大连 116024;2.大连理工大学机械工程与材料能源学部机械工程学院，辽宁大连 116024)

以概率论和断裂力学为基础，考虑参数的不确定性和随机性，应用蒙特卡洛方法对再制造叶轮的疲劳寿命进行分析。结果表明，采用蒙特卡洛方法进行的一定可靠度和置信度下的寿命预测反映了参数的不确定性，较传统的断裂力学计算结果更安全;初始裂纹尺寸、断裂韧性、变异系数、气动载荷对疲劳扩展寿命的影响较大;将概率断裂力学应用于叶轮的疲劳寿命预测中，为相关叶轮的设计、检修提供了参考。

概率断裂力学;叶轮;蒙特卡洛法;疲劳寿命

0 引言

离心压缩机被广泛地应用于石油、能源电力、化工等众多领域中，具有很高的回收利用价值和再制造潜力［1］。随着国家可持续发展战略的推进，再制造压缩机的研究越来越受到关注。再制造叶轮是再制造压缩机的核心部件，再制造后的叶轮能否满足新的生命周期、能否有足够的服役安全性能是叶轮再制造的关键［2］。因此，再制造叶轮服役寿命预测具有迫切性和现实意义。

对叶轮的疲劳分析，国内外的学者们做了大量的研究。Li［3］等运用有限元方法和计算流体动力学方法预测轴流式叶轮叶片的疲劳寿命，提出了气动载荷和离心力载荷相结合的方法;Shokrieh［4］等预测风力涡轮机叶片的寿命，结果表明累积疲劳损伤模型和随机方法能够模拟风力涡轮机叶片的疲劳损伤过程;Chu［5］等对材料为FV520B的离心压缩机叶轮进行了失效分析，提出了适应服役环境的改进措施;Kim［6］等研究了蒸汽机叶轮叶片失效的原因，得出叶轮失效是由材料缺陷和超速加载引起的;刘明霞［7］等采用金相检测手段检测失效叶轮的焊接接头并模拟计算，结果表明应力集中加速了裂纹的扩展及失稳，造成产品的结构失效;Chávez［8］等以哥伦比亚的一个水电站用叶轮为背景，对叶轮进行了失效分析，结果表明材料存在初始缺陷，在焊接残余应力和离心力的共同作用下发生疲劳失效;Nie［9］等对失效的离心压缩机焊接叶轮进行了分析，提出了提高叶轮可靠性的措施;Ejaz［10］等对离心叶轮进行了失效分析，发现叶片根部的裂纹在高周疲劳下传播导致叶轮失效。目前，对叶轮的疲劳失效分析已有大量有意义的工作，大部分是基于传统的断裂力学理论或试验方法，然而在叶轮的不同部位，内部损伤具有不同的尺寸，并承受不同的载荷，因此，有必要采用概率统计的方法展开对叶轮的失效分析。

Monte Carlo方法是通过对随机变量函数的概率模拟、统计试验或抽样，求解不同问题的近似数值解的方法，它被广泛地应用于PFM模型中。Abu-Elanien［11］和 Liu［12］等分别运用 M-C 方法对结构进行疲劳寿命预测和失效分析，均取得了与实验数据一致的数值分析结果，验证了M-C方法的可靠性。因此，本文结合概率断裂力学，采用M-C方法，考虑参数的不确定性和随机性，预测叶轮在一定可靠度和置信度下的疲劳寿命，并讨论不同因素对疲劳寿命的影响。

1 模型描述及基本理论

离心式叶轮有限元模型及网格划分见图1。叶轮是旋转对称结构，模型共18个叶片，轮盘直径160 mm，轴孔直径19.5 mm，共划分27 498个单元，45 703个节点，自由度数为137 109。叶轮材料选用40CrNiMoA钢，材料参数见表1。

图1 叶轮有限元分析模型

表1 40CrNiMoA钢的材料参数［13］

等效应力的表达式为:

式中:“:”表示张量的双点积。

当坐标轴转换时，同一点的各应力分量如式(2)所示［14］:

式中:ni'i的下标 i'=1'，2'，3'对应于新坐标 x'，y'，z'(即 x1'，x2'，x3');其下标 i=1，2，3 对应于老坐标 x，y，z(即 x1，x2，x3)。当坐标轴转换时，应力分量遵循二阶张量的变换规律，虽然转轴后各应力分量都改变了，但其分量作为一个“整体”，所描绘的一点的应力状态是不变的。

等寿命条件下的σa-σm关系可以表达为Goodman 直线方程［15］:

式中:σa为循环应力幅;σm为平均应力;σ-1为疲劳极限;σu为高强脆性材料的极限抗拉强度或延性材料的屈服强度。此关系式简单，且在给定寿命下，由此做出的σa-σm关系估计式偏于保守，故在工程实际中常用。

预测疲劳裂纹扩展寿命有多种方法，其中最简单、应用最广泛的是Paris［16］公式，其表达式为:

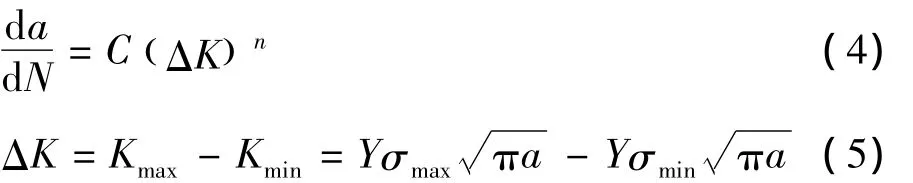
则疲劳扩展寿命为:

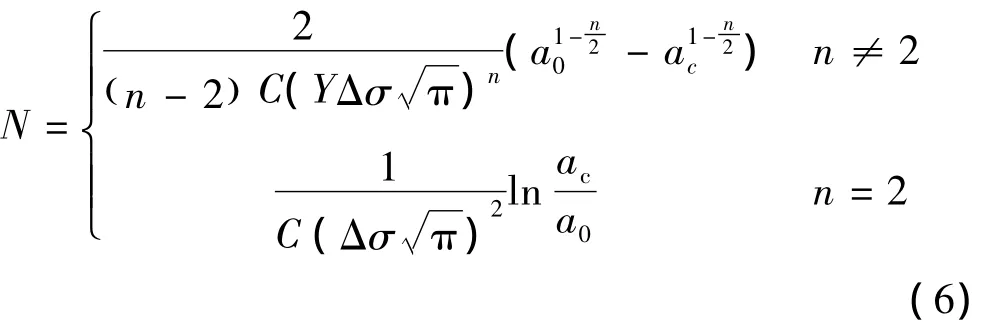
式中:C、n为材料常数;ΔK为应力强度因子幅度;Y为几何形状因子;Δσ为应力变化范围;a0为初始裂纹尺寸;ac为临界裂纹尺寸。

初始裂纹尺寸a0、应力变化范围Δσ及材料常数C均服从对数正态分布［17］，由式(6)可知疲劳寿命N也服从对数正态分布，即X=ln N是服从正态分布的。正态分布和对数正态分布参数的转换关系如下:

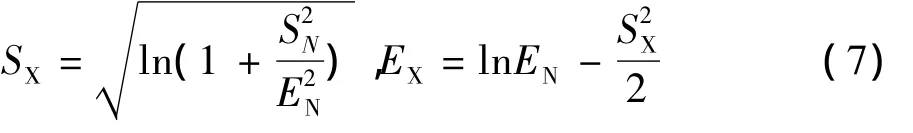
则可靠度为p时的对数疲劳寿命的计算公式为:

如果考虑置信度，则可靠度为p、置信度为r时的对数疲劳寿命的计算公式为:

式中:E、S分别为相应变量的均值和标准差，up为与可靠度p对应的标准正态偏量，k为单侧容限因数。

如图2为Monte Carlo模拟流程图。

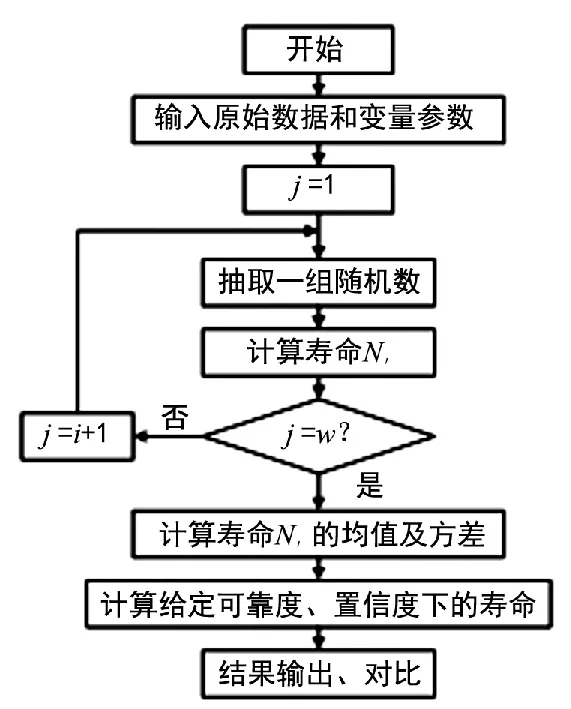
图2 Monte Carlo模拟流程图

应用M-C方法预测叶轮的疲劳扩展寿命，先按照Paris公式，对各随机变量每次抽取一个随机数，得到一个Ni，模拟w次，然后计算所得寿命的均值及标准差，最后得到一定可靠度和置信度下的疲劳寿命。

2 结果分析

Ⅰ型裂纹表面与受力方向垂直，所以需要转换坐标轴的方向求得与裂纹表面方向垂直的拉应力。图3为坐标轴转换前后等效应力的对比图，转轴前的等效应力与转轴后的等效应力吻合良好，验证了数值模拟的真实性和有效性。

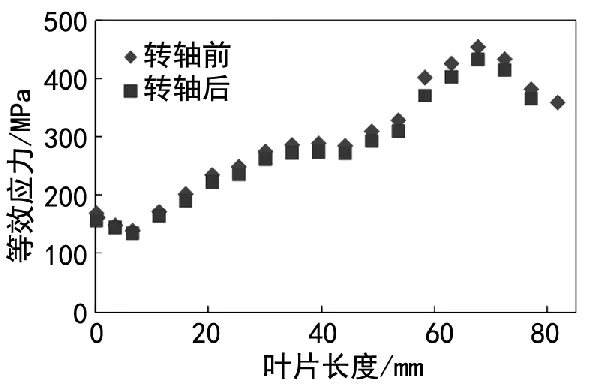
图3 等效应力对比图

叶轮的转速为m=53 075 r/min，有限元计算分析表明，叶轮稳定工作状态下，叶片前缘根部的拉应力σ=86.7044 MPa。叶轮在正常工作时受离心惯性力载荷和气动载荷的共同作用，离心惯性力载荷是不随时间变化的常值，而气动载荷是随时间变化的周期性载荷，因此气动载荷是引起叶轮产生交变应力促使叶轮发生疲劳破坏的根本原因。基于此，参考文献［3］，在叶片表面施加σd=0.04 MPa的面力模拟气动载荷，叶片前缘根部的拉应力σ=0.6528 MPa，根据式(3)，应力比R=-1时的应力幅σa(R=-1)=0.6907 MPa，则应力变化范围 Δσ=1.3815 MPa。工程中的变异系数 C.V 一般为 0.03 ～0.1［18］，笔者从最不利出发，取 C.V=0.1，具体统计参数见表2。

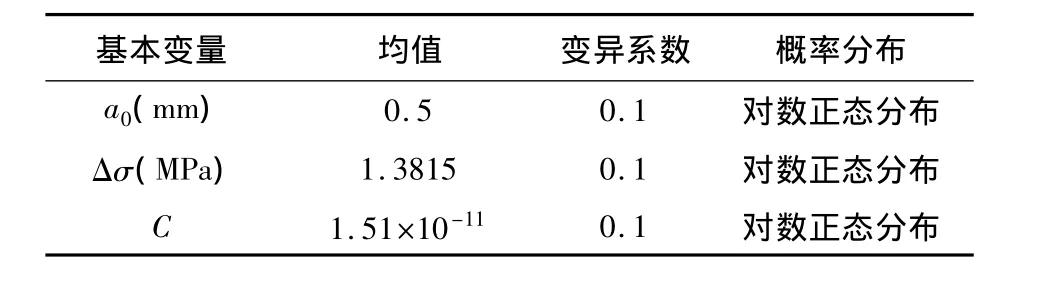
表2 随机变量及其统计特性

2.1 Monte Carlo方法与确定性方法的对比

分别运用确定性方法和M-C方法预测叶轮的疲劳寿命，结果见图4。由图可知，随着初始裂纹尺寸的增加，疲劳寿命逐渐减小，初始裂纹尺寸对疲劳寿命的影响较大。由表3可知，相同的初始裂纹尺寸下，理论计算和M-C方法求得的疲劳寿命误差均在5%左右，验证了M-C法求解疲劳寿命的准确性与可行性。

为了使预测出的安全寿命不超过其真值，需要考虑可靠度和置信度的影响，如图5所示。当a0=0.2 mm时，理论计算 N=1.357×1011次，程序计算 p=0.999 时的 Np=6.021×1010次，p=0.999、r=0.9 时的Npr=5.657×1010次;当 a0=0.5 mm 时，理论计算 N=9.912×1010次，程序计算 p=0.999 时的 Np=4.396×1010次，p=0.999、r=0.9 时的 Npr=4.131×1010次。出现偏差的主要原因是正常工况下叶轮叶片所受的载荷是波动的，初始裂纹尺寸a0、应力变化范围Δσ、材料常数C等都存在着随机性和不确定性，所以应用Monte Carlo法抽样求得的结果，更符合实际情况。相同的应力幅值下，随着初始裂纹尺寸的增加，疲劳寿命逐渐减小;相同的初始裂纹尺寸下，随着可靠度的增加，疲劳寿命降低，此规律分别与文献［19］、［20］吻合，说明本文模拟方法的有效性。

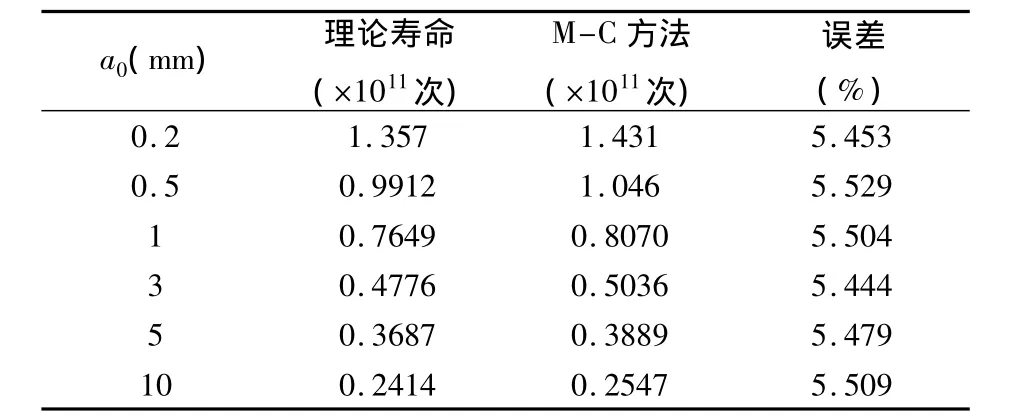
表3 寿命对比

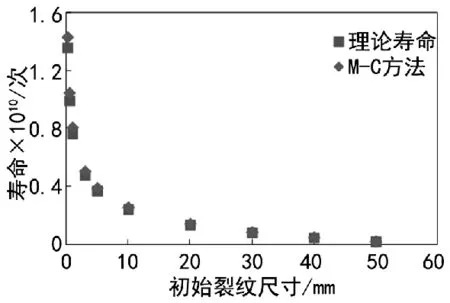
图4 确定性方法与M-C方法对比

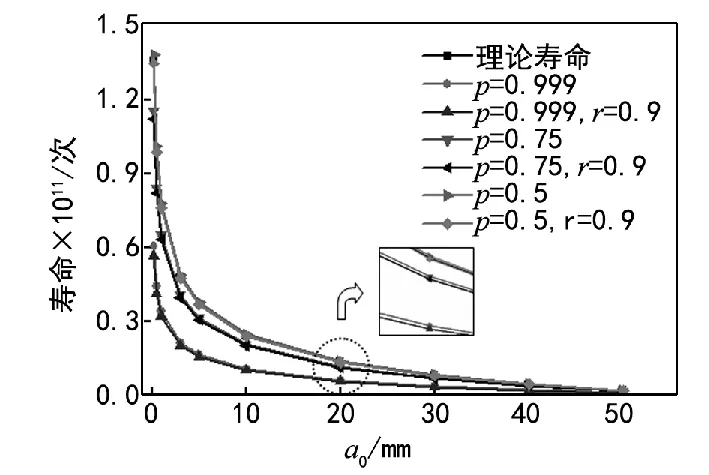
图5 不同初始裂纹尺寸下的疲劳寿命

从以上分析中可看出，用概率断裂力学方法依不同的可靠度给出不同的计算结果，由于它把各种参量均当作随机变量，用概率统计的方法处理，因此它得出的结果更可靠，更符合实际。

2.2 影响疲劳扩展寿命的因素

通过模拟发现，除了初始裂纹尺寸是重要的物理量之外，其他因素如扩展裂纹尺寸、断裂韧性、变异系数、气动载荷和转速等，对叶轮疲劳寿命均有影响，见图6～10。

图6为不同扩展裂纹尺寸下的疲劳寿命。由图6可知，当扩展裂纹尺寸接近零时，寿命趋于零，疲劳寿命随着扩展裂纹尺寸的增加而增加。在相同的扩展裂纹尺寸下，理论计算的疲劳寿命比考虑可靠度时的结果大，可靠度降低，疲劳寿命反而增加。

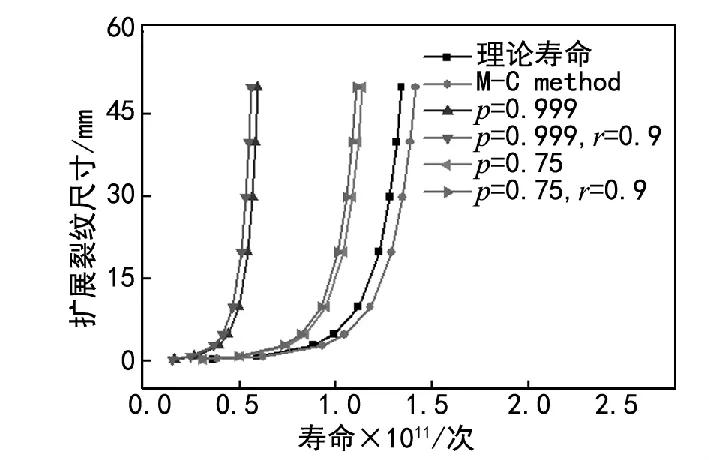
图6 不同扩展裂纹尺寸下的寿命

图7 为不同断裂韧性时的疲劳寿命。由图7可知，疲劳寿命随着材料断裂韧性的减小而降低;当KⅠc≈3 MPa·m1/2时，疲劳寿命趋于零。相同的断裂韧性下，当 p=0.999 时，寿命由 6.021×1010次下降到7.607×109次，r=0.9 时，寿命由 5.657×1010次下降到7.147×109次;当 p=0.75 时，寿命由 1.152×1011次下降到 1.455×1010次，r=0.9 时，寿命由 1.121×1011次下降到1.415×1010次。相同的断裂韧性时，可靠度越低，疲劳寿命越大;可靠度越高，疲劳寿命越小。考虑参数的不确定性和随机性时更加安全、可靠。

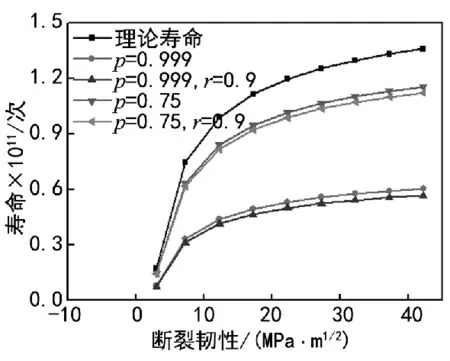
图7 不同断裂韧性下的疲劳寿命

图8 为不同变异系数时的疲劳寿命。相同的初始裂纹尺寸下，变异系数增大，疲劳寿命减小;变异系数减小，疲劳寿命增大，且寿命均随着初始裂纹尺寸的增大而减小。当a0=0.2 mm时，由图8(a)可知，变异系数为0.1时的寿命是0.3时的4.35倍;由图8(b)可知，变异系数为0.1时的寿命是0.3时的1.42倍。由此推断，应力变化范围Δσ的变异系数比材料常数C的变异系数对疲劳寿命的影响大。

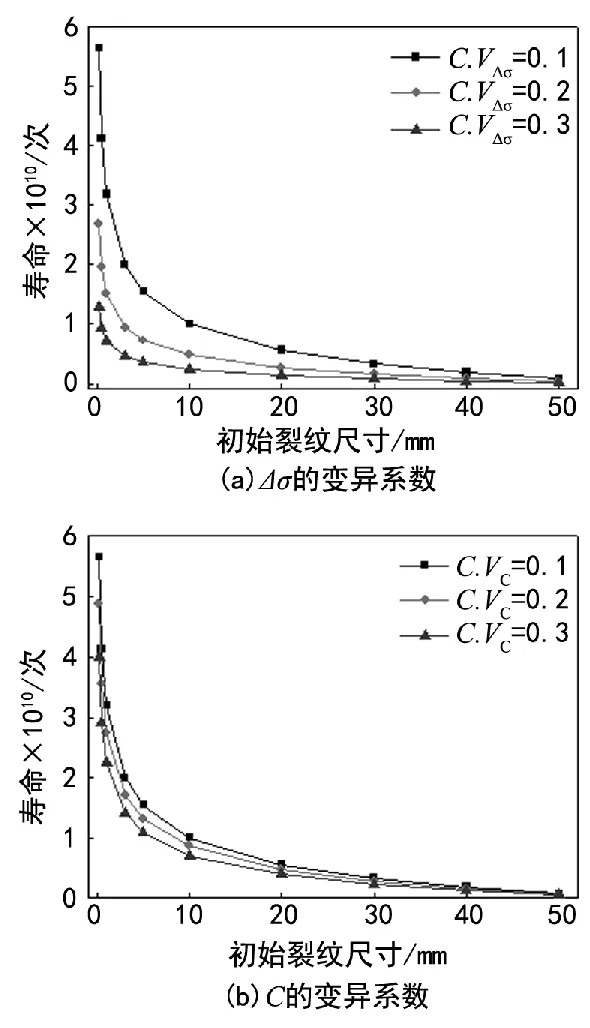
图8 不同变异系数系数下的疲劳寿命

图9 为不同气动载荷时的疲劳寿命。可看出，相同的初始裂纹尺寸下，疲劳寿命随着气动载荷的增加而降低;相同的气动载荷下，疲劳寿命随着初始裂纹尺寸的增加而减小。叶片表面在气动载荷作用下的应力低于材料的屈服强度，但是在这种较低能量的交变应力的长期作用下，叶片表面会形成高周疲劳，裂纹在高周疲劳的作用下逐渐扩展，最终叶片失效。图10为不同转速时的疲劳寿命。

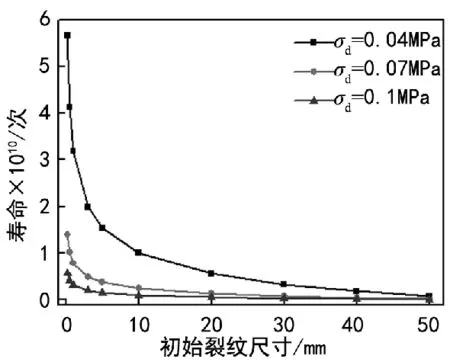
图9 不同气动载荷下的疲劳寿命

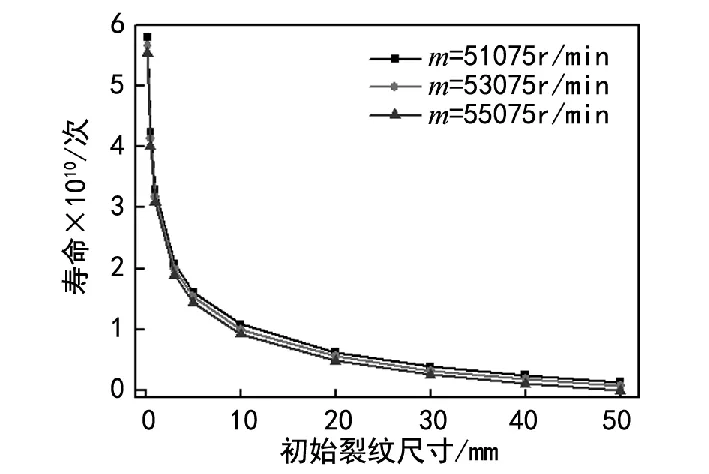
图10 不同转速下的疲劳寿命

由图10可看出，疲劳寿命随着初始裂纹尺寸的增加而减小，随着转速的增加而减小。转速和气动载荷的改变，均意味着应力幅值的改变:转速增大，应力幅值增大;气动载荷增大，应力幅值增大，且气动载荷的改变对应力幅值的影响较大。

3 结论

(1)Monte Carlo方法考虑了影响疲劳扩展寿命主要因素的不确定性和随机性，更接近于工程实际。理论求得的疲劳寿命曲线最陡，可靠度和置信度下求得的曲线坡度较小，结果更加安全、可靠。

(2)气动载荷是引起叶轮产生交变应力促使叶轮发生疲劳破坏的根本原因。叶片表面在较低能量的交变应力的长期作用下形成高周疲劳，裂纹在高周疲劳的作用下逐渐扩展，最终叶片失效。

(3)初始裂纹尺寸、断裂韧性、变异系数、气动载荷对疲劳寿命的影响较大。疲劳寿命随初始裂纹尺寸的增大而减小，随着断裂韧性的减小而减小，随着变异系数的增大而减小，随气动载荷的增大而减小。

(4)将PFM应用于叶轮的疲劳寿命预测中，克服了确定性评定方法的缺点，为相关叶轮的设计、检修提供了参考。

［1］ 舒林森，曹华军，许 磊，等.离心压缩机再制造叶轮结构特征三维建模方法及应用［J］.机械工程学报，2014，50(3):184-190.

［2］ 舒林森.离心压缩机再制造叶轮服役寿命预测模型及数值仿真研究［D］.重庆:重庆大学机械工程学院，2013.

［3］ Q.Li，J.Piechna，N.Müeller.Simulation of Fatigue Failure in Composite Axial Compressor Blades［J］.Materials and Design，2011，4(32):2058-2065.

［4］ M.M.Shokrieh，R.Rafiee.Simulation of Fatigue Failure in a Full Composite Wind Turbine Blade［J］.Composite Structures，2006，3(74):332-342.

［5］ Q.Chu，M.Zhang，J.Li.Failure Analysis of Impeller Made of FV520B Martensitic Precipitated Hardening Stainless Steel［J］.Engineering Failure Analysis，2013(34):501-510.

［6］ T.Kim，H.Lee.Failure analysis of MVR(machinery vapor recompressor)Impeller Blade［J］.Engineering Failure Analysis，2003，10(3):307-315.

［7］ 刘明霞，张海存，李德林，等.某离心压缩机叶轮断裂失效原因分析［J］.风机技术，2013(5):80-83.

［8］ J.C.Chávez，J.A.Valencia，G.A.Jaramillo，et al.Failure Analysis of a Pelton Impeller［J］.Engineering Failure Analysis，2015(48):297-307.

［9］ D.Nie，X.Chen，Z.Fan，et al.Failure Analysis of a Slot-welded Impeller of Recycle Hydrogen Centrifugal Compressor［J］.Engineering Failure Analysis，2014(42):1-9.

［10］ N.Ejaz，I.Salam，A.Tauqir.Fatigue Failure of a Centrifugal Compressor［J］.Engineering Failure Analysis，2007，7(14):1313-1321.

［11］ A.E.B.Abu-Elanien，M.M.A.Salama.A Monte Carlo Approach for Calculating the Thermal Lifetime of Transformer Insulation［J］.Electrical Power and Energy Systems，2012，1(43):481-487.

［12］ P.F.Liu，J.Y.Zheng.A Monte Carlo Finite Element Simulation of Damage and Failure in SiC/Ti-Al composites［J］.Materials Science and Engineering A，2006，1-2(425):260-267.

［13］ 赵少汴，王忠宝.抗疲劳设计-方法与数据［M］.北京:机械工业出版社，1997.

［14］ 吴家龙.弹性力学［M］.北京:高等教育出版社，2001.

［15］ 陈传尧.疲劳与断裂［M］.武汉:华中科技大学出版社，2001.

［16］ P.Paris，F.Erdogan.A Critical Analysis of Crack Propagation Laws［J］.Journal of Fluids Engineering，1963，85(4):528-533.

［17］ James W.Provan.Probabilistic Fracture Mechanics and Reliability［M］.Netherlands:Martinus Nijhoff Publishers，1987.

［18］ 麻栋兰.大型离心压缩机叶轮可靠性研究［D］.大连:大连理工大学，2009.

［19］ Y.L.Zhang，J.L.Wang，Q.C.Sun，et al.Fatigue Life Prediction of FV520B with Internal Inclusions［J］.Materials and Design，2015(69):241-246.

［20］ R.Zhang，S.Mahadevan.Fatigue Reliability Analysis Using Nondestructive Inspection［J］.Journal of Structural Engineering，2001，127(8):957-965.

Probability Failure Analysis of the Centrifugal Impeller

The fatigue life of the remanufacturing impeller can be predicted by using the Monte Carlo(M-C)method and the Probabilistic Fracture Mechanics(PFM)with consideration of the uncertainty and the randomness of the parameters.Results indicate that the M-C method with PFM method is more reliable and safer for the design of the impeller with comparison to the traditional fracture mechanics method.The initial crack length，the fracture toughness，the coefficient of variation and aerodynamic forces can significantly affect the remaining fatigue life of the impeller.PFM is applied to the fatigue life prediction of the impeller and provides reference for design and maintenance of the impeller.

PFM;impeller;M-C method;fatigue life?

TH452

A

1007-4414(2015)04-0001-05

2015-06-16

国家自然科学基金(编号:11172057);国家重点基础研究发展(973)计划(编号:2011CB013401);中央高校基本科研业务费专项资金和新世纪优秀人才支持计划。

张 昭(1979-)，男，河北衡水人，教授，博导，研究方向:工程力学。