考虑轴承影响的摆线针轮传动接触力分析*

姜 龙，许立新

(天津职业技术师范大学机械工程学院，天津)

0 引言

摆线传动中的轴承，作为构成机械系统转动运动副的核心部件，同时作为承载部件，其性能的优劣对系统的安全有效的运行起着决定性的作用［1］。由于轴承复杂的结构及接触特性，在进行刚体动力学仿真时，往往不考虑轴承之间的间隙、摩擦、阻尼及各种非线性因素，而把轴承视作一个理想的转动副，虽降低了仿真难度，却提高了仿真的误差。而随着现代机构如工业机器人、航空设备等向高速重载精密化方向发展，这种误差对于传动系统的影响已经不容忽视［2］。

近年来，国内外众多学者对摆线传动的受力特性进行了研究。国内谢明、汤修映、裘建新等在不考虑轴承的影响下利用仿真的方法分析了摆线传动中的接触力理论［3－5］。王文藻研究了现行摆线传动受力分析和计算方法存在的问题［6］。李充宁等对2K－V型行星传动中曲柄轴承上的载荷理论进行了分析［7］。而国外的M.BLAGOJEVIC等则研究了考虑摩擦力和离心力时传动中输入扭矩和负载扭矩间的关系［8］。同时轴承研究领域的刘玉兰也对轴承受单径向载荷时的载荷分布理论进行了细致的阐述［9］。

本研究以深沟球轴承6212为例，以轴承静力学和摆线传动模型为基础，基于UG和ADAMS建立了含深沟球轴承和不含深沟球轴承的摆线传动动力学虚拟样机对比模型，并在ADAMS中进行了仿真模拟分析，分析了有无转臂轴承对摆线传动模型的接触力响应带来的影响和当摆线轮施加一定外载荷，改变输入转速时转臂轴承的动载荷、受力变化规律分析及模型内部的接触特性分析。

1 摆线传动载荷理论分析

不考虑摩擦、间隙及轮齿的变形的影响，摆线轮在运动中主要承受三种载荷:

第一种载荷是针齿作用在摆线轮上的力P1，P2，P3……;力的作用线都沿啮合点的公法线方向，并相交于节点P。第二种载荷是柱销作用在摆线轮上的力Q，在此对比模型中直接施加一负载扭矩来代替其作用。第三种是转臂轴承作用在摆线轮上的合力RF'［10］。

1.1 针齿作用在摆线轮上的载荷

摆线轮的齿形是短幅外摆线的等距曲线，在任一时刻，总有一定数量的针齿与其啮合，产生啮合力，力的方向始终沿啮合线的公法线方向，且相交于节圆节点，而不存在啮合关系的针齿没有作用力，任一针齿与摆线轮间啮合力为:

其中:S=1+k21－ 2k1cos θbi

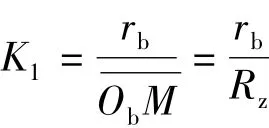
式中:θbi为节点、针轮分布中心针齿中心三者所组成的角度;Ma为摆线轮上的阻力矩;K1为短幅系数;Za为摆线轮齿数;Rz为针轮半径(针齿中心分布圆半径);rb为针轮节圆半径。

图1是摆线轮上作用力的分布图，Pi的方向都指向节点P。

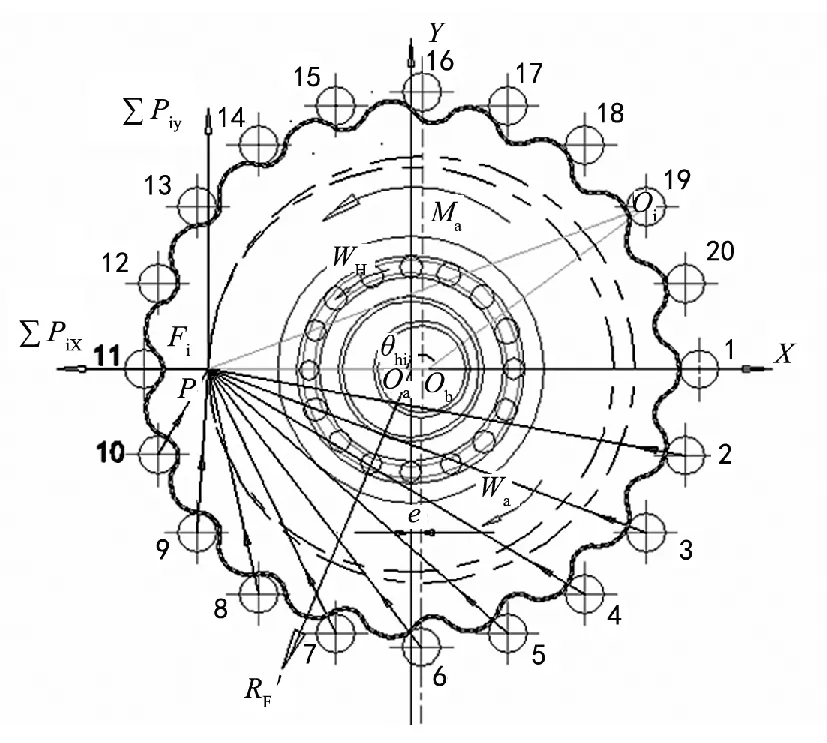
图1 摆线轮上作用力分布

1.2 转臂轴承作用在摆线轮上的合力

假设摆线轮静止不动，X轴上方的针轮有脱离摆线轮的趋势无接触力，而X轴下方的针轮与摆线轮逐渐啮合相接触，对摆线轮受力分析，如图1所示。

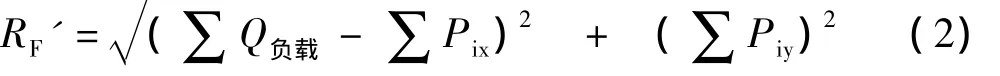
模型用等效扭矩代替柱销力对摆线轮的作用，根号项由一般取1.1近似计算。

对摆线轮节点P由力矩平衡:

RF'·rasin∂x=MaRF'力和X轴间的夹角，由图可得:

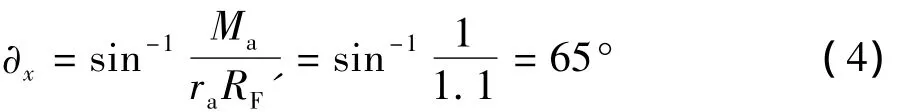
1.3 滚动轴承的载荷分布

由已有理论，当单个向心轴承受径向向下载荷RF时，内圈下沉δr，此时上半圈的滚动体不承受载荷，下半圈滚动体承受大小不同的载荷，最下面一个滚动体受力最大为F0，其中φ1是滚动体间夹角，Z是滚动体数目，如图2所示。

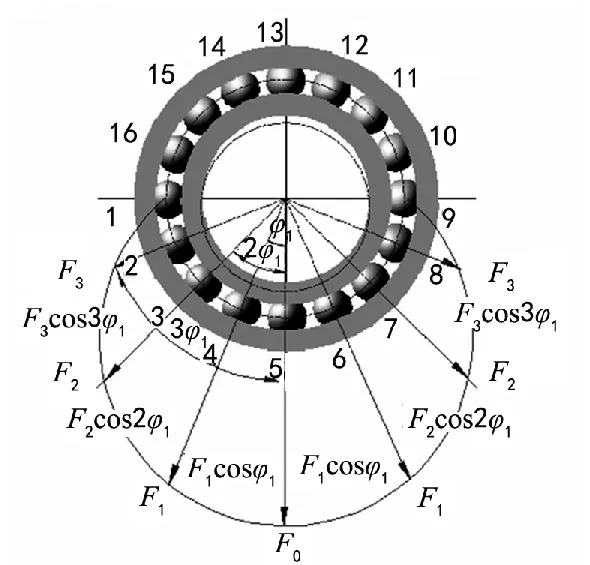
图2 轴承径向载荷分布

则Fo为:

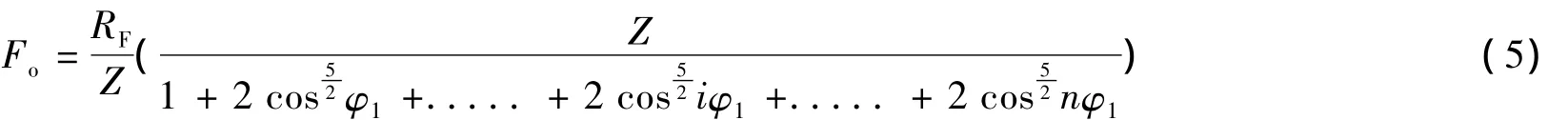
其中:

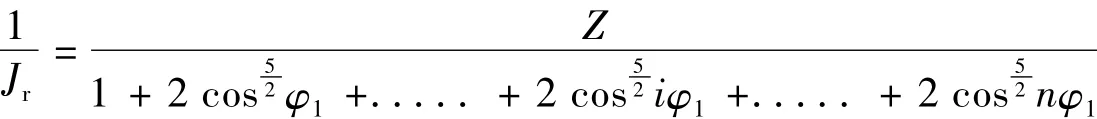
理论表明，当Z增加，1/Jr趋于一常数，球轴承取 4.37，滚子轴承取 4.08。

2 仿真模型的建立

含转臂轴承和不含转臂轴承的摆线针轮减速器虚拟样机采用UGII实现(见图3)。为了防止模型在导入ADAMS中时由于摆线轮上销孔的存在或输入轴上键槽的存在而使输入轴和摆线轮的质心在转动副转动平面内发生相对偏移，继而使摆线轮由于阻尼过大导致模型的仿真无法进行，图3中仅包含了仿真时涉及到的核心部件，同时去掉了轴上的键槽和摆线轮上的销孔及其之后不影响仿真分析的输出部件。

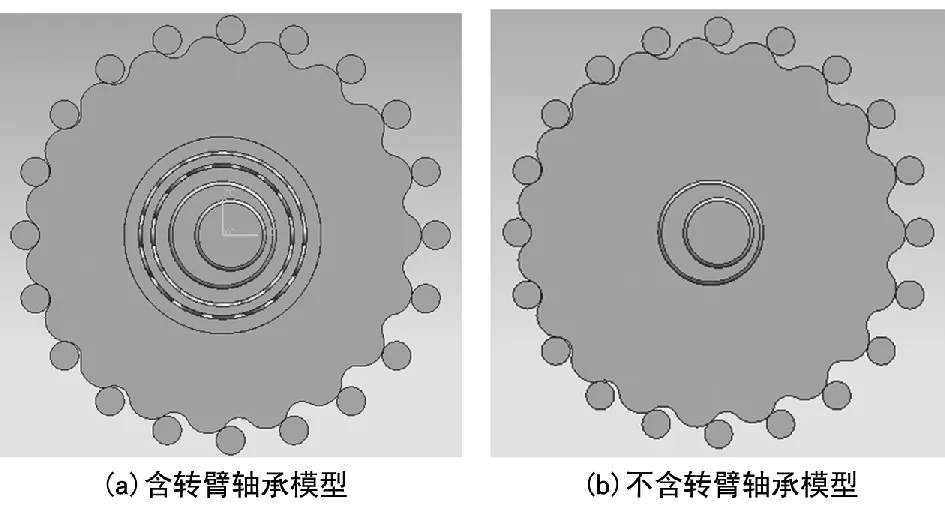
图3 含转臂轴承和不含转臂轴承的虚拟样机几何建模

由于针轮与摆线针轮的多齿啮合传动和转臂轴承结构的复杂性，在实际的运动中摆线轮、针轮及轴承内部之间的载荷分布受许多非线性因素影响。

2.1 虚拟样机中非线性因素的假设

用转臂轴承的力约束代替以往简化模型中的运动约束进行仿真本已十分复杂，若再考虑过多的非线性因素会使分析变得更加难以进行，为便于研究要精简非线性因素的种类，故此做出以下假设:①模型的制造误差忽略不计;②不考虑摆线轮、转臂轴承内外圈的弹性变形，假设滚动体与轴承内外圈滚道之间只存在局部弹性接触变形;③假设轴承的内圈与输入轴固连，而轴承的外圈与摆线轮的内孔相固连而无相对转动。

2.2 虚拟样机中约束的施加

(1)偏心轴的两轴段部分在ADAMS中要用固定副连接，而不可直接合并为成为一个部件，使偏心轴段的质心在转动平面内与摆线轮的质心不重合而难以仿真。

(2)轴承的内圈和偏心轴之间用固定副连接，轴承的外圈和摆线轮之间，针齿和大地间用固定副连接。

(3)轴承的滚动体和内外圈以及保持架之间，摆线轮和针齿间都施加接触。

(4)轴承的保持架和轴承的内圈之间，输入轴和大地间施加理想的转动副。

(5)模型的输入轴施加一恒定的输入转速。

3 虚拟样机动力学仿真结果分析

理论模型的动力学仿真是在工况摆线轮齿数Za=19传动比i=18输入转速分别为600 r/min，和60 r/min并分别在两种模型的摆线轮改变载荷TV=60 N·m施加条件下进行的。为了与理论分析进行对比，同时去掉仿真中惯性力对结果的影响，特加一组输入轴转速为0的静力仿真分析。

3.1 摆线轮与针齿之间的啮合力

图4表示连续5针齿在不同条件下同摆线轮的接触力作用情况。图5是输入轴转速为0时，含轴承模型加外载摆线轮与全部针齿之间的接触力图。图6是输入轴转速为60 r/min，含轴承模型加外载时摆线轮与另选连续5针齿间接触力图。

图4 连续5针齿转速600 r/min时接触力对比

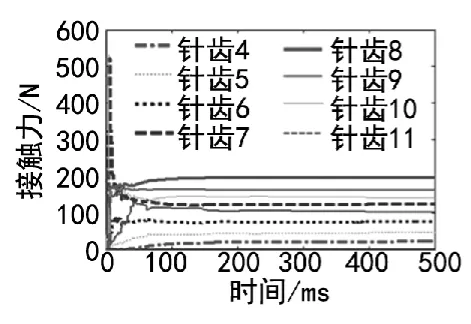
图5 全部针齿输入转速0时接触力

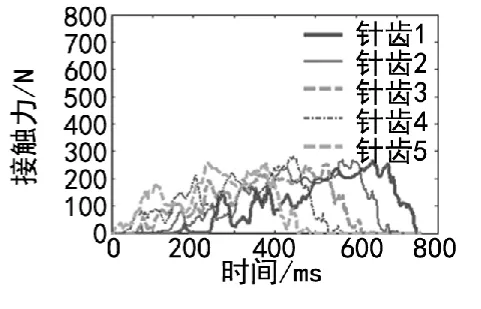
图6 连续5针齿转速60 r/min时接触力

对比分析:①在摆线轮与针轮的接触力幅值大小上，有轴承的一组比无轴承的一组在外载荷因素相同时要小一些，轴承的存在在一定程度上增加了系统的柔性，使得模型的刚度变小;②在摆线轮与针轮的接触力幅值波动范围上，在有无轴承因素相同时，加外载荷的一组明显比不加外载荷的一组幅值波动范围要平稳，外载荷的存在减小了轴与摆线轮之间的啮合间隙，从而削弱了摆线轮在运动过程中的振动，符合动力学特性;③摆线轮与针齿的接触力在某些位置发生跃变，是因为某一针齿与摆线轮脱离接触后，其它齿必然要承担全部载荷，从而引起齿对上的载荷突变;④从连续针齿受力情况来看，前一个针齿从进入啮合到退出都与其后的针齿受力情况大致相同，表明针齿与摆线轮间的接触力呈周期性变化;⑤不同转速下仿真结果对比，可知摆线轮与针齿之间的接触力大小与输入轴的转速在真实运动中也呈正相关，转速越大，同周期内接触时间也越短。

3.2 轴承滚动体的接触力分析

轴承受径向载荷时，内圈偏移下沉，最下面的滚动体受力最大。本模型中内圈所受到的径向合力与摆线轮对轴承外圈的合力成为一对平衡力，即单独分析轴承时轴承所受到的径向合力方向与轴承对摆线轮的合力方向一致。为了避免惯性力对接触力幅值带来的影响，把输入轴转速设置为0值。图7是含轴承模型加同上外载荷时滚动体与内齿圈的接触力图。

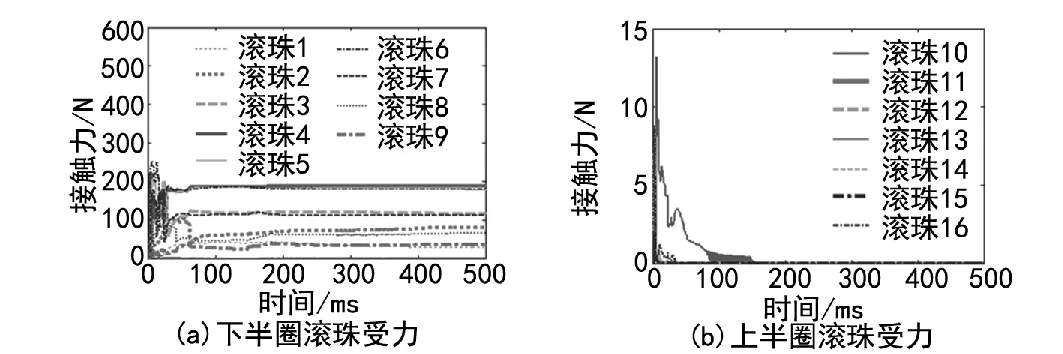
图7 全部滚珠输入转速为0时接触力

图1 状态时轴承只有下半圈滚珠1～9受力，上半圈滚珠10～16不受力且滚珠4在所有滚动体中所受接触力最大，表明轴承所受径向力的方向是由轴承中心指向滚珠4附近，其幅值最大为200 N左右。

3.3 理论计算与仿真结果对比

由于理论分析接触力时都是在不考虑模型内部摩擦力和离心力的作用下进行的，使得接触力理论值与真实值间总存在一定误差，为了更加直观准确的反映出模型中的接触力真实值变化情况，同时验证理论的正确性，故同时用仿真的方法进行了分析，并与理论分析进行对比。

短幅系数K1=rb/Rz=0.768 559，针轮节圆半径rb=K1Rz=AZb=88 mm，偏心距 A=4.4 mm，摆线轮节圆半径ra=rbZa/Zb=AZa=83.6 mm，摆线轮上的负载扭矩Tv=Ma=60 N·m，计算系数 Ky=0.379 769 542。由公式(3)，轴承所受到的摆线轮对其的径向作用力 RF=789.4N，方向由式(4)知与 X轴夹角65°，由式(5)，滚珠最大径向力 F0=215 N，同仿真图7反映基本相同。

实际中分析轴承受力时往往还要考虑轴承内部间隙的影响，模型中并没有考虑进去，故仿真分析实际上只是使分析值更加逼近了实际工况中的接触力幅值。两种分析方法显示结果基本一致，也验证了分析方法的正确性。

4 结论

(1)基于UG和ADAMS创建了含转臂轴承和不含转臂轴承的摆线针轮传动动力学虚拟样机仿真模型。模型中考虑了轴承的接触柔性、阻尼、摩擦等非线性因素，为工程上的摆线传动力分析提供了更为准确的依据。

(2)仿真分析表明，其他条件不变时，轴承的存在一定程度上减小了摆线轮和针齿之间的接触力大小，延长了单周期的接触时长。

(3)仿真研究表明，负载和输入转速同接触力的稳定性和幅值呈正相关性。

(4)理论分析结合仿真表明，任一时刻，轴承中总是只有一半滚动体受力，其幅值在同转速条件下与负载扭矩成正比，与摆线轮的节圆半径成反比。

［1］ Harris T A.Rolling Bearing Analysis［M］.New York:CNC Press，2001.

［2］ 许立新，李永刚，李充宁，等.轴承间隙及柔性特征对机构动态误差的影响分析［J］.机械工程学报，2012，48(7):30－36.

［3］ 汤修映，李 伟，王彩梅.行星摆线针轮减速机构的动力学虚拟仿真［J］.农业机械学报，2004，35(1):129－132.

［4］ 谢 明.摆线行星精密传动动力学理论研究及仿真［D］.重庆:重庆大学，2008.

［5］ 裘建新，叶 桦，姜少杰.ADAMS对长幅外摆线行星传动的动力学仿真［J］.机械设计，2004，21(12):48－50.

［6］ 王文藻.摆线行星齿轮传动的受力分析［J］.研究·开发，2001，39(444):29－30.

［7］ 李冲宁，孙 涛，刘继岩.2K－V型行星传动的结构和力的分析［J］.机械传动，2000，24(2):7－9.

［8］ M.Blagojevic，M.Kocic，N.Marjanovic，B.et al.Influence of the Friction on the Cycloidal［J］.Journal of the Balkan Tribological Association，2012，18(2):217－227.

［9］ 刘玉兰，孙澜涛.滚动轴承载荷分析［J］.山东建材学院学报，1999，13(2):163－165.

［10］ 郑州工学院机械原理及机械零件教研室.摆线针轮行星传动［M］.郑州:科学出版社，1978.