基于区间FTA树的液压柱塞泵可靠度分析*
2015-06-11邓耀初邓季贤刘相新王艳荣
邓耀初,邓季贤,刘相新,王艳荣
(1.北京航天发射技术研究所,北京 100076;2.西安电子科技大学,陕西 西安 710071)
0 引言
液压柱塞泵是液压系统的关键元件,是整个液压系统的“心脏”,它向液压系统的执行元件(液压马达、液压缸等)提供一定压力、流量的液体,从而保证执行机构的正常工作。柱塞泵性能的优劣对液压系统的工作可靠性影响重大[1]。
随着现代工业的发展,柱塞泵在各个领域得到了相当广泛的应用,它的功能越来越多,自身的结构也越来越复杂,从而导致了它的失效率也随之增多。喻国哲[2]分析了柱塞泵的泄露机理,利用故障树对泵的可靠性进行了研究,得到泵的可靠度。马纪明、詹晓燕[3]对影响柱塞泵流量的参数及退化路径进行分析,根据柱塞泵的可靠性判据,给出了柱塞泵的可靠性分析方法。
传统的故障树分析故障发生的概率处理成精确值,但是在实际中我们无法获取关于柱塞泵比较充分的数据,传统的FTA树分析受到限制,因此提出了基于证据理论的区间FTA分析法。
1 区间FTA分析法的基本思想
在实际工程中,尤其是像液压柱塞泵这种大型产品,无法拿出较多的产品来进行试验从而获得更多的试验数据,因此传统故障树中有些底事件的故障概率很难精确地估计出来。
证据理论(D-S理论)[4]是一种研究不确定性、不知性的数学理论,更适合应用于数据较少的产品可靠性计算。D-S理论不仅能获取故障树每个底事件的故障区间,而且结合了专家们的不同观点,避免出现偏见。
故障树区间分析法引入了D-S理论和区间分析,D-S理论的似然函数和信任函数分别作为实际概率的上下界,作为底事件的故障概率区间,根据区间分析理论可以确定出顶事件的失效概率区间。
1.1 D -S理论
证据理论是将证据集合划分为几个不相关的部分,并利用它们对辨识框架进行独立判断,然后用Dempster组合规则将其组合起来,合成多个证据源提供的证据,经组合之后所得到的组合证据的可信度提高,证据合成公式[5]如下:
对于∀A⊆Θ,识别框架Θ上的有限个mass函数m1,m2,…,mn的 Dempster组合规则为:

式中:K为归一化因子:

1.2 区间FTA分析法的区间算子[5]
区间FTA分析法与传统的FTA树相比,最大的特点是区间FTA树应用的是区间算子,包括与门区间算子、或门区间算子及表决们区间算子,公式如下:

求得FTA树区间算子,对故障树进行区间分析,得到顶事件的失效概率也为一区间数。
2 液压柱塞泵的故障树建立
在建立故障树之前,应该对液压柱塞泵系统及其组成部分有充分的了解,将最不想看见的故障作为顶事件,从顶事件开始,由上往下逐级分析,直到不能再往下分解为止,这样可以防止在建树遗漏某些故障原因,液压柱塞泵的原理见图1。

图1 液压柱塞泵主体部分的工作原理
在对液压柱塞泵故障树分析中,将“柱塞泵不正常工作”作为故障树的顶事件,然后开始进行故障分析,在分析中假设:
(1)所分析的液压柱塞泵系统及其组成部件只有两种状态-故障或正常。
(2)各个底事件之间相互独立。
(3)不存在外界干扰因素。
通过对液压柱塞泵不正常工作进行分析,对其故障原因建立故障树如图2所示。其中,故障树中事件的含义[6]分别为:
T:柱塞泵不能正常工作;A1:柱塞泵咬死;A2:柱塞泵轴向失衡;A3:系统外泄严重;A4:系统输出量不足;A5:系统超压;A6:系统压力不足;B1:系统介质精度太差;B2:柱塞泵发生气蚀;X1:系统发热严重;X2:系统过滤精度较差;X3:摩擦副严重磨损;X4:柱塞泵吸入口进气;X5:系统密封条件变差;X6:柱塞泵装配不当;X7:柱塞泵元件磨损严重;X8:柱塞泵平衡油路不通;X9:柱塞泵平衡块破坏;X10:柱塞泵机械密封失效;X11:柱塞泵计入阻力过大;X12:真空表显示故障;X13:流量计显示故障;X14:其他原因;X15:电接点压力级显示故障;X16:柱塞泵旁路阀泄漏严重;X17:电接点压力表低压力级显示故障。
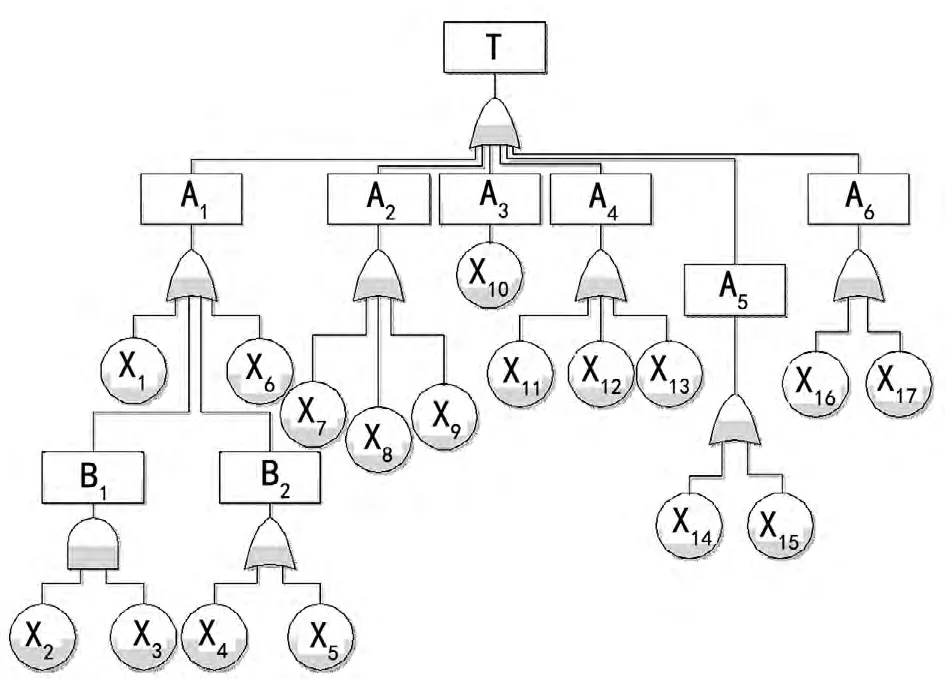
图2 液压柱塞泵的故障树
根据上行法可以得出故障树的最小割集为:{X1、X2}、{X3}、{X4}、{X5}、{X6}、{X7}、{X8}、{X9}、{X10}、{X11}、{X12}、{X13}、{X14}、{X15}、{X16}、{X17}。
3 液压柱塞泵系统的故障分析
对上述故障树进行分析,得到顶事件顶事件与中间事件以及底事件的关系为:
T=A1∪A2∪A3∪A4∪A5∪A6
其中:A1=B1∪B2∪X1∪X6,A2=X7∪X8∪X9,A3=X10,A4=X11∪X12∪X13,A5=X14∪X15,A6=X16∪X17,B1=X2∩X3,B2=X4∪X5。
在求得顶事件的故障概率之前,首先必须确定各个底事件发生故障的概率区间,通过搜集相关资料,以及结合不同专家的经验,根据D-S理论通过Dempster组合规则确定出底事件失效概率如表1。
已知了底事件的失效概率区间之后,就可以根据上述故障树区间算子求解方法求得故障树中的或门区间算子为:
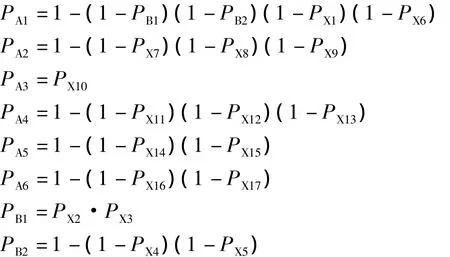
则顶事件的故障概率区间为:

将表1中的底事件失效概率区间带入公式中,可以得到顶事件的故障概率区间为:
PT=[0.0969 ×10-4,0.4050 ×10-4]
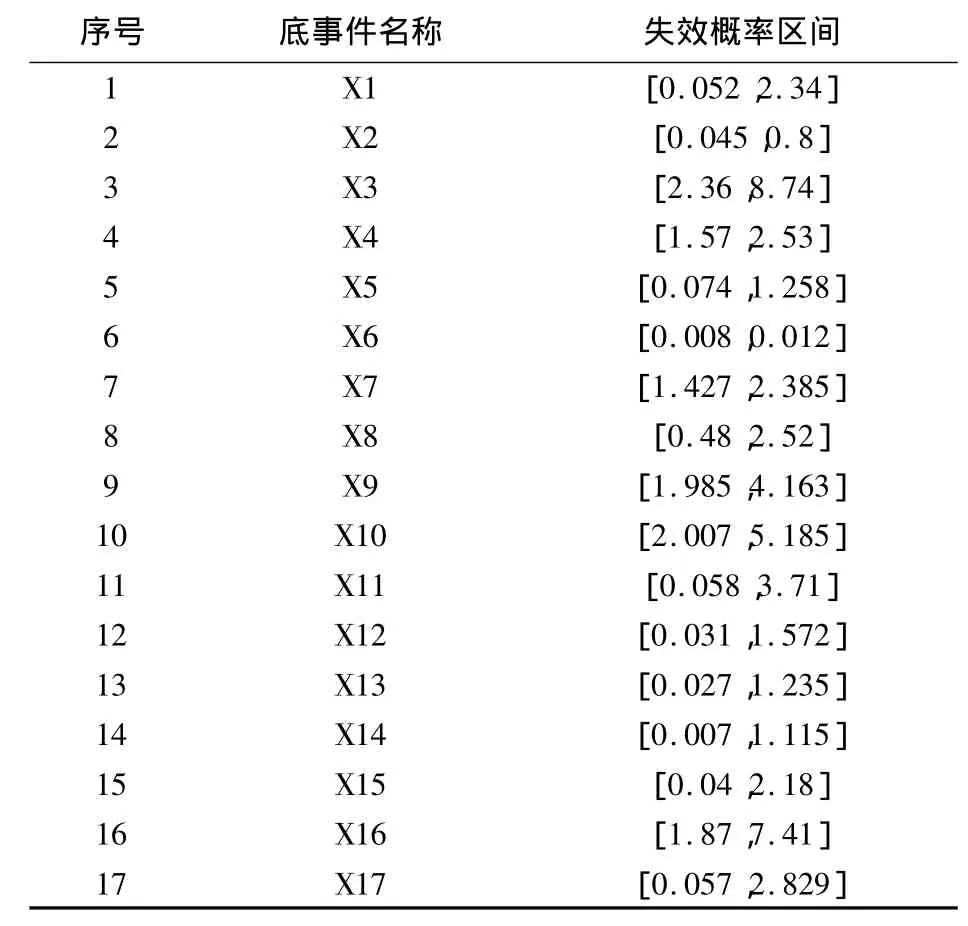
表1 故障树底事件失效概率区间 (×10-6/h)
液压柱塞泵中的摩擦副不可修复,因而摩擦副决定了泵的使用寿命,因此我们着重对液压柱塞泵摩擦副的失效进行分析,摩擦副的失效主要是磨损导致的,也就是上述故障树中的底事件X3。对摩擦副在标准试验工况下进行实验室模拟研究,结合工程实际,规定当摩擦副磨损掉的间隙量达到50 μm的时候认为摩擦副失效,即柱塞泵失效,选择外形为φ50×φ 34×10 mm的钢材作为试样,选择初始试验时摩擦副的磨损间隙为75 μm,取试验时间间隔为30 min,则对试验数据进行最小平方逼近可得到初始磨损间隙为75 μm时的磨损方程[7]为:
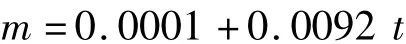
假设t0=0时摩擦副的失效概率区间为p0=[2.36 ×10-6,8.74 ×10-6],由上述顶事件概率可知此时液压柱塞泵的失效概率区间为:T0=[0.0969×10-4,0.4050 ×10-4],此时摩擦副的磨损量为 m0=0.0001 g。
当液压柱塞泵工作到400 h时,即t1=400 h,根据磨损方程我们得出此时摩擦副的磨损量为m1=3.6801 g,对磨损量进行归一化处理,则归一化常数为:
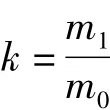
则此时摩擦副的失效概率区间为:p1=kp0=[0.0869,0.3216],根据顶事件计算公式可得到液压柱塞泵在t1=400 h时的失效概率区间为:T1=[0.970×10-4,0.4076 ×10-4]。
依照上述方法,取时间t2=800 h,t3=1 200 h,t4=1 600 h,根据磨损方程得出在各时间时的磨损量为 m2,m3,m4,同样地对磨损量进行归一化,最后得出液压柱塞泵在各个时间时的失效率及可靠度。所得结果如表2所列。

表2 柱塞泵的可靠度随时间的变化
由表2可知,随着时间的延长,摩擦副的磨损量随之增多,失效概率区间变大,从而柱塞泵的失效概率区间也在变大,也就是说,液压柱塞泵的可靠性随时间的增长而降低。
4 结语
通过对液压柱塞泵的故障进行分析,建立了区间FTA树,通过D-S证据理论对各个证据的来源进行组合,最终得出底事件的失效概率区间,进而得到柱塞泵的失效概率区间;在影响柱塞泵的底事件中,属摩擦副磨损对液压齿轮泵的影响最大,因而研究了随着时间增长,摩擦副磨损对柱塞泵寿命的影响,可知随着磨损量的增加,柱塞泵的失效概率变大,可靠度变低。
[1] 赵丙文,李 锐.基于规则的轴向柱塞泵故障诊断专家系统设计与应用[J].机械工程师,2010(10):66-68.
[2] 喻国哲.全水润滑斜轴式海水柱塞泵改进及其可靠性分析[D].北京:北京工业大学,2013.
[3] 马纪明,詹晓燕.具有随机退化特性的柱塞泵性能可靠性分析[J].机械工程学报,2010,46(14):189 -193.
[4] 张新峰,赵 彦,施浒立.基于D-S理论的故障树区间分析方法[J].机械科学与技术,2010,26(5):659 -661,667.
[5] 林立广,陈建军,马 娟.大型星载天线展开系统故障树的区间分析方法[J].机械强度,2010,32(1):68 -73.
[6] 董浩然,林少芬.液压柱塞泵故障树分析[C].2007年全国机械可靠性学术交流会论文集[A].2007.
[7] 贾瑞清,夏志新.液压元件污染磨损寿命的实验室模拟研究[J].液压与气动,1994(3):4 -8.
