矩阵方程Xα+A*X-βA=I的Hermite正定解

2015-06-10伍国兴商绍强

陕西师范大学学报（自然科学版） 2015年3期

关键词：理学院林业大学不动点

梁丽，伍国兴＊，陈飞, 商绍强

(1 东北林业大学理学院，黑龙江哈尔滨 150040;2 北京信息科技大学理学院，北京 100192)

矩阵方程Xα+A*X-βA=I的Hermite正定解

梁丽1，伍国兴1＊，陈飞2, 商绍强1

(1 东北林业大学理学院，黑龙江哈尔滨 150040;2 北京信息科技大学理学院，北京 100192)

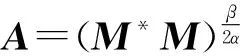
矩阵方程；正定解； CS分解; Brouwer不动点定理

考虑矩阵方程

Xα+A*X-βA=I,

(1)

其中A∈Cn×n，I是n×n阶单位矩阵，A*表示矩阵A的共轭转置矩阵，α、β均为正整数且β<α。近来，已经有许多学者对形如(1)式形式的矩阵方程进行了研究[1-7]。当α=1，β=1或β=2时的方程是从控制理论[1-3]、动态规划[8]、随机过滤[2]、统计学中推导出来的。本文将研究矩阵方程(1)正定解存在的充要条件，并利用Brouwer不动点定理[5]求解。

1 引理

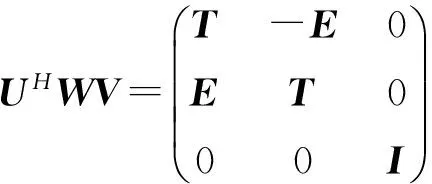
其中T=diag(γ1,γ2,…,γl)≥0,E=diag(σ1,σ2,…,σl)≥0,I为n-2l阶单位阵。

引理2如果A≥B>0(或者A>B>0)，则当δ∈(0,1]时，有Aδ≥Bδ>0(或者Aδ>Bδ>0)；当δ∈[-1,0)时，有Bδ≥Aδ>0(或者Bδ>Aδ>0)。

2 矩阵方程Xα+A*X-βA=I正定解存在的充要条件

(2)

将(2)式变形得

M*M+(M*)-β/αA(M*)-β/αA=I。

(3)

即

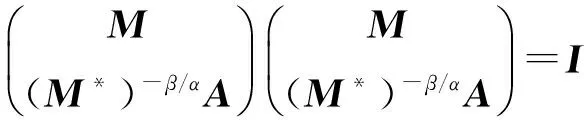
(4)

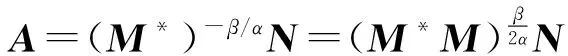
M*M+N*N=I。

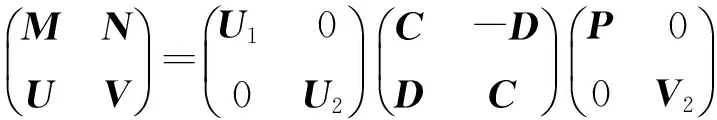
(5)

根据分块矩阵的乘法法则,将(5)式变形得

(6)

则M=U1CP，N=U2DP。由于M是Hermite正定阵，故C>0。令Q=PU2可知，Q为酉矩阵，C2+D2=I。

充分性。若存在酉矩阵P、Q和对角矩阵C>0,D>0，且C2+D2=I,CP=PC，使得

P-1=P*，(P-1)*=P。

P*C2P+P*D2P=I

3 利用Brouwer不动点定理求解

证明令

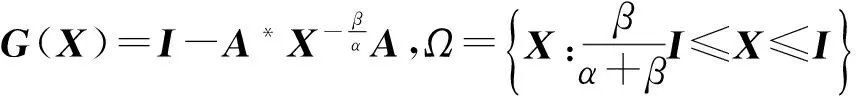
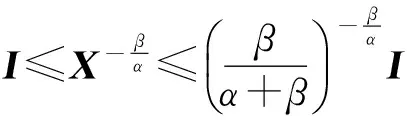
(7)

故

(8)

即

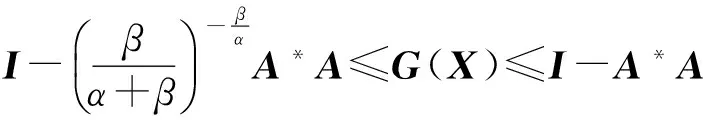
(9)

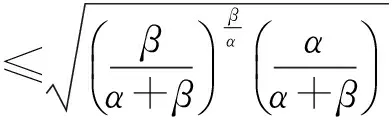
(10)

即

(11)

将(11)式代入(9)式，可得

I-A*A≤I。

(12)

即

(13)

4 结语

本文应用Hermite正定矩阵和酉矩阵，得到了矩阵方程Xα+A*X-βA=I存在正定解的两个充分必要条件，然后利用Brouwer不动点定理给出了该矩阵方程在一定条件下，在特定矩阵区间上有解的结论。但本文是基于α、β均为正整数且β<α时进行的研究，故存在一定的局限性。今后，可对当α、β为实数时进行更为广泛的研究。

[1] Cai J,Chen G L.Some investigation on Hermitian positive definite solutions of the matrix equationX+A*X-1A=Q[J].Linear Algebra and its Applications, 2009, 430: 2448-2456.

[2] Li Zhaoyan，Zhou Bin, Lam James.Towards positive definite solutions of a class of nonlinear matrix equations[J].Applied Mathematics and Computation, 2014, 237: 546-559.

[3] 尹小艳.几类非线性矩阵方程的Hermite正定解及其扰动分析[D].西安：西安电子科技大学理学院，2009.

[4] Liu X G, Gao H.On the positive definite solution of the equationXS±ATX-tA=I[J].Linear Algebra and its Applications, 2003, 368: 83-97.

[5] Yang Yueting.The iterative method for solving nonlinear matrix equationXS+A*X-1A=Q[J].Applied Mathematics and Computation, 2007, 188: 46-53.

[6] Salah M,Ei-sayed. An algorithm for computing positive definite solutions of the nonlinear matrix equationX-A*X-1A=I[J].International Journal of Computer Mathematics, 2003, 80: 1527-1534.

[7] Zhang Yuhai. On Hermitian positive definite solutions of matrix equationX+A*X-2A=I[J].Linear Algebra and its Applications, 2003, 372: 295-304.

[8] Duan Xuefeng, Wang Qingwen,Li Chunmei.Positive definite solutions of a class of nonlinear matrix equation[J].Linear & Multilinear Algebra, 2014, 62(6): 839-852.

〔责任编辑宋轶文〕

The Hermitian positive definite solution of the matrix equationXα+A*X-βA=I

LIANG Li1,WU Guoxing1*,CHEN Fei2, SHANG Shaoqiang1

(1 College of Science, Northeast Forestry University, Harbin 150040, Heilongjiang, China;2 College of Science, Beijing Information Science & Technology University, Beijing 100192, China)