关于k次补数的一个恒等式

李 扬

(西北大学 数学学院，陕西 西安 710127)



关于k次补数的一个恒等式

李 扬

(西北大学 数学学院，陕西 西安 710127)

初等方法； 解析方法；k次补数； 恒等式

对于任意正整数n，定义ak(n)为n的k次补数，使得nak(n)成为完全k次幂数的最小正整数。例如a2(n)=2,a3(n)=4,a4(n)=8,ak(n)=2k-1,文献[1]建议研究k次补数的性质。许多学者进行了研究[1-10]，得到了如下几个恒等式：

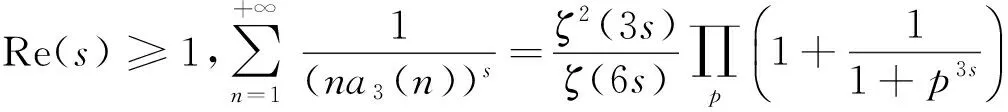
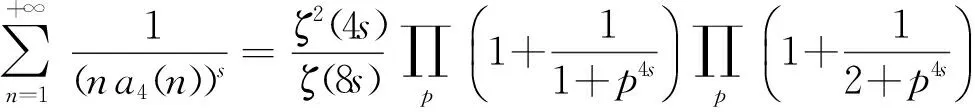
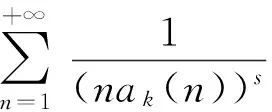
定理1对于任意的复数s且满足Re(s)≥1，当正整数k>1时，有

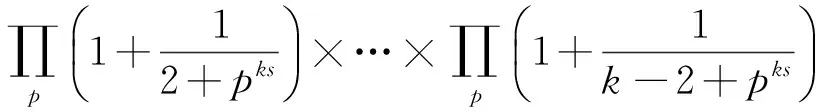
1 引理及其证明

本节利用初等及解析方法给出定理的证明，为方便后续的证明，首先给出下面几个引理。

引理1首先定义函数F(t)如下:

这里t、k均为正整数且k>1,1≤t≤k-1。而b2、b3、…、bk-t为两两互素的正整数，即

(b2,b3)=1, (b2b3,b4)=1,…,

(b2b3…bk-1,bk)=1,且b2、b3、…、bk-t均为无平方因子数，即p|bi且p2⫮bi(2≤i≤k-t,i∈N)。其中s为实部大于1的任意复数,p为任意素数。μ(n)为Möbius函数，这里有

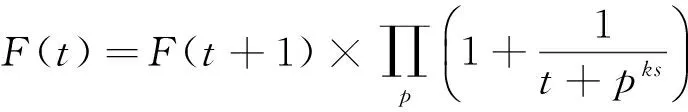
证明

实际上就是F(t+1),因此，得到如下结论：

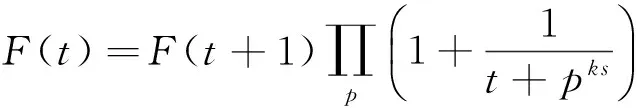
引理2对于任意的复数s且满足Re(s)≥1，其中k为正整数且k>1,则有恒等式：

证明在引理1中分别令t=1,t=2,t=3,…,t=k-3就可以得到以下等式：

⋮

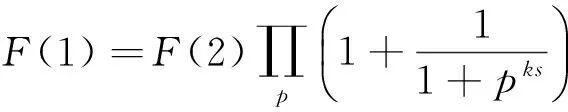
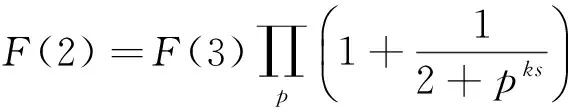
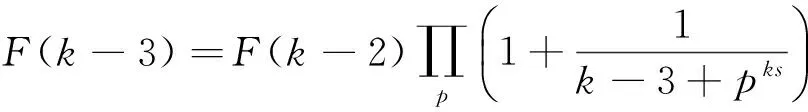
将上述k-3个等式左右两端相乘可得：

(1)

其中，F(k-2)还需要进行计算。

将上面的级数变成级数的Euler乘积形式，可得

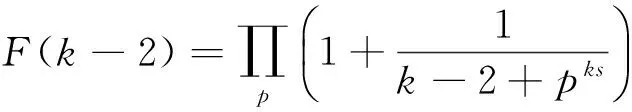
(2)

将(2)式代入(1)式可得

这样,引理2得证。

2 定理的证明

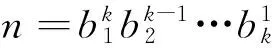
应用引理2，就可以得到

这样，定理1得证。

[1]SmarandacheF.Onlyproblems,notsolutions[M].Chicago:XiquanPublishingHouse,1993.

[2]TomMApostol.Introductiontoanalyticnumbertheory[M].NewYork:Springer-Verlag,1976.

[3]SergioFalcon.Onk-Fibonacci sequences and polynomials and their derivatives[J].Chaos,Solitons and Fractals,2009,30:1005-1019.

[4] Zhang Wenpeng.Some identities involving the Fibonacci numbers and Lucas numbers[J].The Fibonacci Quarterly,2004,42:149-154.

[5] Ma Rong,Zhang Wenpeng.Several identities involving the Fibonacci numbers and Lucas numbers[J].The Fibonacci Quarterly,2007,5:164-171.

[6] 张文鹏，李海龙.初等数论[M].西安：陕西师范大学出版社，2008.

[7] 潘承洞，潘承彪.解析数论基础[M].北京：科学出版社，1991.

[8] Ohtsuka H,Nakamura S.On the sum of the reciprocal of Fibonacci numbers[J].The Fibonacci Quarterly,2009,46:153-159.

[9] Zhang W,Wang T.The infinite sum of the reciprocal of Pell numbers[J].Applied Mathematics and Computation,2012,218:6164-6167.

[10] Zhang G.The infinite sum of the reciprocal of Pell nubmers[J].Journal of Mathematical Research and Exposition,2011,31:1030-1034.

〔责任编辑 宋轶文〕

An identity aboutk-th power complement

LI Yang

(School of Mathematics, Northwest University, Xi′an 710127, Shaanxi, China)

elementarymethod;analyticmethod; k-thpowercomplement;identity

11M06

1672-4291(2015)03-0010-03

10.15983/j.cnki.jsnu.2015.03.133

2014-09-22

国家自然科学基金资助项目(11371291)

李扬，男，博士研究生，研究方向为解析数论。E-mail:ly13119143216@126.com

O177.1

A