内河电力推进游轮振动数值仿真及试验研究
2015-06-10杨敬东王智祥孙勇敢王红梅
杨敬东,王智祥,孙勇敢,王红梅
(重庆交通大学 航运与船舶工程学院,重庆 400074)
内河电力推进游轮振动数值仿真及试验研究
杨敬东,王智祥,孙勇敢,王红梅
(重庆交通大学 航运与船舶工程学院,重庆 400074)
针对首艘内河电力推进豪华游轮中、艉部区域出现的有害振动问题,采用MSC-PATRAN软件等对游轮整体及局部结构进行仿真计算;对结构总体及局部的激励源、振动形式及固有频率进行了研究,并与实船试验数据对比分析,验证了理论分析及数值仿真计算的可靠性;进一步总结探讨引起该船在振动方面出现问题的原因,并提出了相应船舶减振的建议措施。
船舶工程;船舶有害振动;仿真分析计算;船舶减振
为了解内河豪华游轮船体结构、上层建筑、机舱及局部结构的振动性能,预防过大振动的产生,因此需对本船进行船体振动计算分析,实船振动试验,并使振动水平能满足相关标准的要求。
船为钢质船舶,首柱前倾。各主要甲板首尾贯穿,机舱在尾部。总长为141.8 m,垂线间长132.0 m,型宽19.0 m,设计吃水2.9 m,设计航速24.0 km/h,主推进电机型号及台数为4台,额定功率为680 kW, 舵桨减速比为2.769:1,螺旋桨型式为全回转舵浆, 舵桨叶片数为4叶。中纵剖面见图1。
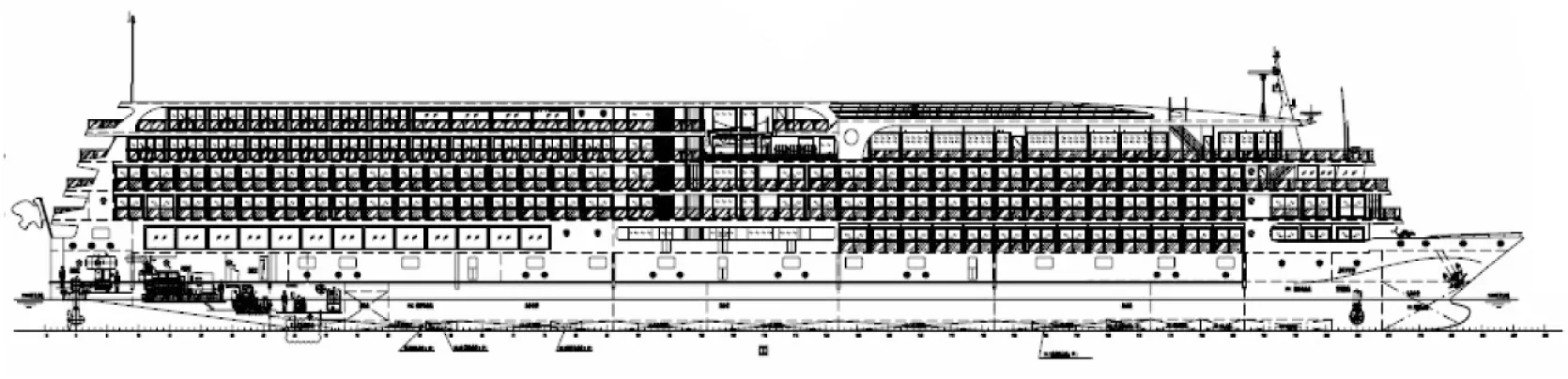
图1 内河电力推进豪华游轮总布置Fig.1 General arrangement plan of inland electric propulsion luxury cruise ship
笔者通过概述船舶振动的振源、振动形式及减振方法,对内河电力推进豪华游轮采用迁移矩阵法进行了整体结构固有频率和固有振型的计算,同时利用MSC PANTRAN/NASTRAN软件对该船做了有限元建模和分析,计算了船舶固有频率、固有振型,特别对船艉部餐厅处出现的局部有害振动进行了分析,给出了减振措施,有效地减少了有害振动,为同类型船舶的减振措施及解决船舶振动的方法提供了有益的借鉴。
1 总体振动计算方法
1.1 总体自由振动计算
当弹性结构置于流体介质中时,流体与结构之间通过它们的交界面存在着相互作用。当用有限元方法计算结构振动与声耦合问题时,需要对结构和流体都进行有限元网格离散,建立有限元方程进行分析。
1.2 总体动力响应计算
对弹性结构与声介质耦合振动的矩阵方程方程两边进行拉氏变换并利用模态转换[1],可得:
(-ω2Mτ+jωCτ+Kτ)Q(ω)=Fτ(ω)
(1)式中:Mτ为模态质量矩阵,Mτ=ΦTMΦ;Cτ为模态阻尼矩阵,Cτ=ΦTCΦ;Kτ为模态刚度矩阵,Kτ=ΦTKΦ;F(ω)τ为模态力向量,F(ω)τ=ΦTF(ω);Q(ω)为模态列阵。
由系统微分方程解耦, 变换为n个独立的在模态坐标中的微分方程,由这些解耦的微分方程,可以解得系统各点在频域中的振动响应。
1.3 激振力计算
一般而言,引起船体结构振动的主要激振源有主机和螺旋桨。对于本船来说,根据柴发电机组资料,设备基座采用双层隔振装置[2],理论计算及实船测试,均显示激振力很小。因此,在确定激振力频率时不考虑主机激振力频率而仅考虑螺旋桨激振力频率。
由于本轮没有脉动压力桨模试验数据,螺旋桨激振力采用霍尔顿法公式估算,其叶频力计算公式如式(2)~式(5)[3]:
空泡分量
(2)
非空泡分量
(3)
脉动压力
(4)
激振力
Fp=ΔPZ·ka·T0·10-5
(5)
主要的螺旋桨激振力频率为螺旋桨叶频、倍叶频激振力频率。其中:螺旋桨最高转速时的频率值为:螺旋桨转速为361.2 r/min;叶频激振力频率为24.08 Hz;倍叶频激振力频率为48.16 Hz。
按照式(2)~式(5)可计算得到螺旋桨叶频脉动压力在满载时为2.15 kPa,压载时为2.27 kPa。根据经验,螺旋桨倍叶频脉动压力值一般可取为叶频脉动压力值的0.4~0.5倍。
上层建筑板和板格局部结构固有频率必须满足高于26.48 Hz,上层建筑板架的固有频率必须高于26.48 Hz或低于21.67 Hz[4]。
2 游轮结构振动特性计算
针对内河电力推进游轮大跨度甲板板架、贯通式上层建筑等船体结构特点,对其船体结构振动的计算研究分为三个部分:①利用一维梁模型方法对船体梁总振动进行研究分析,包括研究计算船体梁的总振动,确定船体梁总振动的固有频率和固有振型;②局部结构振动研究分析,主要是对船体上层建筑内板、板格等局部结构进行振动计算校核,使结构频率储备达到一定要求;③整船有限元振动计算分析,主要是通过建立整船三维有限元模型,进行船体总振动和船体各部位板架局部结构的振动计算,确定船体总振动和板架结构的固有频率,以及螺旋桨激振力作用下的船体振动响应,全面掌握整个船体结构的振动特性[5]。
2.1 一维梁模型方法振动计算
一维梁模型总振动分析采用迁移矩阵法进行计算,将变剖面的船体梁近似地看作由许多等剖面的船体梁组成,且假定在每一船梁段的质量和刚度是均布的。计算中,船梁长度用两柱间长L=132.0 m,船梁的分段用站号将船长划分为20段,即21站,在各段内的梁段看作为均匀等值梁,各段有相应的梁段长度l=L/20 = 6.6 m,其计算值如表1。

表1 船体总振动固有频率计算结果
一般而言,引起船体总振动的激振力主要有螺旋桨工作时产生的轴频、叶频激振力和主机1阶、2阶不平衡力和力矩。本船的主机是MAN 6L21/31,该机性能良好,不存在1阶、2阶不平衡力和力矩。
在主机额定工况下,桨轴转速为361.2 r/min,螺旋桨叶频为24.08 Hz。从计算结果看,叶频已超过船体垂向总振动前5阶固有频率;因此,螺旋桨叶频能避开共振,不会引起明显船体垂向总振动。
2.2 整船三维有限元振动计算
2.2.1 计算模型
在进行有限元分析时,关键是要建立正确的模型与选择适当的单元,以求得精确的结果。本船船体实际结构非常复杂,必须对模型做适当的简化,合理的分配到船体强构件上,以避免不必要的局部振动影响到总振动的结果,计算时,船体呈自由悬浮状态[5]。
通过MSC Patran软件[6-8],建立几何模型及有限元模型。在划分网格时,船体外板、甲板、舱壁、肋板等结构采用4节点壳单元离散,纵骨、横梁、扶强材、支柱等构件采用2节点梁单元离散。为了保证有限元计算的精度,船体模型共包括189 103个单元,85 274个节点,全船的有限元模型如图2。

图2 整船有限元计算模型Fig.2 FEM calculation model of the whole ship
为了让模型的质量分布尽可能与设计相吻合,严格按照平台质量、质心报告进行质量调整,并调整模型质心位置与实船的质心位置一致。船体模型中船体材料为低碳钢,弹性模量取2.06×1011N/m2,泊松比为0.3,密度为7 850 kg/m3,按常规方法将船体梁划分成20站,按刘易斯附连水质量计算公式,根据每站水线半宽、实际吃水、浸水面积及三维流动修正系数,算得每站范围内单位长度附连水质量。算得附连水质量后,以质量单元的形式分布在船体湿表面上。
2.2.2 计算结果
应用整船三维有限元模型,得到船体总体振动固有频率,其计算值列于表2,计算图形见图3。
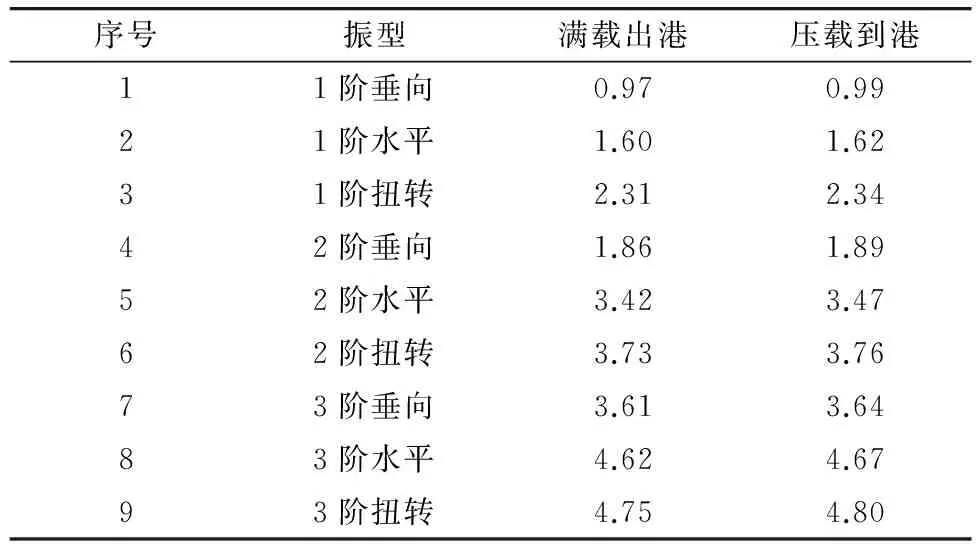
表2 整船模型总振动固有频率计算结果
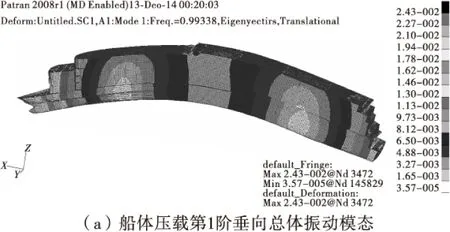
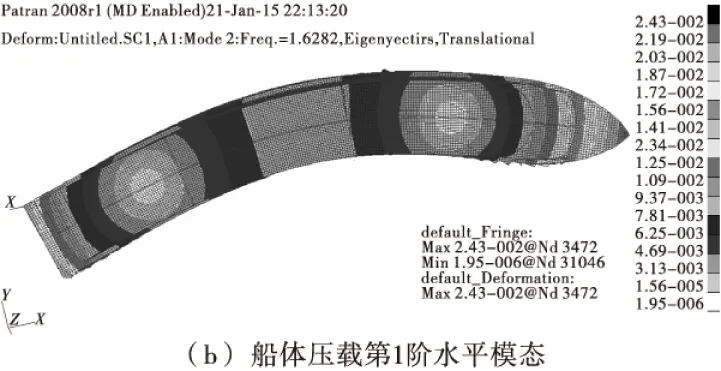
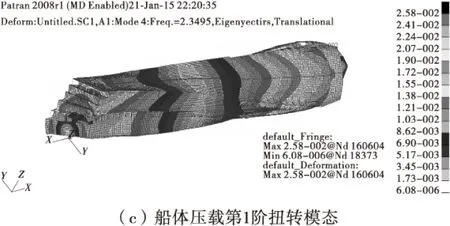



图3 数值模拟结果Fig.3 Numerical simulation results
从图3可以看出,在主机额定工况下,叶频已超过船体垂向总振动前5阶固有频率。因此,螺旋桨叶频能避开共振,不会引起明显的船体垂向总振动。船体总振动计算中,分别采用了船体一维梁模型方法和整船三维有限元方法,两种方法的计算结果差别不是很大,最大偏差为0.19 Hz。由此表明:在船体总振动计算时,在船舶设计初期,应用船体一维梁简化方法也是可行的。
2.3 上层建筑及艉部局部结构振动计算
2.3.1 计算方法
根据船上振动控制指南[9],针对本船的实际情况,船体板架结构固有频率的计算可应用整船三维有限元模型进行计算,而板和板格等局部结构固有频率的计算可采用能量法计算,边界条件为四周自由支持,计算时选取各层甲板的典型构件,如果这些构件能满足频率储备要求,则表示其余类似构件均能满足要求,如果有构件不能满足频率储备要求的,则需要进行结构改进以满足相应的要求[10]。
局部结构计算时甲板上的附加重量取为60.0 kg/m2,舱壁则没有附加重量。
2.3.2 计算模型
在模型中,各层甲板和舱壁采用板单元模拟,其纵桁、横梁等采用梁单元模拟。船体艉部和上层建筑部分的模型及计算见图4。
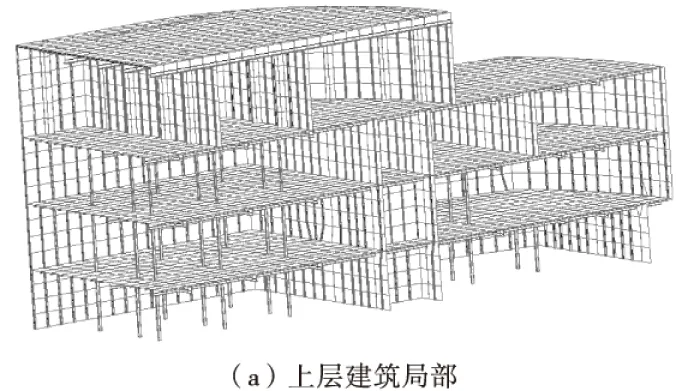
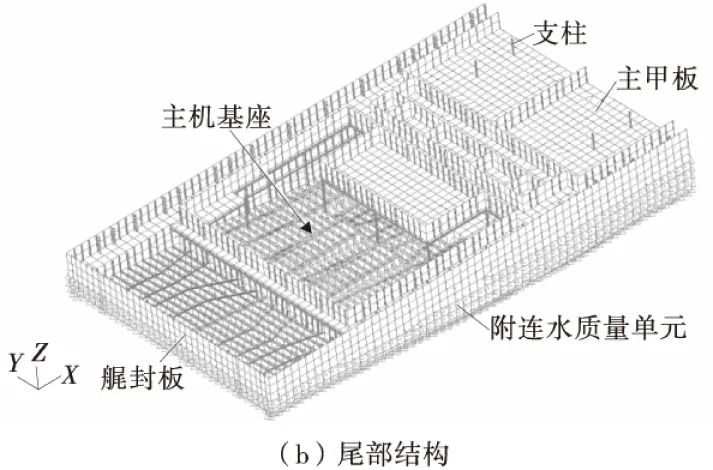
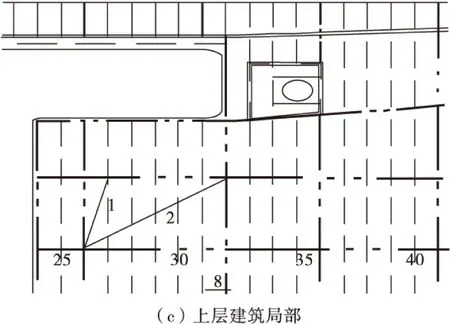
图4 计算模型Fig.4 Calculation model
2.3.3 各层甲板的板和板格固有频率计算结果
部分板及板格计算结果列于表3。
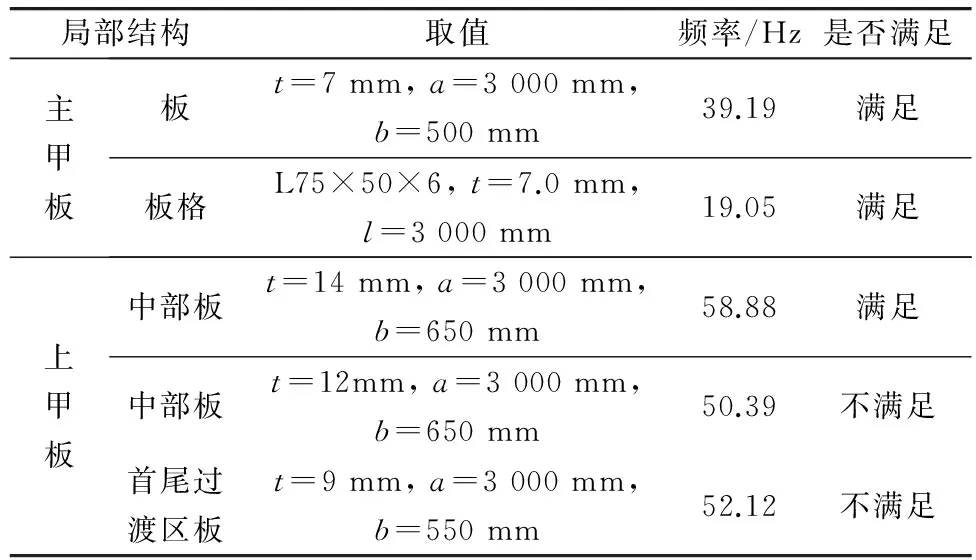
表3 局部结构固有频率计算值
计算结果表明,除上甲板船中、船尾局部区域板的频率和螺旋桨倍叶频率非常接近不能满足频率储备要求外,各层甲板和板格都能满足频率储备要求。
应用整船甲板有限元模型,通过计算,得到各层船体甲板板架固有频率,计算结果表明,各层甲板架均能满足频率储备要求。
2.3.4 强迫响应计算结果
在进行船体振动响应计算时,需考虑阻尼的影响。目前,对于船体阻尼的了解尚不是十分充分,根据《船体振动控制指南》,本计算中阻尼系数近似取为0.015;振动响应计算分别包括了上层建筑和艉部在内的11个部位的纵向、横向和垂向这三个方向的响应值。这11个部位分别是P1,P2点(船体艏部);P3,P4,P10,P11(船体中部);P5,P6,P7,P8,P9(船体后部、机舱底部)等,其振动响应部分计算结果列于表4,强迫响应振动计算位置见图5。
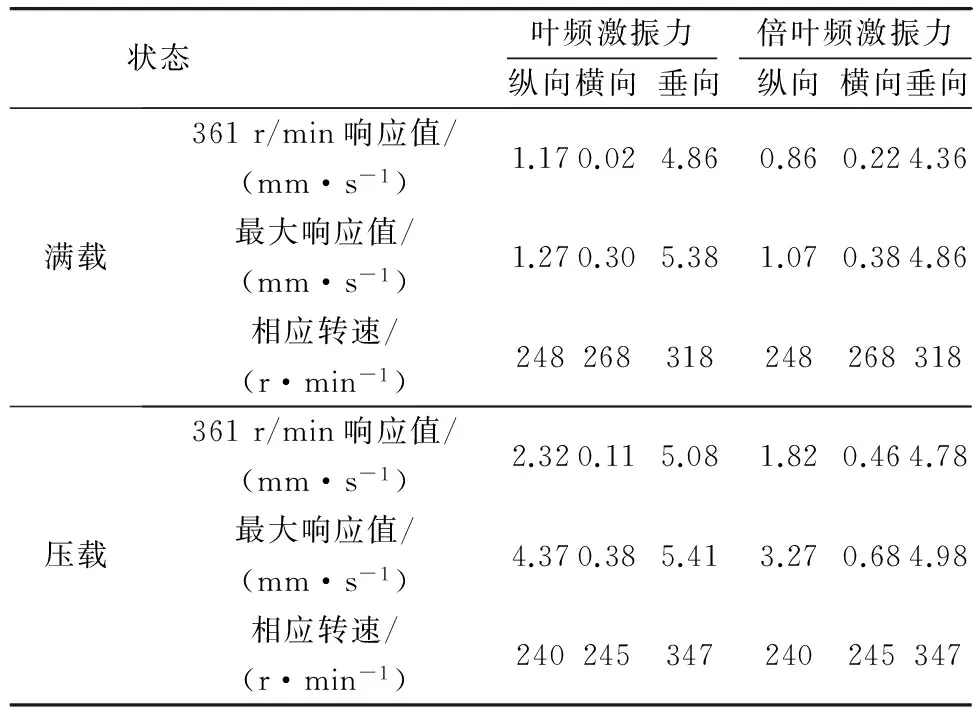
表4 甲板尾部(P6)强迫响应计算结果
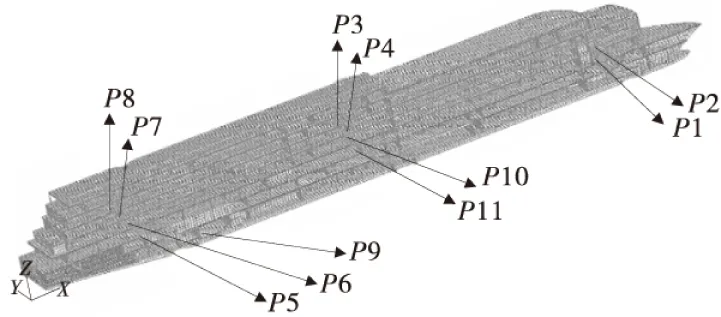
图5 强迫响应计算典型位置Fig.5 Forced response of a typical location map
螺旋桨转速在0~361 r/min之间,在螺旋桨叶频、倍叶频激振力作用下分别在满载和压载工况下对整船模型进行振动响应计算。
从计算结果来看,该船主甲板、上甲板与游步甲板中部及后部局部点位在螺旋桨转速高负荷时候,强迫振动响应已经超过国家振动测试标准。
4 实船总体和局部振动试验
为验证振动预测的准确性及评价船舶的适居性,该游轮在压载工况下进行了实船总体、船体局部结构、机械设备等振动试验。仪器采用30通道动态数据测试仪,分别利用船舶在上水、下水,只开两台螺旋桨,四台螺旋桨全开,从0负荷到满负荷以及停泊抛锚等工况下进行总体和局部振动数据的采集,在每个测量位置,测量的频率范围为1~80 Hz,并且持续测量时间至少为1 min,在优势频率<2 Hz时,测量时间至少持续2 min。每个测量位置都进行了X,Y,Z方向的测量[11]。
4.1 实船总体振动测试数据
实船总体振动测试激振力采用抛锚测试的方法,测试结果见表5。
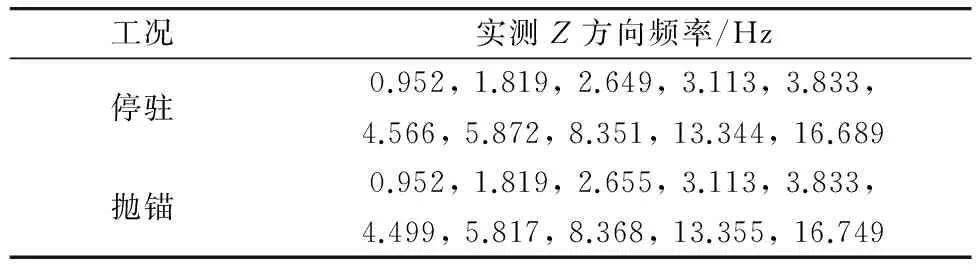
表6 总体振动垂向频率
注:根据实测数据分析得到较多频率成分(见上),因测点较少(只有7个),不易判断频率阶次,尤其是高阶频率识别较困难(高阶振型反弯点更多,测点较少时就无法描绘振型形状)。将实测振型与计算振型相对照,取形状吻合的前三阶频率作为结果(即f1=0.952 Hz,f2=1.819 Hz,f3=3.833 Hz)。
4.2Z方向频率及振型图(图6)
基于测试结果进行了有限元模型的修正,对首尾曲面线型复杂部位,对附连水质量系数进行了进一步的细化,首尾部分,每隔半站计算一次附连水质量。根据模态计算结果,重新检查了个别频率较低的局部模态位置的节点关联及属性分配情况,通过修正模型,有效的减少了个别低频局部模态对船舶总体振型的影响。
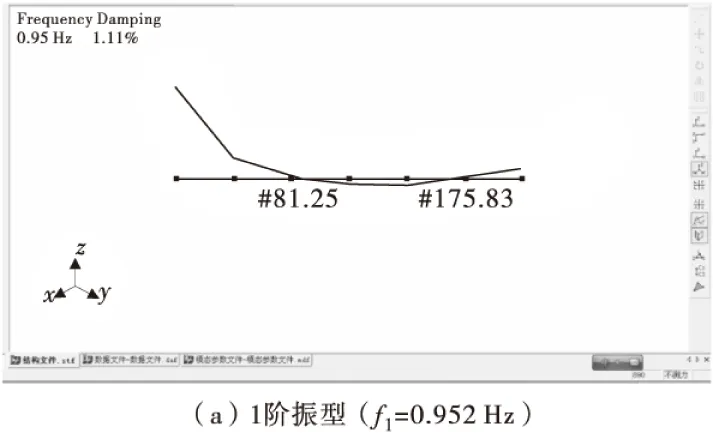
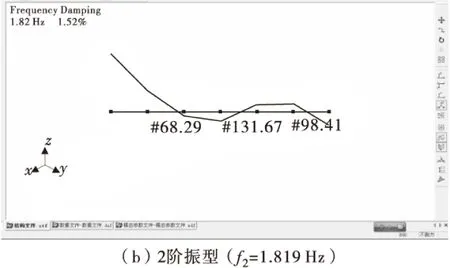
图6 船体总振动试验Fig.6 Ship hull vibration of testing
4.3 局部振动试验
局部振动试验航行方向为上水,选择了本船上甲板餐厅、主甲板尾部尾部,游步甲板客房等位置进行了测量,其部分测试值见表6。

表6 局部振动试验实测加速度有效值
依据 ISO6954规范[12],取测量数据及计算结果的全频域计权均方根值进行对比,从实际测试数据来看,主甲板、上甲板及游步甲板中后部强迫振动响应幅值已经超过国家标准,该结果与我们有限元模型计算结果相似。
5 结 论
1)本船采用电力推进,螺旋桨Z型传动,减少了主机尾轴轴系,实船试验整船振动响应及噪声水平均优于常规推进船型。
2)本船主发电机组设备采用了双层隔振装置后,减振效果明显,试验数据显示经过隔振后,各测点垂向加速度值在100 mm/s2左右,对主体结构激振力可以忽略不计。
3)实船试验及三维数值仿真分析计算显示,船体前5阶固有频率,0.8~7.8 Hz均避开了螺旋桨转速为361.2 r/min时的叶频激振力频率24.08 Hz与倍叶频激振力频率48.16 Hz,没有发生船舶共振。
4)实船试验及局部结构数值仿真分析计算理论计算显示,主甲板、上甲板及游步甲板中后部板及板格固有频率在46~52 Hz之间,与螺旋桨倍叶频率比较,储备不足。
5)实船试验及局部结构数值仿真分析计算理论计算显示,主甲板、上甲板及游步甲板中后部板局部点位强迫响应振动幅值达到300~400 mm/s2,超过了ISO标准。
6)本船激振力主要是四台Z型全回转螺旋桨产生,针对本船局部范围强迫响应值较大,建议今后从三方面着手考虑:①减小螺旋桨激励力,改善船体伴流分布,使之均匀,目前实船尾部采用方尾设计,四台螺旋桨一字型排列,螺旋桨产生的表面力较大,船型与螺旋桨配合流场情况值得进一步研究和探讨;②改进螺旋桨设计参数,减小脉动载荷分量降低激振力,如增大螺旋桨叶片,采用大侧斜桨叶,加大叶梢与船底间隙等;③调整船体局部结构及尺寸等,以增大上层建筑局部板的频率储备。
[1] 史丰荣.船体结构总体振动特性预测技术研究[J].中国造船,2013,54(2):118-123. Shi Fengrong.Global vibration analysis of hull structure [J].Shipbuilding of China,2013,54(2):118-123.
[2] 申俊敏,张艳聪,田波.钢筋网对道路混凝土振动的阻隔及对策[J].重庆交通大学学报:自然科学版,2012,31(2):247-251. Shen Junmin,Zhang Yancong,Tian Bo.Barrier and countermeasures of reinforced mesh on pavement concrete vibration [J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(2):247-251.
[3] 金咸定,夏利娟.船体振动学[M].上海:上海交通大学出版社,2011:34-40. Jin Xianding,Xia Lijuan.Hull Vibration [M].Shanghai:Shanghai Jiaotong University Press,2011:34-40.
[4] 何友声,王国强.螺旋桨激振力[M].上海:上海交通大学出版社,1987:56-60. HeYousheng,Wang Guoqiang.Propeller Exciting Force [M].Shanghai:Shanghai Jiaotong University Press,1987:56-60.
[5] 吴嘉蒙.2750TEU集装箱船的全船总振动评估[J].船舶,2008(2):45-50. Wu Jiameng.Evaluation on global vibration analysis on a 2750TEU container vessel [J].Ship & Boat,2008(2):45-50.
[6] ABS.Guidance Notes on Ship Vibration [S].New York:American Bureau of Shipping,2006.
[7] MSC Software Corporation.PCL and Customization [M].Geneva Switzerland:Mediterranean Shipping Company,2003:67-73.
[8] MSC Software Corporation.PCL Reference Manual [M].Geneva Switzerland:Mediterranean Shipping Company,2003:80-85.
[9] GB 026—2000船上振动控制指南[S].北京:人民交通出版社,2000. GB 026—2000 Vibration Control Board Guide [S].Beijing:China Communications Press,2000.
[10] 吴嘉蒙,陈曙梅.2750 TEU集装箱船的局部振动评估[J].船舶,2008(5):10-16. Wu Jiameng,Chen Shumei.Evaluations on local vibration analysis on a 2750 TEU container vessel [J].Ship & Boat,2008(5):10-16.
[11] 付长虎,刘红光,陆森林.客车车身的有限元模态及谐响应分析[J].重庆交通大学学报:自然科学版,2013,32(6):1267-1269. Fu Changhu,Liu Hongguang,Lu Senglin.Finite element modal and harmonic analysis of bus body [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(6):1267-1269.
[12] International Standard ISO 6954.Mechanical Vibration and Shock- Guidelines for Overall Evaluation of Vibration in Merchant Ships [S].Geneva Switzerland:IEC Central Office,1984.
Numerical Simulation and Experimental Research on River Electric Propulsion Ship Vibration
Yang Jingdong, Wang Zhixiang, Sun Yonggan, Wang Hongmei
(School of Shipping & Marine Engineering,Chongqing Jiaotong University, Chongqing 400074, China)
For the stern area harmful vibration problems of the first river electric propulsion luxury cruise ship, the simulation calculation for ship whole and local structure was carried out by MSC PATRAN software; the overall structure and local excitation source, vibration mode and natural frequency were studied. Comparative analysis was carried out between the experimental data and the measured data, which verified the reliability of the theoretical analysis and numerical simulation. Furthermore, the causes in terms of vibration problems were summarized, and the corresponding ship vibration optimization measures were put forward.
ship engineering; ship harmful vibration; simulation analysis and calculation; ship vibration reduction
10.3969/j.issn.1674-0696.2015.05.35
2014-11-05;
2015-01-24
重庆市科技攻关计划项目(cstc2012gg-yyjsB70002)
杨敬东(1970—),男,重庆人,高级工程师,硕士,主要从事现代造船技术及船体结构优化方面的研究。E-mail:274245970@qq.com。
U661.43
A
1674-0696(2015)05-175-06
